Movimento Uniformemente Variado (MUV) – Resolução

Resolução comentada dos exercícios de vestibulares das questões de Física sobre

Movimento Uniformemente Variado (MUV)

01- Quando t=0 a distância entre eles é de 32m  —  até t=4s, quando terminou a desaceleração o veículo A se deslocou   —  ΔS_A=área do trapézio=(30 + 15).4/2   —  ΔS_A=90m  —  no mesmo intervalo de tempo o veículo B se deslocou  —  ΔS_B=área do retângulo=4.15=60m  —  a distância entre eles antes era de   —  ΔS_a=32m (dado do exercício)  —  depois, ΔS_d=(90 – 60)=30m  —  a distância entre eles no final da frenagem será de d=32 – 30=2m  —  R- B. 

02- Primeira situação  —  cálculo da aceleração do carro com a pista seca  —  V²=Vo² + 2.a.∆S  —  0² = 10² + 2.a.5  —  a=-10ms2  —  cálculo da aceleração do carro com a pista molhada  —  V²=Vo² + 2.a.∆S  —  0² = 10² + 2.a.6  —  a=-100/12=-25/3 ms²  —  segunda situação  —  cálculo da distância percorrida com a pista seca  —  V²=Vo² + 2.a.∆S  —  0² = 30² + 2.(-10). ∆S  —  ∆S =45m  —  cálculo da distância percorrida com a pista molhada  —  V²=Vo²+ 2.a.∆S  —  0² = 30² + 2.(-25/3).∆S  —  ∆S=54m  —  distância percorrida a mais até parar  —  d=54 – 45=9m  —  R- D.

03- Observe na expressão D=K.V², onde K é constante e, nela você observa que a velocidade V é diretamente proporcional ao quadrado da velocidade  —  assim, se a velocidade dobra passando de 80kmh para 160kmh, a distância percorrida pelo carro até parar fica 2²=4 vezes maior  —  R- C.

04-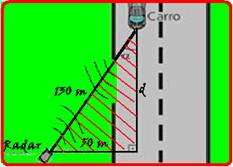  

Observe no esquema abaixo no triângulo hachurado que  —  130²=50² + d²  —  d²=14400  —  d=120  —  cosα=cateto adjacente/hipotenusa=120/130  —  72=V_r.120/130  —  V_r=78km/h  —  R- C.

05-  Calculando o espaço percorrido entre 0 e 10s pela área  —  móvel A  —  ΔS_A=(B + b).h/2=(45 + 30).10/2  —  ΔS_A=375m (deslocou 375m no sentido positivo da trajetória)  —  móvel B  —  ΔS_B=(-10 – 30).10/2  —  ΔS_B=-200m (deslocou 200m no sentido negativo da trajetória)  —  d=375 + 200  —  d=575m  —  cálculo da aceleração escalar de cada móvel   —  a_A=∆V_A/∆t  —  a_A=(45 – 30)/(10 – 0)  —  a_A=1,5m/s²  —  a_B=(-30 – (-10)/(10 – 0)  —  a_B= -2m/s²  — S_A=So_A + 30t + 0,75t²  —  S_B=So_B – 10t – t²  —  supondo S_oA=0 e fazendo t=10s no encontro onde você iguala as equações  —  30(10) + 0,75(10)² = S_oB – 10(10) – (10)²  —  375 = So_B – 200  —  So_B = 575 m, que é a distância inicial entre os móveis, pois supusemos o móvel A partindo da origem.

R- A

06- Ela vai (ida) pára e volta  —  se, na ida ela tem velocidade de 50m/s, na volta deverá ter velocidade de -50m/s  —   

na ida, V_o=50m/s e V=0, ela demorou  — V=V_o + at  —  0=50 – 0,2t  —  t=250s (na ida)  —  na volta  —  V_o=0 e V=-50m/s  —  V=Vo + at  —  -50=0 -0,2t  —  t=250s (na volta)  —  t_pedido=t_ida + t_volta  —  t_pedido=250 + 250=500s  —t=500s  —  R- A.

07- Cálculo da distância percorrida pelo predador  —  entre 0 e 4s  —  acelerado com a=(54/3,6 – 0)/(4 – 0)=3,75m/s²  —  ΔS₁=V_o.t + at²/2=0.4 +3,75.16/2  —  ΔS₁=90m  —  entre 4s e 10s é um MU com V=15ms  —  V= ΔS/Δt  —  15= ΔS₂/6  —  ΔS₂=90m  — ΔS_predador=90 + 90  —  ΔS_predador=180m  —  cálculo da distância percorrida pela presa  —  entre 0 e 5s  —  acelerado com a=(12 – 0)/(5 – 0)=2,4m/s²  —  ΔS₁=Vot + at²/2=0.5 +2,4.25/2  —  ΔS₁=30m  —  entre 5s e 10=14s é um MU com V=12ms  —  V= ΔS/Δt  —  12= ΔS₂/9  —  ΔS₂=108m  — ΔS_presa=30 + 108  —  ΔS_presa=138m  —  portanto para o predador obter sucesso, a distância inicial máxima entre ele e a presa deverá ser de  —  d=180 – 138  —  d=42m  —  R- C.

08- a) Equação de Torricelli  —  V²=V_o² + 2.a.∆S  —  veículo A  —  V_A²=20² + 2.4.150  —  V_A=40m/s  —  veículo B  —  V_B²=15² + 2.6.150  —  V_B=45m/s.  

b) Cálculo do tempo que cada móvel demora para percorrer os 150m  —   ∆S_A=V_oA.t + a_A.t²/2  —  150=40t + 4t²/2  — 

t₁=-15s (anulado) e t_A=5s  —  ∆S_B=V_oB.t + a_B.t²/2  —  150=45t + 6t²/2  —  t₁=-30s (anulado) e t_B=5s  — após as curvas os dois veículos se moveram durante 5s  —  nesses t=5s o móvel A percorreu   S_A=S_oA + V_oA.t + a_A.t²/2=0 + 40.5 + 4.25/2=250m  —  S_A=300m  —  S_B=S_oB + V_oB.t + a_B.t²/2=0 + 45.5 + 6.25/2=m  —  S_A=300m  —  observe na figura que a projeção de S_B=300m sobre a horizontal fornece S’_B=S_B.cos60^o=300.0,5=150m  —  agora, aplicando Pitágoras você calcula a distância d pedida  —  d²=250² + 150²=62500 + 22500=85000  —  d=291,54m.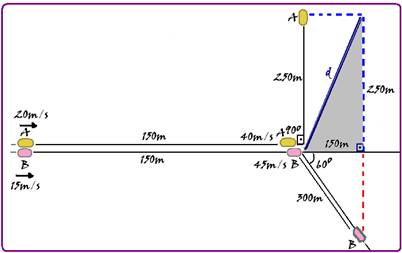

09- Cálculo da aceleração  —  V=V_o + at  —  0=30 + a.6  —  a=-5m/s²  —  com essa aceleração sua velocidade deve ser reduzida de V_o=30m/s para V=10m/s em  —  30=10 – 5t  —  t=4s e, nesse tempo ele deve percorrer ΔS= V_o.t + at²/2=30.4 – 5.16/2=80m ou com Torricelli  —  V²=Vo² + 2a ΔS  —  100=900 – 2.5. ΔS  —  ΔS=80m  —  R- C.

10- S_o=0  —  V_o=0  —  S=S_o + V_o.t + at²/2  —  s=a.t²/2  —  como a é constante, S é diretamente proporcional a t², ou seja, aumenta proporcionalmente com o quadrado do tempo  —  R- C.

11-  a) Até começar a frear ele deve demorar   —  t=2,2 – 0,5  —  t=1,7s  para sua velocidade passar de V_o=12m/s até V=0  —  V= V_o + a.t  —  0=12 + a.1,7  —  a= -7,1m/s².

b) Até começar a frear ele percorreu ΔS₁ com velocidade constante de V=12m/s durante t=0,5s  —  V= ΔS₁/ Δt  —  12= ΔS₁/0,5  —  ΔS₁=6m  —  para passar pelo cruzamento sem ser multado ele deve percorrer ΔS=30 – 6=24m em t=2,2 – 0,5=1,7s  —  ΔS=V_o.t + a.t²/2  —  24=12.1,7 + a.(1,7)²/2  —  24=20,4 + a.3/2  —  a=2,4m/s^2.

12- 

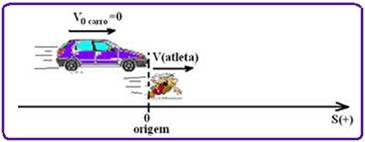
Baseado na figura abaixo deduz-se a equação de cada móvel  —  carro  — MUV  —  S_c=So + V_ot + at²/2= 0 + 0 +2t²/2  —  S_c=t²  —  e do atleta  —  MU    —  S_at=S_o + V.t  —  S_at= 0 + V.t  —  S_at=V.t  —  se o atleta se mantém na frente do carro por t=3s  —  S_at = S_c, quando t=3s  —  V.t=t²  —  V.3 = 3²  —  V=3m/s  —  R- B.

13-  A velocidade inicial V_o é a mesma para os dois veículos V_o=108km/h/3,6=30m/s  —  deduzindo as

equações de   cada móvel de acordo com o esquema  —  V=V’=V_o=30m/s  —  equação de um ponto no pára-choque dianteiro do caminhão  — S_caminhão=S_o + V_o.t + at²/2=0 + 30.t – 2.t²/2  —  S_caminhão=30t – 1t²  —  equação de um ponto do pára-choque traseiro do carro  —  S_carro= S_o + V_o.t + at²/2= d + 30t – 3t²/2  — S_carro=d + 30t -1,5t²  —  o tempo que demorou para parar o caminhão (V=0) vale  —  V_caminhão=V_o – 2t  —  0=30 – 2t  —  t_caminhão=15s  —  até parar o caminhão percorre  —  S_caminhão=30t – 1t²=30.15 – 1.(15)²=450 – 225  —  S_caminhão=225m  —  tempo que o carro demora para parar  —  V_carro=V_o – at  —  0=30 – 3t  —  t=10s  —  distância que o carro percorre até parar  —  S_carro=d + 30t -1,5t²=d + 30.10 – 1,5.100  —  S_carro=d + 150  — no encontro  —  S_carro = S_caminhão  —  d + 150=225  —  d=75m  —  R- B.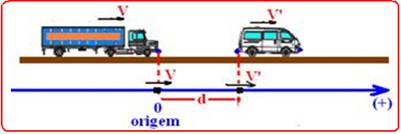

14-  a) Como A e Z se deslocam em sentidos opostos, o módulo da aceleração relativa entre eles é a = 6 m/s²  —  como

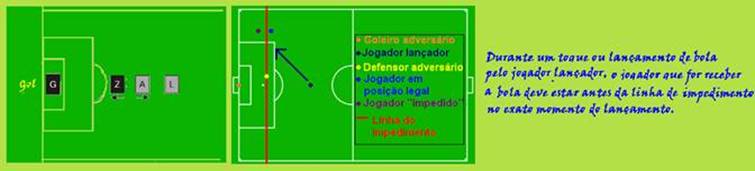 suas acelerações tem mesmo módulo, cada jogador percorre até o encontro metade da distância que os separa, ou seja, d= 6 m, distância que percorre em  —  S= S_o + V_o.t + a.t²/2  —  d=0 + 0 =at²/2  —  6=3t²/2  — t=2s.

b) Cada jogador tem velocidade constante de 6 m/s, em sentidos opostos  —  no intervalo de 0,1 s, o deslocamento de cada um é ∆S = v.∆t = 6 (0,1) = 0,6 m  —  ∆S=6m,  portanto, no momento do lançamento, a distância mínima (dmin) entre eles tem que ser  —  d_min= 2.(0,6)  —  d_min= 1,2 m  —  você também poderia utilizar a velocidade relativa que, em sentidos contrários é a soma das velocidades de cada um  —  Vr=6 + 6=12  —  Vr=12m/s  —  d=Vr.Δt=12.(0,1)  — d=1,2m.

15- 

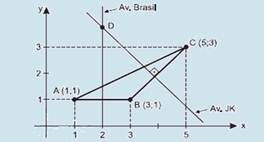
Observe a figura abaixo  —  a catedral se encontra no ponto A(1;1), a prefeitura no ponto B (3;1) e a câmara de vereadores  no ponto C (5;3)  —  observe que AB=2 e AC2=(5 – 1)² + (3 – 1)²  —  AC=2√5  —  como AB=500m  —  AC=500√5m    R- A.

16- Observe na figura abaixo que entre o início da ultrapassagem e o final da mesma um ponto P

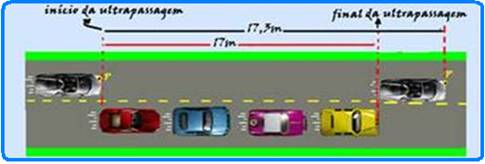
fixo, por exemplo, no farol do carro que está ultrapassando, percorreu ∆S=17 + 3=17,3m  —  observe também que tanto os carros da fileira como o que está ultrapassando possuem a mesma velocidade, então a velocidade relativa entre eles é nula e, você pode considerar nesse estudo que inicialmente todos estavam em repouso  —  assim, o ponto P com velocidade inicial V_o=0 inicia seu movimento para ultrapassar uma distância fixa de ∆S=17,3m, com aceleração a, demorando t=4s para isso  —  ∆S=V_o.t + a.t²/2=  —  17,3 = 0.4 + a.4²/2  —  a=17,3/8=2,16m/s²  —  cálculo da velocidade no final da ultrapassagem  —  V=V_o + a.t=0 + 2,16.4  —  V=8,65m/s  —  essa é a velocidade supondo os carros parados mas, na realidade, eles têm velocidade de 90km/h=25m/s  —  V_real=25 + 8,65=33,65m/s. 

R- C.

17-  Entre 0 e 10s  —  V_o=0  —  V=V_o + at=0 + 1.10=10m/s  —  entre 10s e 20s  —  V_o=10m/s  —  V=V_o + at=10 + 2.10=30m/s  —  entre 20s e 50s  —  a aceleração é nula e a velocidade constante de 30m/s  —  entre 50s e t ele freia e pára com sua velocidade variando de 30m/s para 0  —  V=V_o + at  —  0=30 -1.t —  t=30s  —  t_f=50 + 30=80s

Construindo o gráfico Vxt, cuja área entre a reta representativa e o eixo t fornece o deslocamento (no

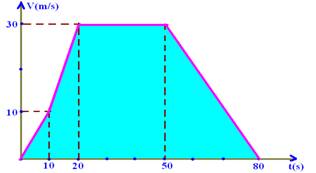
caso, distância)entre as duas estações  —  ΔS_total=soma das áreas=10.10/2 + (30 + 10).10/2 + 30.30 + 30.30/2  — ΔS_total=1.600m  —  R- A

18- 

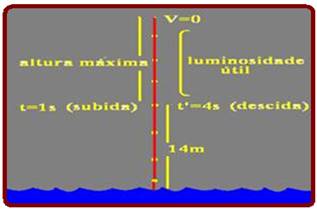
Cálculo dos instantes em que ele passa pela altura de 14m, ou seja, S=14m  —  S=10 + 5t – t²  —  14=10 +5t – t²  — 

t² – 5t + 4=0 —  t=1s (subida e t’=4s (descida)  —  ele estará acima de 14m (luminosidade útil) entre os instantes 1s e 4s  —  Δt=4 – 1=3s   —   R- A.

 

19-Se você fixar um ponto P no início da locomotiva , quando P começar a passar diante do observador (marco inicial 0), você terá velocidade inicial V_o e t_o=0, e quando a locomotiva terminar de passar pelo observador P estará a 24m de 0 no instante t=4s (figura I).

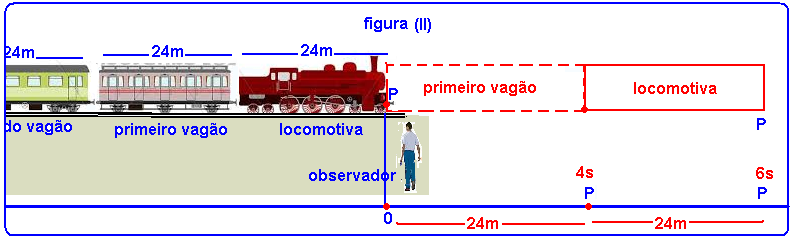
Pelo enunciado, quando o primeiro vagão terminar de passar pelo observador o ponto P estará a 48m de 0 e o instante será t=4 + 2 = 6s (figura II)

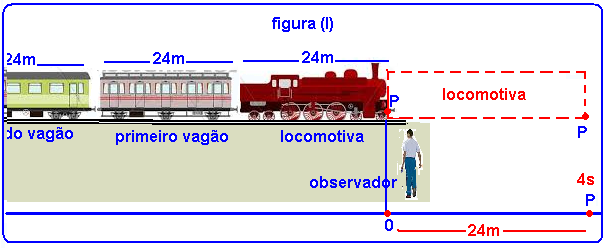
Na figura I, quando t=4s o ponto P, com velocidade inicial V_o e aceleração a, percorreu ΔS=24m —

ΔS= V_ot + at²/2 — 24 = v_o.4 + a.4²/2 — 24 = 4V_o + 8a — 6 = V_o + 2a — V_o= 6 – 2a (1).

Na figura II, quando t=6s o ponto P, com velocidade inicial V_o e aceleração a, percorreu ΔS=48m —

ΔS= V_ot + at²/2 — 48 = V_o.6 + a.6²/2 — 48 = 6V_o + 18a — 8 = V_o + 3a (2).

(1) em (2) — 8=6 – 2a + 3a — a=2m/s² (aceleração da composição).

V­_o= 6 – 2.2 — V_o=2m/s (velocidade inicial do ponto P).

Quando o primeiro vagão começa a passar diante do observador o ponto P está na posição 24m e o instante é t=4s — V=V_o + at=2 + 2.4=10m/sx3,6=36km/h.

R- D

20- Nos primeiros 50m ele partiu do repouso V_o=0, acelerou com aceleração a e terminou os 50m com velocidade V₁: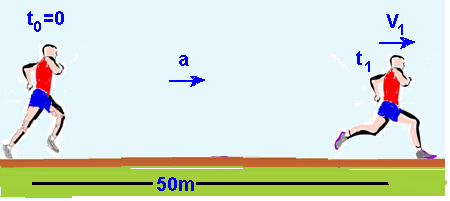

ΔS=V_ot + at²/2 — 50=0.t₁ + a.t₁²/2 — 100=at₁² — t₁=10/√a (I).

V=V_o + at — V₁ = 0 + a.t₁ — V₁ = a. 10/√a — V₁.√a = 10a — V₁².a = 100a² — v₁² = 100√a —

√a = V₁/10 (II).

(II) em (I) — t₁ = 10/V₁/10 — t₁=100/V₁ (III).

Os últimos 50m ele percorre com velocidade constante de valor V₁ num intervalo de tempo t₂:

V= ΔS/Δt — V₁=50/t₂ — t₂=50/V₁.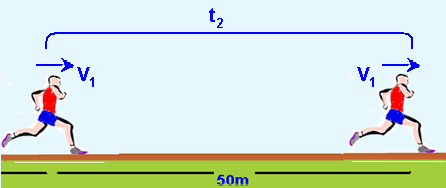

Como ele demorou 10s para efetuar todo o percurso você terá que t₁ + t₂ = 10 — (III) + (IV) = 10 — 100/V₁ + 50/V₁ = 10 — 150 = 10V₁ — V₁=15m/s.

A aceleração a é calculada substituindo V₁=15m/s em (II) — √a = V₁/10 — √a = 15/10=1,5 — a=1,5² — a=2,25m/s².

Tempo t₁ — substituindo V₁=15ms em (III) — t₁=100/15 — t₁=6,7s — tempo t₂ — t₁ + t₂=10 —

6,7 + t₂ = 10 — t₂=3,33s.

 

Voltar para os exercícios