LANÇAMENTO OBLÍQUO E LANÇAMENTO HORIZONTAL
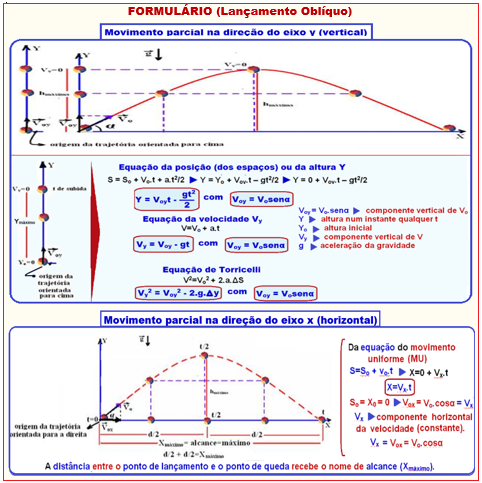
Exercícios de vestibulares com resoluções comentadas sobre
Lançamento Oblíquo e Lançamento Horizontal
01-(CEFET-CE)
Um caminhão se desloca em movimento retilíneo e horizontal, com velocidade constante de 20m/s. Sobre sua carroceria, está um canhão, postado para tiros verticais, conforme indica a figura.
A origem do sistema de coordenadas coincide com a boca do canhão e, no instante t = 0, ele dispara um projétil, com velocidade de 80m/s. Despreze a resistência do ar e considere g = 10 m/s2.
Determine o deslocamento horizontal do projétil, até ele retornar à altura de lançamento, em relação:
a) ao caminhão;
b) ao solo.
02-(UFF-RJ)
Após um ataque frustrado do time adversário, o goleiro se prepara para lançar a bola e armar um contra ataque.
Para dificultar a recuperação da defesa adversária, a bola deve chegar aos pés de um atacante no menor tempo possível.
O goleiro vai chutar a bola, imprimindo sempre a mesma velocidade, e deve controlar apenas o ângulo de lançamento.
A figura mostra as duas trajetórias possíveis da bola num certo momento da partida.
Assinale a alternativa que expressa se é possível ou não determinar qual destes dois jogadores receberia bola no menor tempo. Despreze o efeito da resistência do ar.
(A) Sim, é possível, e o jogador mais próximo receberia a bola no menor tempo.
(B) Sim, é possível, e o jogador mais distante receberia a bola no menor tempo.
(C) Os dois jogadores receberiam a bola em tempos iguais.
(D) Não, pois é necessário conhecer os valores da velocidade inicial e dos ângulos de lançamento.
(E) Não, pois é necessário conhecer o valor da velocidade inicial.
(UERJ-RJ)
Este enunciado refere-se às questões de números 03 e 04.
Um trem em alta velocidade desloca-se ao longo de um trecho retilíneo a uma velocidade constante de 108 km/h.
Um passageiro em repouso arremessa horizontalmente ao piso do vagão, de uma altura de 1 m, na mesma direção e sentido do deslocamento do trem, uma bola de borracha que atinge esse piso a uma distância de 5 m do ponto de arremesso.
03-(UERJ-RJ)
Se a bola fosse arremessada na mesma direção, mas em sentido oposto ao do deslocamento do trem, a distância, em metros, entre o ponto em que a bola atinge o piso e o ponto de arremesso seria igual a:
( 04-(UERJ-RJ)
O intervalo de tempo, em segundos, que a bola leva para atingir o piso é cerca de:
05-(UFC-CE)
Uma partícula pontual é lançada de um plano inclinado conforme esquematizado na figura a seguir. O plano tem um ângulo de inclinação θ em relação à horizontal, e a partícula é lançada, com velocidade de módulo v, numa direção que forma um ângulo de inclinação α em relação ao plano inclinado.
Despreze qualquer efeito da resistência do ar.
Considere que a aceleração da gravidade local é constante (módulo igual a g, direção vertical, sentido para baixo).
a) Considerando o eixo x na horizontal, o eixo y na vertical e a origem do sistema de coordenadas cartesianas no ponto de lançamento, determine as equações horárias das coordenadas da partícula, assumindo que o tempo é contado a partir do instante de lançamento.
b) Determine a equação da trajetória da partícula no sistema de coordenadas definido no item (a).
06-(UNICAMP-SP)
Uma bola de tênis rebatida numa das extremidades da quadra descreve a trajetória representada na figura a seguir, atingindo o chão na outra extremidade da quadra.
O comprimento da quadra é de 24 m.
a) Calcule o tempo de vôo da bola, antes de atingir o chão. Desconsidere a resistência do ar nesse caso.
b) Qual é a velocidade horizontal da bola no caso acima?
07-(CEFET-CE)
Uma roda de raio R rola uniformemente, sem escorregar, ao longo de uma superfície horizontal.
Do ponto A da roda se desprende uma gota de barro, como mostra a figurar.
Com que velocidade v deve se deslocar a roda, se a gota, depois de lançada ao espaço, volta a cair sobre o mesmo ponto da roda após efetuar uma volta? Considere desprezível a resistência do ar.
08-(PUC-SP)
O esquema apresenta uma correia que transporta minério, lançando-o no recipiente R.
A velocidade da correia é constante. Para que todo o minério caia dentro do recipiente, a velocidade v da correia, dada em m/s, deve satisfazer a desigualdade:
a) 2 < v < 3
b) 2 < v < 5
c) 1 < v < 3
d) 1 < v < 4
e) 1 < v < 5
09-(UERJ-RJ)
Um avião, em trajetória retilínea paralela à superfície horizontal do solo, sobrevoa uma região com
velocidade constante igual a 360 km/h.
Três pequenas caixas são largadas, com velocidade inicial nula, de um compartimento na base do avião, uma a uma, a intervalos regulares iguais a 1 segundo.
Desprezando-se os efeitos do ar no movimento de queda das caixas, determine as distâncias entre os respectivos pontos de impacto das caixas no solo.
10-(FISICA E VESTIBULAR)
Se, com um arco e flecha, você mirar a flecha diretamente para o alvo fixo (figura 1), a flecha atingirá o ponto visado?
Por outro lado, se você mirar a flecha diretamente para uma maçã em queda livre (figura 2), a flecha a atingirá?
Justifique.
11-(UFJF-MG)
Durante uma partida de futebol, um jogador, percebendo que o goleiro do time adversário está longe do gol, resolve tentar um chute de longa distância (vide figura).
O jogador se encontra a 40 m do goleiro.
O vetor velocidade inicial da bola tem módulo Vo= 26 m/s e faz um ângulo de 25° com a horizontal, como mostra a figura a seguir.
Desprezando a resistência do ar, considerando a bola pontual e usando cos 25° = 0,91, sen 25° = 0,42 e g=10m/s2:
a) Faça o diagrama de forças sobre a bola num ponto qualquer da trajetória durante o seu vôo, após ter sido chutada. Identifique a(s) força(s).
b) Saltando com os braços esticados, o goleiro pode atingir a altura de 3,0 m. Ele consegue tocar a bola quando ela passa sobre ele? Justifique.
c) Se a bola passar pelo goleiro, ela atravessará a linha de gol a uma altura de 1,5 m do chão.
A que distância o jogador se encontrava da linha de gol, quando chutou a bola? (Nota: a linha de gol está atrás do goleiro).
12-(PUC-SP)
Dois amigos, Berstáquio e Protásio, distam de 25,5m.
Berstáquio lança obliquamente uma bola para Protásio que, partindo do repouso, desloca-se ao encontro da bola para segurá-la.
No instante do lançamento, a direção da bola lançada por Berstáquio formava um ângulo θ com a horizontal, o que permitiu que ela alcançasse, em relação ao ponto de lançamento, a altura máxima de 11,25m e uma velocidade de 8m/s nessa posição.
Desprezando o atrito da bola com o ar e adotando g = 10m/s2, podemos afirmar que a aceleração de Protásio, suposta constante, para que ele consiga pegar a bola no mesmo nível do lançamento
deve ser de
13-(FUVEST-SP) Um motociclista de MotoCross, move-se com velocidade V = 10 m/s, sobre uma superfície plana, até atingir uma rampa (em A), inclinada de 45o com a horizontal, como indicado na figura.
A trajetória do motociclista deverá atingir novamente a rampa a uma distância horizontal D (D=H), do ponto A, aproximadamente igual a: (g=10m/s2)
a) 20m
b) 15m
c) 10m
d) 7,5m
e) 5m
14-(Olimpíada Brasileira de Física)
Dois rapazes brincam de tênis na praia.
Um deles dá uma raquetada na bola a 2,45 m de altura e esta sai horizontalmente com velocidade de 72 km/h.
Qual deve ser a velocidade mínima do outro rapaz, situado inicialmente 20,3 m à frente do primeiro, para que consiga aparar a bola antes que ela bata na areia? (Adote g = 10 m/s2).
15-(FISICAEVESTIBULAR)
Um projétil 1 se move em linha reta, a 1125m do solo, com velocidade horizontal V =1080 km/h
No solo existe um projétil 2 que é disparado com velocidade de 540 km/h, exatamente quando o projétil 1 está passando sobre ele na mesma vertical. Despreze a resistência do ar, as dimensões dos dois projéteis e considere g = 10 m/s2.
a) Calcule o ângulo com que deve ser lançado o projétil 2 com o solo para que atinja o projétil 1.
b) Localize o ponto do impacto entre os dois projéteis num plano de coordenadas cartesianas com a origem no ponto de lançamento do projétil 2.
16-(UFMG-MG)
Um cano de irrigação, enterrado no solo, ejeta água a uma taxa de 15 litros por minuto com uma velocidade de 10 m/s.
A saída do cano é apontada para cima fazendo um ângulo de 30° com o solo, como mostra a figura. Despreze a resistência do ar e considere g = 10 m/s2, sen 30° = 0,50 e cos 30° = 0,87.
Calcule quantos litros de água estarão no ar na situação em que o jato d’água é contínuo do cano ao solo.
17-(UFG-GO)
Os quatro blocos, representados na figura com suas respectivas massas, são abandonados em um plano inclinado que não apresenta atrito e termina voltado para a direção horizontal.
Os blocos, ao deixarem a plataforma, descrevem trajetórias parabólicas em queda livre e alcançam o solo, formando, da esquerda para a direita, a seqüência:
a) m; 5m; 2m; 3m
b) m; 2m; 3m; 5m
c) 3m; 2m; 5m; m
d) 3m; 5m; m; 2m
e) 5m; 3m; 2m; m
18-(PFB)
Uma bola de golfe é jogada do alto de uma escada com velocidade horizontal de 3m/s.
Cada degrau tem 30cm de comprimento (profundidade, passo)) e 18 cm de altura (espelho).
Despreze a resistência do ar, considere g = 10 m/s2 e determine que degrau a bola tocará primeiro.
19-(PUC-RJ)
Em um campeonato recente de vôo de precisão, os pilotos de avião deveriam “atirar” um saco de areia dentro de um alvo localizado no solo.
Supondo que o avião voe horizontalmente a 500 m de altitude com uma velocidade de 144 km/h e que o saco é deixado cair do avião, ou seja, no instante do “tiro” a componente vertical do vetor velocidade é zero, podemos afirmar que: (Considere a aceleração da gravidade g = 10 m/s2 e despreze a resistência do ar)
a) o saco deve ser lançado quando o avião se encontra a 100 m do alvo;
b) o saco deve ser lançado quando o avião se encontra a 200 m do alvo;
c) o saco deve ser lançado quando o avião se encontra a 300 m do alvo;
d) o saco deve ser lançado quando o avião se encontra a 400 m do alvo;
e) o saco deve ser lançado quando o avião se encontra a 500 m do alvo.
20-(UFAM-AM)
Uma bola de futebol com 450 g de massa, inicialmente em repouso, é chutada obliquamente para cima com velocidade inicial de 20m/s. A bola atinge altura máxima de 10m e atinge uma parede vertical 2s após o chute.
Desprezando a resistência do ar,
podemos afirmar que a distância do ponto de lançamento da bola até a parede é aproximadamente igual a:
a) 40m
b) 28m
c) 20m
d) 10m
e) 14m
21-(UPF-RS)
Considere um vagão deslocando-se em uma trajetória retilínea com velocidade constante e igual a 5 m/s.
Um observador, A,dentro dele, lança uma pedra verticalmente para cima.
Um outro observador, B, do lado de fora do vagão e em repouso em relação à Terra, observa o vagão passar.
Sendo VA e VB , respectivamente, as velocidades da pedra no ponto mais alto de sua trajetória em relação a cada observador, pode-se concluir que:
a) VA = 0 e VB = 0
b) VA = 0 e VB = 5 m/s
c) VA = 5 m/s e VB = 0
d) VA = 5 m/s e VB = 5m/s
e) VA = 0 e VB = 10 m/s
22-(UEFS-BA)
Um goleiro chuta uma bola, que se encontra parada no gramado, para um jogador situado a 57,0m da
posição do goleiro.
A bola é lançada com velocidade de 20,0m/s, fazendo um ângulo de 45° com o plano horizontal.
Desprezando-se a resistência do ar, considerando-se o módulo da aceleração da gravidade local igual a 10,0m/s2 e sabendo-se que sen45° = cos45° = √2/2, o módulo da velocidade do jogador para alcançar a bola, no instante em que ela toca o gramado, em m/s, deve ser de, aproximadamente,
A) 4,0 B) 5,0 C) 6,0 D) 7,0 E) 8,0