Hidrostática – Resolução
Resoluções comentadas dos exercícios de vestibulares sobre
Hidrostática
01-
Aplicando o teorema de Stevin — pressão hidrostática devido apenas à altura da coluna de água — P=dágua.g.h — Pmáx=120Patm — 120.Patm= dágua.g.h — 120.105 = 103.10.h — h=120.105/104 — h=1200m.
R- C
02- Cálculo da altura h da parte imersa com a balsa de massa m=150000kg sem carga — o empuxo E, força vertical e para cima corresponde ao peso do volume de líquido deslocado, no caso, o volume de um paralelepípedo de comprimento 30m, largura 10m e altura h — E=dágua.g.Vimerso — E=103.10. (30.10.h) — E=300.104h.
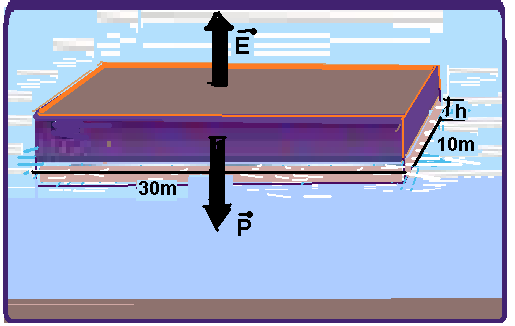
Peso da balsa sem carga — P=mg=150.103.10 — P=150.104N.
Estando a balsa em equilíbrio vertical, flutuando, o peso deve anular o empuxo — P = E — 150.104 = 300.104h — h=150/300 —h=0,5m (altura da balsa imersa com ela descarregada).
Observe atentamente na figura que, quando a carga de peso P’ for colocada, a balsa deve afundar
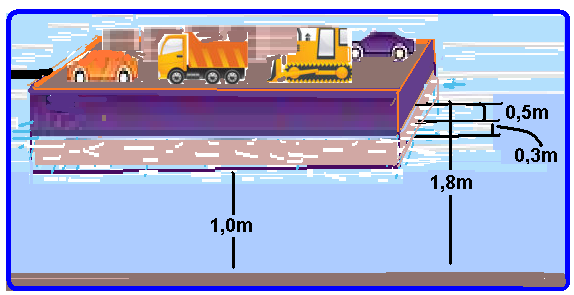
mais 0,3m, pois distância mínima de segurança do fundo do casco para o leito do rio deve ser de 1m.
Assim, o volume de água deslocado por essa carga corresponde ao de um paralelepípedo de comprimento 30m, largura 10m e altura h’=0,3m — V’=30.10.0,3=90m3 e o empuxo produzido será:
E’=dágua.V.g=103.90.10 — E’=90.104N.
Esse empuxo é igual ao peso da carga colocada sobre a balsa P’=90.104N.
R- D
03- O empuxo (força vertical e para cima) é igual ao peso do volume de líquido deslocado e assim, quanto maior o pesomaior será o volume de líquido deslocado e consequentemente, maior será a altura da superfície da água do balde.
Maior peso B (barco + âncora dentro, deslocam maior volume de água) — menor peso A (barco sem
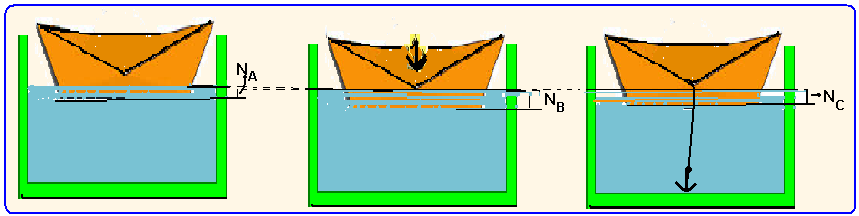
âncora, desloca menor volume de água) — intermediário C (volume deslocado somente pelo barco ) + volume deslocado somente pela âncora).
R- C
04- Bloco C totalmente imerso Vimerso=Vcorpo e em equilíbrio mecânico — Ec = Pc=P — dágua.vimerso.g =P (I).
Bloco A 1/4 imerso e em equilíbrio mecânico — EA= PA — dágua.Vimerso.g = dágua.(1/4)V.g=PA — compare com (I) — P/4 = PA.
Bloco B 3/4 imerso e em equilíbrio mecânico — EA= PA — dágua.Vimerso.g = dágua.(3/4)V.g=PA — compare com (I) — 3P/4 = PA.
R- B.
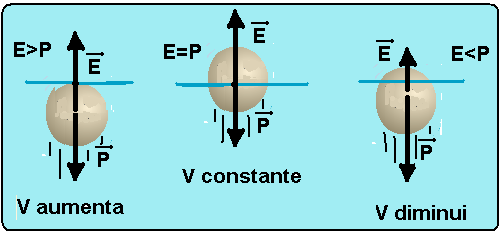
05- I. Correta — veja pelo gráfico que, enquanto totalmente submersa ela sobe com aceleração constante e sujeita a umaforça resultante para cima sendo que, nesse caso, o módulo do empuxo
(força vertical e para cima) deve ser maior que o módulo do peso (força vertical e para baixo).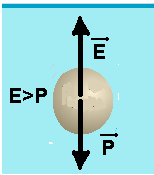
II. Falsa — de 0 a 0,5m a bola está totalmente imersa e o empuxo de intensidade E=dágua.Vbola.g é constante, pois todas as grandezas (dágua.Vbola.g) são constantes.
III. Correta — enquanto totalmente imersa a bola, que partiu do repouso Vo=0 e, após subir h=0,5m atingiu V=7m/s até chegar à superfície, subindo com aceleração de valor — equação de Torricelli — V2 = Vo2 + 2.a.h — 72 = 02 + 2.a.0,5 — a=49m/s2.
Como ela sobe o módulo do empuxo é maior que o módulo do peso — FR=m.a — E – P = m.a —
E – mg = m.a — E – 0,4.10 = 0,4.49 — E= 19,6 + 4 — E=23,6N.
IV. Falsa — veja (II)
V. Correta — a medida que a bola vai saindo da água o empuxo (peso do volume de líquido deslocado) vai diminuindo até que, quando ela está totalmente fora da água, não desloca mais água e o empuxo é nulo.
A respeito das velocidades veja figuras abaixo:
R- C
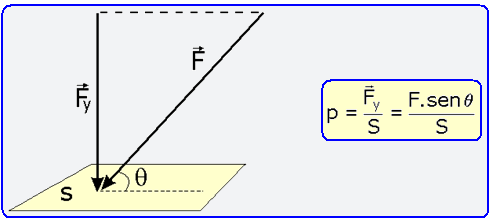
06- Pressão (P) é uma grandeza física obtida pelo quociente entre a intensidade da força (
) e a área (S) em que a força se distribui. Observe na figura abaixo que a força (
) que produz a pressão sobre a área S é perpendicular à mesma.
No caso do exercício a força é a hidrostática, devida à pressão hidrostática e também é
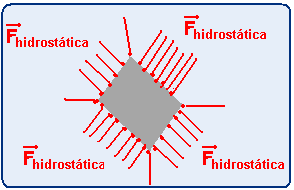
perpendicular à área da superfície em cada ponto.
R- A.
07– Peso de cada corpo — Pc=dc.vcg=mcg — Empuxo de cada corpo — E=dL.Vi.g — como estão flutuando estão em equilíbrio e P = E — mc.g = dL.Vi.g — Vi=mc/dL — como a massa do corpo é a mesma e o líquido é o mesmo (mesma dL) o volume imerso é o mesmo para os três sólidos.
R- D
08- Peso do bloco — P=mg=0,05.10 — P=0,5N.
Força de tensão no fio — fornecida T=89,5N.
Empuxo — E=ρ.V.g=400.0,25.10 — E=1000N.
Na figura abaixo estão colocadas todas as forças que agem sobre o bloco que, como está em
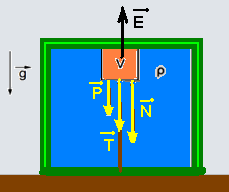
equilíbrio a força resultante sobre ele deve ser nula e, para que isso ocorra — E = P + T + N —
1000 = 89,5 + 0,5 + N — N=910N.
R- C
08- Em cada litro de álcool hidratado têm-se — 0,96L de álcool (96%) e 0,04L de água (4%) — massa de álcool — dálcool=málcool/Válcool — 800g/L=málcool/0,96L — málcool=768g — massa de água — dágua=mágua/Vágua — 1.000g/L=mágua/0,04L — mágua=40g — dmistura=(málcool +mágua)/Vmistura=(768 + 40)/1 — dmistura=808g/L — R- E
09- a) a densidade da esfera leva em conta o volume total — d=m/v=50/30 — d=1,7g/cm3
b) a massa específica leva em conta apenas a parte de volume que contém alumínio — ρ=m/v=/50(30 – 10) — ρ=2,5g/cm3
10- figura 1 — sendo o mesmo volume, o corpo de maior massa terá maior densidade — d4>d1>d3>d2 — figura 2 — d=m/V — como a massa é a mesma para cada bloco, aquele que tiver maior densidade terá menor volume — V4<V1<V3<V2 — 4(A); 1(B); 3(C) e 2(D) — R- C
11- Em cada litro de álcool hidratado têm-se — 0,96L de álcool (96%) e 0,04L de água (4%) — massa de álcool — dálcool=málcool/Válcool — 800g/L=málcool/0,96L — málcool=768g — massa de água — dágua=mágua/Vágua — 1.000g/L=mágua/0,04L — mágua=40g — dmistura=(málcool +mágua)/Vmistura=(768 + 40)/1 — dmistura=808g/L — R- E
12- Quando o corpo estiver na iminência de flutuar, a densidade do corpo é igual à do líquido (mistura) — dmistura=dcorpo=m/V=90/100 — d=0,9g/cm3 — R- A
13- a) O avião decola a partir do instante de t=10 s, pois é a partir deste instante que a força de sustentação supera o peso da aeronave, que é de 3000 N.
b) Pelo gráfico em t = 20s tem-se uma força de sustentação F = 3000 N — essa força atua sobre uma área de S=50m2 — Δp = F/S = 3000/50 — ΔP=60N/m2=60Pa
14- A área de contato é a do cubo inferior — S=10-1.10-1 — S=10-2m2 — P=F/S — 103=F/10-2 — F=10N=peso dos 4 cubos —cada cubo tem p=10/4=2,5N — m=2,5/10 — m=0,25kg — d=m/V =0,25/10-3 — d=250kg/m3
15- Pint = 0,95.105N/m2 — Patm = 1,00.105 N/m2 — A = 0,10 m2 — P = 40 N — na placa agem as seguintes forças — P- peso da placa — F- força devida à diferença entre as pressões externa e interna na câmara — N – força vertical de contato entre as paredes da câmara e a placa — essas forças são mostradas na figura: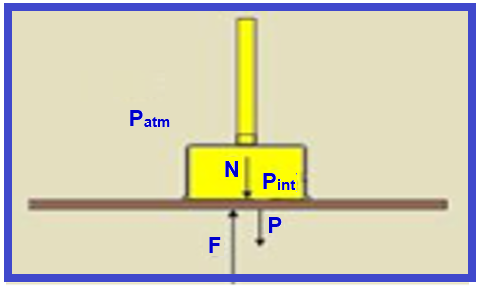
A resultante das forças que agem sobre a placa é nula, pois ela está em equilíbrio — N + P = F — N=F – P=(Patm – Pint).A – P — N=(1,00 – 0,95).105.(0,10) – 40=500 – 40 — N=460N
16- Sendo a densidade da água dágua=1,00g/mL (quando você tem 0% de etanol) — 1,00g – 1mL — mágua g — 50mL — mágua =50g — sendo a densidade do etanol detanol=0,79g/mL(quando você tem 100% de etanol) — 0,79g – 1mL — metanol g — 50mL — metanol =39,5g — massa total de água a 20oC — mtotal= 50g (água) + 39,5g (etanol)=89,5g (água + etanol) — se você observar no gráfico verá que a densidade da mistura que contém 50% de etanol vale dmistura=0,93g/mL — dmistura=mmistura/Vmistura — 0,93 = 89,5/Vmistura — Vmistura≈ 96 mL — R- E
17- A pressão no fundo do recipiente varia linearmente com a altura e independe da área de seção reta de cada cilindro — R- A
18- P1=ρ.g.h — P2=1,2ρ.g.h’ — P1/P2=ρ.g.h/1,2ρ.g.h’ — P1=P2=P — 1= ρ.g.h/1,2ρ.g.h’ — h’=1/1,2h10/12h=5/6h — h – 5/6h=(6h – 5h)/6=h/6 — h’=h/6 — R- B
19- Dados — Z = 100 mL/s = 0,1 L/s — d = 1 kg/L = 103 kg/m3 — Pcol.deágua = 103Pa — g = 10 m/s2 — pelo teorema de Stevin a pressão da coluna líquida é — Pcol.deágua =dgh — 103=103.10.h — h=0,1m — caixa cúbica de volume 1m3 tem área da base Ab=1m2 — cálculo do volume derramado — V=Ab.h=1.(0,1) — V=0,1m3=100L — a vazão (Z) é a razão entre o volume derramado e o tempo — Z=V/Δt=100/0,1 — Δt=103s — R- D
20- Teorema de Stevin — observe a figura abaixo:
Teorema de Stevin — A pressão no ponto B devida apenas à coluna líquida Plíquido=dlíquido.g.h é chamada depressão hidrostática e PB=Patm + dlíquido.g.h é chamada de pressão total, pressão absoluta ou simplesmente pressão.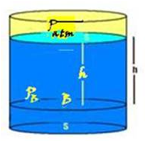
A pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h).
O gráfico da pressão total P em função da altura “profundidade” h, (P=Patm+ d.g.h, que é uma função do primeiro
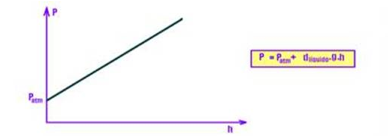
grau)), é uma reta inclinada.
A pressão devido á coluna líquida é maior quanto maior for a profundidade, ou seja, a maior a altura da coluna líquida,
Observe na teoria acima, que a pressão que a água deve exercer para acionar o sifão depende apenas da altura da coluna líquida, não dependendo das dimensões do recipiente, ou seja, do
volume de água nele armazenada — assim, mesmo um pequeno volume de água armazenado, mas com altura suficiente pode acionar o sifão — portanto, a economia deve-se ao volume de água armazenada no tanque — R- B.
21- A alternativa incorreta é a D, pois com a boca da garrafa totalmente tampada a água não jorrará por nenhum dos dois orifícios, pois a pressão externa é maior que a interna — R- D
22-
Observe na figura abaixo que a pressão na superfície da água (ponto Q) é a mesma que aquela devido à altura da coluna de água (ponto p) — PQ=Pp — densidade dágua=103kg/m3 e g=9,8m/s2 — PQ= Patm — Pp==dágua.g.hágua — 1,01.105=103.9,8.hágua — hágua=10,3m — portanto, a pressão atmosférica equilibra uma coluna de água de altura aproximadamente 10m e, essa pressão não consegue empurrar qualquer coluna de água a uma altura superior a 10m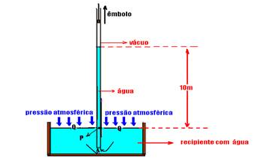
23- a) A pressão do gás no botijão é a mesma que no ponto A (PA=Pgás), que por sua vez é a mesma que no ponto M — Pgás=PM — Pgás=Patm + dHg.g.h=105 + 13,6.103.10.1,04 — Pgás=105 + 14,44.104 — Pgás=1,0.105 + 1,44.105 — Pgás=2,44.105 Pa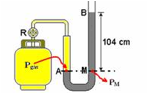
b) Em a — Pgás=F/S — 2,44.105=F/2.104 — F=48,8N
24- a) Na figura II, na extremidade do orifício de altura h1=2,0m a pressão que atua é a pressão atmosférica Po=1,0.105N/m2 — Po=dgh1 + P1 — 1,0.105=1,0.103.10.2,0 + P1 — P1=1,0.105 – 2,0.104 — P1=8,0.104N/m2
b) Chamando de S a área da base do tanque — lei geral dos gases perfeitos — Po.Vo/To=P1.V1/T1 — 1,0.105.S(6,0 – ho)/300 = 8,0.104.S.(6,0 – 2,0)/360 — ho=10/3 m=3,3m
25- Princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal:
“ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido” — R- E
26- Força (F1) ampliada pelo sistema de articulações quando no pedal é aplicada a força F=50N
— colocando o pólo O na articulação central e lembrando que a soma dos momentos das forças em
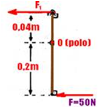
relação ao pólo é nula — – F.d1 + F1.d2=0 — 50.0,2 + F1.0,04=0 — F1=250N — essa força é transmitida até o êmbolo 1 de área S1=40mm2=4.10-5m2 que está ligado, por meio de vaso comunicante até o êmbolo 2 de área S2=80mm2=8.10-5m2 — aplicando o teorema de Pascal
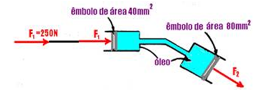
nos êmbolos 1 e 2 — F1/S1=F2/S2 — 250/4.10-5=F2/8.10-5 — F2=500N — R- E
27- Seja F a força aplicada pelo motorista no pedal — pelo enunciado a alavanca tem a
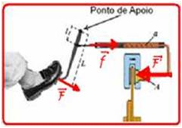
capacidade de ampliação da força aplicada por um fator igual à razão direta de seus braços, que é de 40/10=4 vezes — f=4F — a prensa hidráulica amplia a força f na razão direta de suas áreas, ou seja, de 8 vezes — F’=8f — F’=8.4F — F’=32F — R- A.
28– Sendo o líquido que envolve o recipiente a água e o líquido que o está preenchendo também a água (mesma densidade), para cada unidade preenchida com água, o recipiente desce também uma
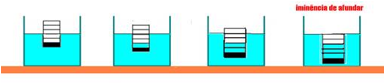
unidade — Observe atentamente a sequência de figuras abaixo e verifique que a resposta é a C
R- C
29- A maioria dos peixes ósseos apresenta bexiga natatória (atualmente denominada vesícula gasosa), uma bolsa cheia de gases acima do estômago cujo volume é regulado por meio de trocas de gases com o sangue e, pela sua dilação ou contração, determina a posição do peixe na água. Para aumentar a profundidade, os peixes contraem a bexiga natatória e, com isso, aumentam a sua densidade tornando-se mais pesado que a água e descendo. Ao subir, fazem o contrário.
R- A
30- Na figura I, No é a indicação da balança — No=P
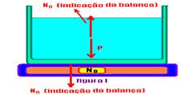
Na figura II, se o corpo imerso recebe do líquido uma força vertical e para cima (Empuxo), pelo princípio da ação e reação o corpo reage sobre o líquido com força de mesma intensidade (Empuxo), mesma direção (vertical) e sentido sentido contrário (para baixo).
A balança indica apenas as forças que agem no líquido, indicadas na figura da direita acima, que são: peso P do sistema (recipiente mais líquido), empuxo sobre o líquido (E) e a reação normal da balança (indicação da balança N) — N=P + E — da figura I — No=P — N=No + E — N – No=E — assim, o empuxo é fornecido pela diferença entre as indicações da balança antes e depois de imergir a esfera.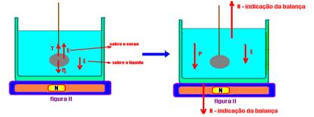
R- (4 + 8)=12
31-
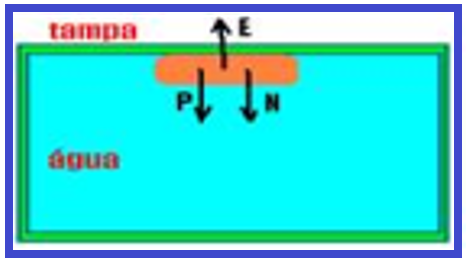
Forças que agem sobre o bloco — peso P (vertical e para baixo) — N força que o bloco troca com a tampa (vertical e para baixo) — empuxo E (vertical e para cima) — P + N=E — mg + N=d.V.g — dbloco.V..g + N=dágua.V.g — N=dágua.V.g – dbloco.V.g — N=(1,0.103 – 0,25.103).V.g — N=0,75.103.V.g — P= 0,25.103.V..g — N/P=(0,75.103.V.g)/(0,25.103.V.g) — N/P=3
32- a) volume de água deslocada — Vimerso=S.H=8.10-3.5.10-2 — Vimerso=4.10-4m3 — estando o recipiente em equilíbrio — P=E — mg=dágua.Vimerso.g — m=1.000.4.10-4 — m=0,4kg
b) nesse caso, o recipiente está na iminência de afundar, e sua massa será mc (massa dos
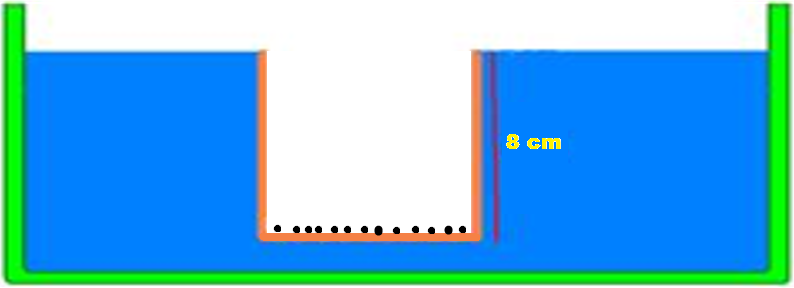
chumbinhos) + m (massa do recipiente) — Vimerso= S.h=8.10-3.8.10-2 — Vimerso=64.10-5m3 — peso do recipiente + peso dos chumbinhos=Ps=(m + mc).g — equilíbrio — Ps=E — (m + mc).g=dágua.Vimerso.g — (0,4 + mc)=1.000.64.10-5 — mc=0,64 – 0,4 — mc=0,24kg=240g — nchumbinhos=240/12 — nchumbinhos=20
c) não mudariam — observe na expressão seguinte que a aceleração da gravidade se cancela — P=E — dcVc.gmarte=dágua.Vágua.gmarte — assim , g não interfere na rwesolução.
33- a) A massa do recipiente, da água e do barquinho sobre a balança é a mesma, quer o barquinho esteja flutuando, quer esteja submerso. Portanto, M1 = M2 .
b) Quando o barquinho está flutuando, o empuxo sobre ele é igual a seu peso e, portanto, maior do que o empuxo quando submerso. Sendo maior o empuxo no barquinho flutuando, o volume da água por ele deslocado nesse caso é maior do que o volume da água por ele deslocado quando está submerso. Uma vez que o volume dentro do recipiente sob o nível da superfície livre da água é o volume da água acrescido do volume de água deslocado, concluímos que o volume dentro do recipiente sob o nível da superfície livre é maior com o barquinho flutuando do que com o barquinho submerso. Assim,a altura da superfície livre com o barquinho flutuando é maior do que a altura da superfície livre com o barquinho submerso, ou seja, h1 > h2 .
34- Veja figuras — a = 4 cm — dágua = 1 g/cm3 — Aimersa = 0,7.Atotal — Δh = 0,50 cm — a área
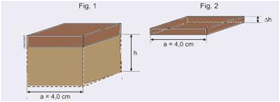
imersa é a área do fundo mais uma parte da área das 4 paredes laterais, de altura h — de acordo com o enunciado — Aimersa=0,7ªtotal — a2 + 4ah=0,7.6.a2 —
4 h = 3,2 a — h = 0,8 a — como o cubo é um sólido reto e está em equilíbrio em água, seu peso é equilibrado pelo empuxo:
P = E — dcubo.Vtotal.g = dágua.Vimerso.g — dcubo/dágua=Vimerso/Vtotal — dcubo/1=a2h/a3 — dcubo=a2.0,8ª/a3 — dcubo=0,80 g/cm3 —
o aumento do empuxo equilibra o peso da rã — Pr=ΔE — mg=dágua.ΔV.g — m=dágua.A.Δh — m=1,0.16.0,5 — m=8,0g —
R- E
35- a) Dados — m=500kg — Vo=20m/s — V=0 — ∆S=20m — cálculo do módulo da aceleração de retardamento do carro aplicando a equação de Torricelli — V2=Vo2 + 2.a.∆S — 02 = 202 + 2.a.20 — a=-400/40= – 10m/s2 em módulo — a=10m/s2 — intensidade da força resultante — FR=ma — Fm=500.10=5000N — cada pistão recebe uma força de F’=5000/4=1250N — como o disco de freio
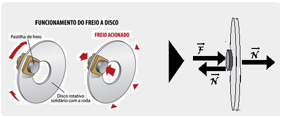
é comprimido pela pastilha nos dois lados pela força pedida de intensidade N (força com que a pastilha pressiona o freio de disco) — F’=2N — 1250=Fat=μ.2N — N=1250/2μ — N=1250/2.08=1250/1,6 — N=781,25N.
b) Área do pistão — S=π.R2=3.(2.10-2)2=12.10-4m2 — P=F/S=781,25/12.10-4 — P=6,5.105Pa.
36- a) Sim; conhecendo a pressão manométrica (o quanto a pressão interna é maior que a externa) e a área de contato com o solo, é possível conhecer a força resultante exercida pela pressão sobre o solo. No equilíbrio e no plano horizontal, essa força é igual em módulo à força de reação que o solo exerce sobre o pneu. Somando-se as forças de reação do solo sobre todos os pneus, encontramos a força de reação total do solo. Na situação de equilíbrio, e no plano horizontal, essa força de reação total do solo é igual em módulo à força peso do automóvel.
b)A área de contato de cada um dos 4 pneus com o solo vale — S=110cm2=110.10-4m2 — força exercida pelos dois pneus dianteiros — um pneu — Pd=Fd/S — 21.104=Fd/110.10-4 — Fd = 2310N — como são dois pneus — Fd=4 620N — força exercida pelos dois pneus traseiros — um pneu — Pd=Fd/S — 22.104=Fd/110.10-4 — Fd = 2 240N — como são dois pneus — Fd=4 480N — a soma dessas 4 forças correspondem ao peso do automóvel — P = 4 620 + 4 480 — P= 9 460N.