Física Térmica – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Física Térmica
01- Quando a temperatura for de T=185oC — 185=160.2-0,8t + 25 — 160=160.2-0,8t — 160/160=2-0,8t — 1=2-0,8t — 20=2-0,8t — 0,8t=0 — t=0 (quando T=185oC, começou a contagem do tempo) — quando a temperatura for de T=65oC — 65=160.2-0,8t + 25 — 40=160.2-0,8t — 40/160=2-0,8t — 1/4=2-0,8t — 2-2=2-0,8t — 0,6t=2 — t=20/8=2,5min — R- C
02- Observe no gráfico que, quando C=0oC, X=25oX e que, quando C=10oC, X=85oX.
Equação de conversão:
Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir, de acordo com a relação matemática baseada no teorema de Thales:
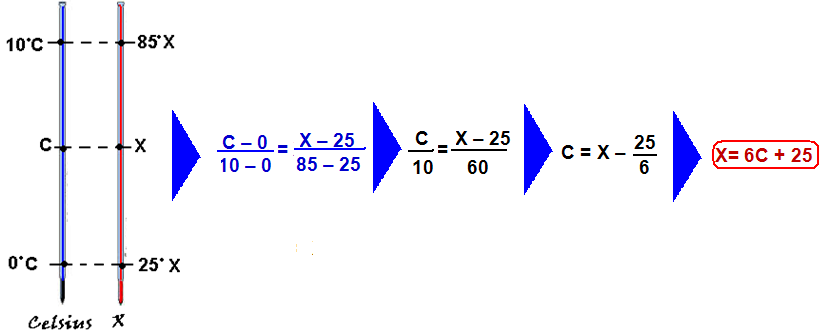
Calor específico (sensível da liga metálica — Cl=0,1cal/(g.oX) — observe que, para cada variação de 10oC (10 – 0) na Celsius,ocorre uma variação de 60oX (85 – 25) na escala X.
Regra de três:
![]()
Portanto cl = 0,1o g/(cal.oX)=0,1 cal/g.(1/6)oC — cl=0,6 cal/goC

Qa + Ql = 0 — 100t – 2000 + 120t – 9000 = 0 — t=11000/220 — t=50oC.
03- I. Correta
Máquina 1 — temperatura da fonte fria em graus kelvin — Tf=227 + 273=500K — temperatura da fonte quente em graus kelvin — Tq=527 + 73=800K — o rendimento η de uma máquina de Carnot, em função da temperatura absoluta é fornecido por η1= 1 – Tf/Tq = 1 – 500/800= 1 – 5/8=3/8 — η1=0,375=37,5% — η1=37,5% Máquina 2 — temperatura da fonte fria em graus kelvin — Tf=227K — temperatura da fonte quente em graus kelvin — Tq=527K — o rendimento η de uma máquina de Carnot, em função da temperatura absoluta é fornecido por η2= 1 – Tf/Tq = 1 – 227/527=0,57 — η2=57% —
portanto η2 > η1
II. Falsa
É fornecido o trabalho realizado pela máquina 1 — W=2000J — rendimento da máquina 1, calculado em I — η1=0,375 — deve-se determinar a quantidade de calor Qq que a máquina recebe da fonte quente — a expressão que relaciona essas grandezas é — η1=W/Qq — 0,375=2000/Qq — Qq=2000/0,375≈5333,3J — esse valor é diferente de 6000J.
III. Correta
É fornecido que a máquina 2 retirou 4000J da fonte quente — Qq=4000J — rendimento da máquina 2 calculado em I — η2=0,57 — η2=W/Qq — 0,57=W/4000 — W=2280J — utilizando a relação a seguir — Qq= W + Qf — 4000=2280 + Qf —Qf=1720J.
IV. Falsa
Observe na expressão η = 1 – Qf/Qq que, para uma mesma quantidade de calor retirada da fonte quente, ou seja, para um mesmo Qq, o rendimento η e a quantidade de calor rejeitada para a fonte fria Qf são inversamente proporcionais — sendo η2> η1, Qf2 será menor que Qf1.
R- B.
04- Pelo enunciado, durante o processo de varredura ocorre a formação de uma película de água líquida entre a pedra e a pista, ou seja, está havendo uma fusão, uma passagem do estado sólido para o líquido.
Assim, a transformação promovida pela varredura é a de número 1.
05- Dados — Lo=5m — α=10-5 oC-1 — to=20oC — no dia mais quente do verão t=40oC o bloco se dilatará de ΔL=Lo.α.(t – to)=5.10-5.(40 – 20)=100.10-5=10-3m — ΔL=10-3.102=0,1cm — para que no dia mais quente do verão a distância deva ser de 1,0cm você deve resguardar, prever, uma distância de 1,0 + 0,1=1,1cm.
R- B
06-Se uma placa metálica com orifício for aquecida, verifica-se que o orifício aumenta, como se

fosse constituído pelo material da placa, pois tudo se passa como se o furo tivesse um coeficiente de dilatação superficial igual àquele da substância da placa.
Como o diâmetro interno é metade do externo, se o externo se dilata de Δd, o interno se dilatará de Δd/2.
R- D
07- ΔL=Lo.α.(t – to)=50.1,2.10-5.(45 – 5)=2400.10-5=0,024m=2,4cm (dilatação do trilho) — o novo espaçamento será — d=4,4 – 2,4=2,0cm.
R- E
08- Para cada (14 – 2)=12cm a temperatura sobe de (46 – 34)=12oC, donde você conclui que para cada 1 cm corresponde uma variação de 1oC.
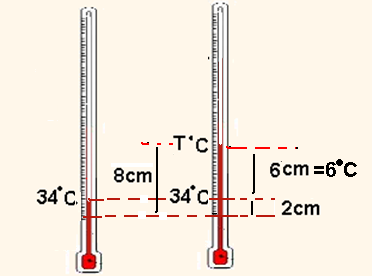
Observe na figura acima que, quando a temperatura passou de 34oC para T, a coluna de mercúrio sofreu uma elevação de 6cm=6oC e, assim, a temperatura T será de T=34 + 6=40oC.
R- D
09- Você vai misturar V água fervida (100oC) com (15L- V) de água a 20oC para obter água a 27oC — V.c.(27 – 100) + (15 – V).c.(27 – 20) = 0 — – 73V + 105 – 7V = 0 — V=1,3L.
Regra de três — 15L – 100% — 1,3L – P — P=130/15=8,7%.
R- D
10- Observe na figura abaixo que Δθ=30ºC=π/6 rad e que Δθ=ΔL/R — π/6 = ΔL/0,3 — ΔL=0,3π/6=
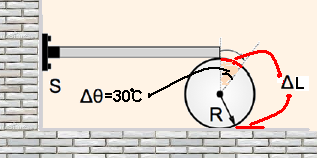
0,1π/2 — ΔL=0,05π — ΔL=5.10-2π m.
Da equação fundamental da calorimetria — ΔL=Lo.α.ΔT — 5.10-2π = 2.5π.10-4.ΔT — ΔT = 5.10-2 =
10-3 — ΔT = 50K.
ΔT = T – To — 50 = T – 298 — T= 348K – 273=75oC.
R- B
11- Uma dada porção de ar ocupa um volume V numa determinada temperatura T — o exercício fornece — pressão parcial do vapor de água — Pvapor=3.103Pa — pressão do ar (pressão atmosférica — Patm=1.105Pa — sendo os gases ideais você pode aplicar — P.V=n.R.T — sendo — P (pressão); V (volume); n (quantidade de moléculas); R (constante) e T (temperatura absoluta) — para o vapor de água — Pv.V=nv.R.T — 3.103.V = nv.R.T (I) — para o ar atmosférico — Par.V=nar.R.T — 1.105.V=nar.T (II) — (I)/(II) — 3,103V/1.105=nV.R.T/nar.R.T — 3.103/1.105=
nV/nar — é pedido nv/nar=3.103/1.105 — porcentagem= nv/nar=3.10-2=0,03×100 — porcentagem=3% — R D.
12- Se você não domina a teoria, ela está detalhada a seguir:
Princípio das trocas de calor
![]() Colocando vários corpos a diferentes temperaturas no interior de um recipiente adiabático, haverá trocas de calor entre eles, até atingirem o equilíbrio térmico. Assim , como o recipiente é adiabático, a quantidade de calor cedida pelos corpos mais quentes é igual à quantidade de calor recebida pelos mais frios: Princípio da Conservação da energia.
Colocando vários corpos a diferentes temperaturas no interior de um recipiente adiabático, haverá trocas de calor entre eles, até atingirem o equilíbrio térmico. Assim , como o recipiente é adiabático, a quantidade de calor cedida pelos corpos mais quentes é igual à quantidade de calor recebida pelos mais frios: Princípio da Conservação da energia.
Como a quantidade de calor recebida é positiva e a recebida é negativa, tem-se que — Q1 + Q2 + Q3 + ….+ QN = 0 ou
M1.c1.(t – t01) + m2.c2.(t – t02) + m3.c3.(t – to3) + … + mN.cN.(t – t0N) = 0
![]() Calorímetros – são recipientes adiabáticos onde se estuda as trocas de calor entre corpos que
Calorímetros – são recipientes adiabáticos onde se estuda as trocas de calor entre corpos que

são colocados em seu interior. Normalmente utiliza-se o calorímetro para se medir o calor específico de um corpo de massa (mc), mergulhando-o no interior do calorímetro, onde se tem água de massa (ma), um termômetro e um agitador de líquido. Aquece-se o corpo cujo calor específico você deseja determinar e o introduz na água do calorímetro. Agita-se o sistema, espera ser atingido o equilíbrio térmico (te) que é medida. Conhecendo as temperaturas iniciais da água e do corpo e o calor específico da água, determina-se o calor específico (cc) do corpo pela expressão — mc.cc.(te – toc) + ma.ca.(te – toa) = 0.
No caso do exercício, observe que o calorímetro e a massa de 100g de água a 2oC que já estavam em seu interior não vão influir nas trocas de calor já que as temperaturas inicial e final são iguais (20oC) — assim, os 200g de água a 100oC devem passar para a água a 20oC quando misturados com uma massa m de água a 0oC, que também deve passar para 20oC — Qcedido + Qrecebido=0 — 200.1.(20 – 100) + m.1.(20 – 0) = 0 — 16000 = 20m — m=800g — R- B.
13- Nos próximos 50 anos (5 décadas) de acordo com os mareógrafos o aumento do nível global dos mares e oceanos será de 5.(1,7cm)=8,5cm — nos próximos 50 anos (5 décadas) de acordo com os altímetros-radares o aumento do nível global dos mares e oceanos será de 5.(3,1cm)=15,5cm — então, o nível das águas dos mares e oceanos deverá subir entre 8,5cm e 15,5cm — R- A.
14- Em Santos, ao nível do mar, a pressão atmosférica é maior do que em La Paz (maior altitude), onde também é maior a concentração de O2por volume de ar inspirado — para compensar esses dois fatores, os atletas que moram em locais de altitude elevada (por exemplo, La Paz) acabam apresentando uma maior quantidade de hemácias no sangue, o que justifica um melhor desempenho deles, quando o jogo ocorre em locais mais altos — porém, ao nível do mar, a quantidade de hemácias presente no sangue do atleta que mora nessas regiões é suficiente para levar, aos tecidos, o O2 necessário para a atividade física.
R- E.
15- Numa situação você esta movimentando o ar externo (menos ar, que é expelido com maior pressão) na outra o ar vem do interior do seu sistema respiratório, portanto mais aquecido (mais ar, expelido com menor pressão) — R- E.
16- Trata-se apenas de uma mudança de estado (fusão a 0oC) — Q=m.LF=3.10.80=2400=2,4.103cal — R- E.
17- Trata-se do Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia que afirma que: “A energia não pode ser criada nem destruída, mas apenas transformada”
Suponha que um sistema isolado receba 300J de calor. Se, por exemplo, 50J dessa energia forem absorvidos pelo sistema, então a parte restante, 250J, será fornecida ao ambiente sob a forma de trabalho.

Então, Q= W + ΔU ou,
![]()
A expressão acima é a representação matemática do primeiro princípio da termodinâmica.
R- C.
18- A) Q=m.c.(θ – θo)=10.1.(100 – 25)=750kcal.
B) lenha — regra de três — 1kg – 2500kcal — 3kg – QL — QL=2500×3=7500kcal — GLP — regra de três — 1kg – 12000kcal — 0,125kg – Q’ — Q’=0,125×12000=1500kcal
C) EL=750/7500=0,1=10% — EGLP=750/1500=,5=50%.
19- Expressão da dilatação linear — ∆L=Loα∆θ — ∆L/∆θ=Loα — sendo as duas retas paralelas a tangente do ângulo θ entre as duas é a mesma — tgθ=∆LB/∆θ=∆LA/∆θ — ∆LB = ∆LA — LoB.αB = LoB.αB — 2LαB = LαA — αA/αB=2.
R- A.
20- a) Falsa — C/5 = (F – 32)/9 — quando eles indicarem valores iguais C=F=x — x/5 = (x – 32)/9 —5x – 160 = 9x — x=F=C= -40oC (quando a Celsius indicar – 40oC a Fahrenheit indicará também – 40oF).
b) Falsa — veja (a).
c) Correta — ∆C/5 = ∆F/9 — 5∆F=9∆C — ∆F=1,8∆C — a uma variação de 1o na escala Celsius corresponde uma variação de 1,8o na escala Fahrenheit.
d) Falsa — a altura da coluna líquida é a mesma para os dois termômetros, pois se trata do mesmo líquido e, portanto, para a mesma variação de temperatura sofrem a mesma dilatação volumétrica.
R- C.
21- Leia abaixo o processo de transferência de calor por condução:
Condução térmica
O calor é conduzido de um ponto a outro do corpo sem que haja deslocamento das partículas.

Explicando microscopicamente o fenômeno: a região próxima da chama tem o movimento vibratório de suas moléculas aumentado, adquirindo assim maior energia cinética, que é transferida através de choques às partículas vizinhas, que também aumentam seu movimento vibratório. Através desse transporte de energia, toda a barra é aquecida, pois os
metais são bons condutores de calor — maneira que este tipo de cooler refrigera o processador segue um princípio bem simples: o calor gerado pelo processador é transferido devido à diferença de temperaturas entre eles, para o metal do cooler por condução, que ao mesmo tempo é resfriado pela corrente de ar trazida pela ventoinha, provocando nova transfência de calor do processador para o cooler e assim sucessivamente — vale ressaltar que a condução de calor do processador para o metal é potencializada por uma pasta térmica especial para este tipo de situação.
R- C.
22- Pelos dados você pode observar que no final haverá água líquida à temperatura t — calor cedido por m=10g de gelo a -10oC até água a t — Q1=m.cgelo.(t – to) + m.L + m.cágua.(t – to)=10.0,5.{0 – (-10)} + 10.80 + 10.1.(t -0) — Q1=10t + 850 — calor cedido por 90g de água para a 50oC até chegar a água a t — Q2=mcágua.(t – to)=90.1.(t – 50) — Q2=90t – 4500 — Q1 + Q2=0 — 10t + 850 + 90t – 4500 = 0 — 100t=3650 — t=36,50oC — R-C.
23- Cilindro na vertical — volume inicial Vo=3L=3.10-3m3 — área de seção transversal S=20cm2=20.10-4m2=2.10-3m2 — pressão=força (no caso o peso do êmbolo)/área —Pr=P/S=52/2.10-3
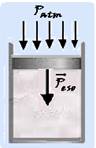
— Pr=26.103N/m2 — com o cilindro na vertical a pressão total sobre o gás será — Pt=Pr + Patm=26.103 + 1.103 — Pt=27.103N/m2 — cálculo do volume final V — pelo enunciado trata-se de uma transformação isobárica (pressão constante) — Po.Vo/To = P.V/T —
Vo/To = V/T — 3.10-3/573 = V/673 — V=673×3.10-3/573 — V=2019.10-3/573 — V=3,52.10-3m3 — o trabalho realizado pelo gás ideal numa transformação isobárica é dado por Wv=Pt.∆V=27.103(3,52.10-3 – 3,00.10-3)= 27.103x 0,52.10-3 — Wv=14,04J — cilindro na horizontal — agora não tem mais o peso do êmbolo e a pressão exercida no

êmbolo é a atmosférica — Patm=1.103N/m2 — sendo a transformação isobárica, a variação de volume ∆V é a mesma que a do cilindro na vertical — ∆V=0,52.10-3m3 — Wh=Patm.∆V=1.103x0,52.10-3 — Wh=0,52J — é pedido ∆W = Wv – Wh=14,04 – 0,52 — ∆W=13,52J — R- C.
24- a) Trata-se do calor específico (sensível), pois a temperatura está aumentando o que significa que não ocorreu mudança de estado.
b) Substância B — enquanto a temperatura variou de 20oC a 30oC, a substância B recebeu QB=2.103cal — equação fundamental da calorimetria — QB=m.cB.∆T — QB=m.cB.(T – To) — 2.103=400.cB.(30 – 20) — cB=2.103/4.103 — cB=0,5 cal/goC.
Substância A — enquanto a temperatura variou de 20oC a 25oC, a substância A recebeu QA=2.103cal — equação fundamental da calorimetria — QA=m.cA.∆T — QA=m.cA.(T – To) — 2.103=400.cA.(25 – 20) — cA=2.103/2.103 — CA=1,0 cal/goC.
A substância A possui maior calor específico
c) Potência=energia/tempo — Po=W/T — 400cal/min=W/30 — W=12000cal — W=12.103cal — W=Q=12kcal — Q=m.cA.∆T — 12.103=400.1.(T – 20) — T=50oC — se a enzima chegar a valores muito elevados de temperatura que variam para cada organismo, em média 45°C a 50°C, as enzimas sofrerão um desenrolamento de sua estrutura, perdendo suas propriedades biológicas — esse processo é chamado de desnaturação enzimática.
