Reflexão da Luz e Espelhos Planos – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Reflexão da Luz e Espelhos Planos
01- Traçando a normal N e prolongando o raio incidente, obtemos os ângulos de incidência i e de reflexão r e também o desvio d
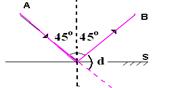
d=180 – 90 — d=90o R- B
02- R- 60o – veja figura abaixo
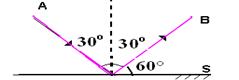
03- Não, também é verdadeira para os espelhos curvos.
04- R- D – Veja esboço abaixo
05- Localizar O’, imagem de O. Unir O’ à P. O raio de luz deve partir de P, atingir o espelho em D, sofrer reflexão e atingir o olho do
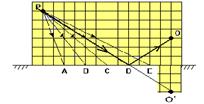
observador O. R- B
06- a) Determinando a região do campo visual do espelho, verificamos que somente o ponto P se encontra nela.

b) Sim, somente o ponto P.
07- R- 40 cm – (veja teoria)
08- R- 60o – (veja teoria)
09- O caminhão X se aproxima do carro com velocidade relativa de VXo=50 – 40 =10km/h e a jovem vê, pelo espelho retrovisor, sua imagem se aproximar com o dobro desse valor, ou seja, VXi=20km/h.

Então o caminhão Y, para manter velocidade relativa de 10km/h deve se mover para a direita com velocidade de VYo=30 – 20=10kmh R- E
10- Observe na figura abaixo a região de campo visual do espelho. Para entrar nela, o amigo percorreu 3m, com velocidade constante
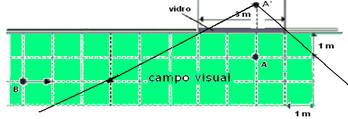
de 1m/s — V=ΔS/ Δt — 1=3/ Δt — Δt=3s R – B
11- A imagem da bola está atrás do espelho (em P’) e a 2unidades (2u), do espelho.
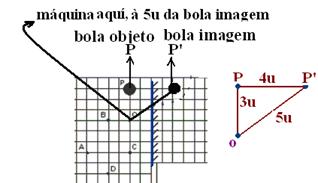
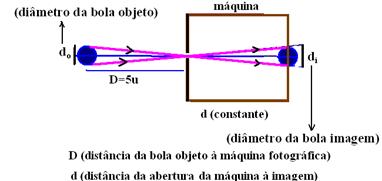
Observe nas figuras acima que d e do são constantes e que se, numa máquina fotográfica quisermos diminuir di à metade devemos
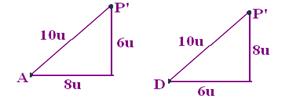
duplicar D, que deve passar a ter 10u. A alternativa que satisfaz à essa condição é a E.
12- Prolongar o espelho para a esquerda. Localizar a imagem (A’) de Joãozinho atrás do espelho. Traçar um feixe luminoso que saia
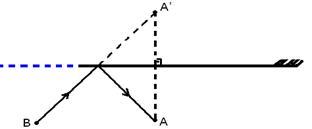
de Maria, incida no espelho e atinja Joãozinho.
13- R – E (veja teoria)
14- R- D (veja esquema abaixo)
15- Observe no esquema abaixo que:
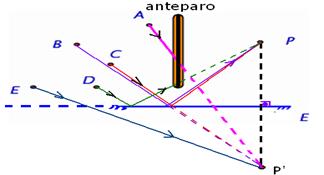
O raio incidente A é interrompido no anteparo e não é visto. Os raios B e C incidem no espelho e se refletem atingindo os olhos do observador P, que os vê. O raio refletido D é interrompido no anteparo não atingindo os olhos do observador que não o vê. O raio E não atinge o espelho não sofrendo, portanto, reflexão e não atingindo o observador. R- D
16- Se o espelho se deslocou de d=50 – 30=20cm, a imagem do objeto se deslocará de d’=2.20=40cm (veja teoria)
17- R- E
18- Como o ângulo de reflexão possui a mesma medida do ângulo de incidência as distâncias da mosca ao espelho e da mosca à normal serão proporcionais às respectivas distâncias da fonte.
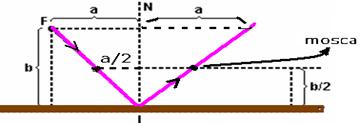
Como a distância da mosca ao espelho é metade da distância da fonte ao espelho, a distância da mosca à normal será a metade da distância da fonte a mesma normal, ou seja, a/2.
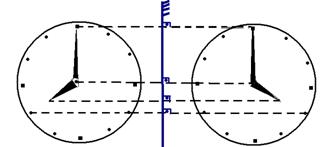
19- Comporta-se como se tivesse um espelho sob a palavra R- B
20- R- B (veja teoria)
21- Traçando dois raios de luz que tangenciam as extremidades do espelho, a região visível atinge
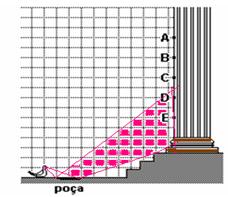
apenas os pontos D e E R- E
22- Localizar, atrás do espelho a imagem (A’) do extremo superior da pessoa (A) e a imagem (B’) do extremo inferior da pessoa (B).
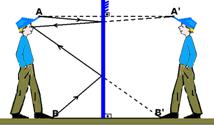
Ligar, com linha pontilhada, A’ e B’ ao olho da pessoa objeto, que interceptam o espelho nos pontos M (inferior) e N (superior),
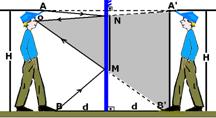
que delimitam o tamanho mínimo do espelho para que a pessoa possa ver-se de corpo inteiro no espelho. Observe que os triângulos oMN e oB’A’ são semelhantes e dessa semelhança tiramos o tamanho mínimo do espelho MN — H/MN = 2d/d —
MN=H/2 – o tamanho mínimo do espelho para que a pessoa se veja de corpo inteiro deve ter a metade da altura da pessoa. R- B
23- I – falsa – a imagem é virtual — e II – falsa é o espelho que gira, mas o raio de luz incide sempre na mesma posição — III- Falsa – (veja resolução anterior) R- E
24- A imagem da pessoa encontra-se sempre ajustada ao tamanho do espelho independente da distância a que ela se encontra do mesmo, mas, à medida que a pessoa se afasta do espelho, sua imagem também se afasta dando a impressão, devido ao ângulo visual, que ela parece menor, mas continua sempre ajustada ao tamanho do espelho. R- C
25- R – B
26- R- C – (veja resolução da questão 24)
27- Localizar s’, imagem de s, e uni-la ao olho da pessoa (figura abaixo).

R- B
28- R- C (veja figura abaixo)
29- Se os raios refletidos giram de 30o, o espelho gira da metade, ou seja, de 15o
30- R – D (veja figura abaixo)
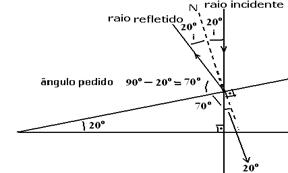
31- R- A
32- R- D (veja esquema abaixo
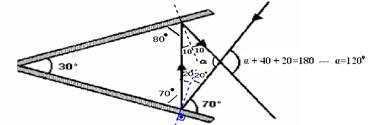
33- R- D (observe a figura abaixo)
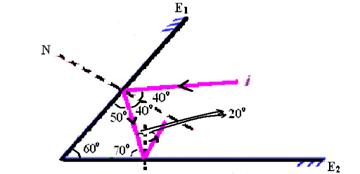
34- É o mesmo que ocorre numa rotação de um espelho plano de 50o onde os raios refletidos giram o dobro, ou seja, β=2.50=100o.
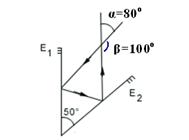
Assim, o ângulo α será α=180 – 100=80o R- E
35- Como o ângulo de rotação do espelho é metade do ângulo de rotação do raio refletido, temos 30/2=15o R- C
36- Determinando o campo visual da região observada pelo gerente que está no ponto C (figura abaixo).
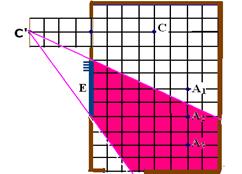
R – D
37- Como o raio de luz refletido por E incide perpendicularmente em E’, ele retorna sobre si mesmo (incidência normal) e pelo
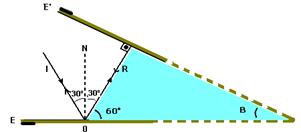
princípio da reversibilidade dos raios de luz, retorna seguindo o mesmo caminho. No triângulo hachurado tem-se — 90o + 60o + B=180o — B=30o R- B
38- Veja a figura abaixo onde se pede para determinar a distância d
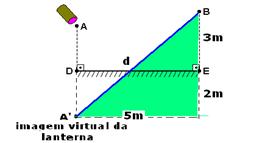
Pitágoras no triângulo hachurado — d2 = 52 + 52=2.52 — d=5√2 m
39- Observe no esquema abaixo onde o espelho foi girado de 60o no sentido horário — sen30o=d/6 — 0,5=d/6 — d=3,0cm —
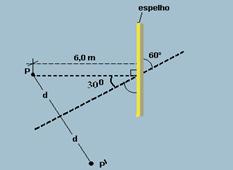
Em relação à posição inicial onde a imagem era P, a nova posição da imagem P’ dista de P — PP’=2d=6,0 cm
40- Observe a figura abaixo — i = r = 60°.
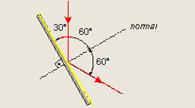
R- E
41- No espelho plano, objeto e imagem são sempre simétricos em relação ao plano do espelho. O ponto simétrico de O é o ponto I.
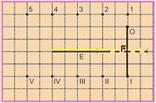
R- A
42- Um dos processos — você localiza a imagem de O que está em I — a partir de I você traça duas linhas que tangenciem as extremidades do espelho — entre essas duas linhas localizadas na frente do espelho está o campo visual — observe a figura —
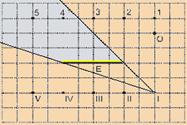
que mostra o campo de visão para a imagem do objeto — nela você pode notar que apenas os observadores colocados nas posições 4 e 5 estão nessa região — R- D
43- Observe na figura as posições do estudante, da árvore e do espelho — os triângulos sombreados são semelhantes — 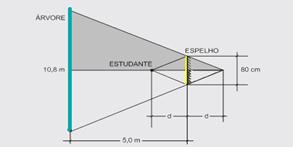
d/0,4=(5 + d)/5,4 — 5,4d=2 + 0,4d — d=0,4m=40cm — R- A
44- Observe o esquema abaixo — 2a + 2b + β=180o=π — (π/2 – a) + (π/2 – b) + θ =π — β = π – 2(a 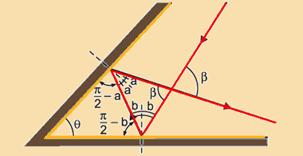
+ b) — θ = a + b — β=π – 2θ — observe que para que o raio incidente seja paralelo ao raio emergente o ângulo β deve ser nulo — β = π – 2θ —
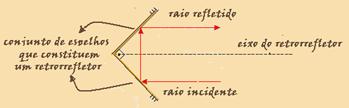
0 = π – 2θ — θ=π/2 — portanto, se θ=π/2 os raios incidente e emergente são paralelos
45- Observe o esquema abaixo — sendo a abertura angular (olho) muito pequena você pode supor a seguinte aproximação —
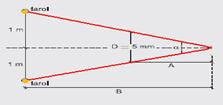
tg(α/2)≈α/2≈1/B — 1/B≈1,22γ/2D — B=2D/1,22γ — B=(2.5.10-3)/(1,22.570.10-9) — B=1,4.104m — sendo a distância B (dos faróis até a abertura do olho=14.000m) muito maior que o comprimento A do olho (aproximadamente 24mm “distância da pupila à retina”), das alternativas apresentadas a mais próxima é a alternativa B — R- B
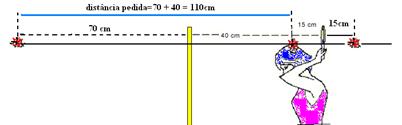
46- A partir dos comprimentos indicados, pode-se desenhar um triângulo retângulo em que a hipotenusa é a distância da moeda de 50
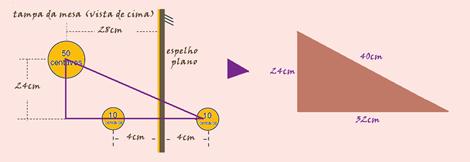
centavos à imagem da moeda de 10 centavos e os catetos valem 24 cm e (28 cm + 4 cm)= 32 cm, onde o segmento de tamanho 4 cm se originou da distância da imagem da moeda de 10 centavos ao espelho — teorema de Pitágoras, a hipotenusa desse triângulo retângulo é igual a 40 cm.
R- D
47- Observe na figura as construções nos dois casos pedidos que foram baseadas na segunda lei da reflexão: os ângulos de incidência e de reflexão são congruentes — no 1º caso a incidência é normal, portanto o ângulo de incidência é α’1 = 0° — no 2º caso,
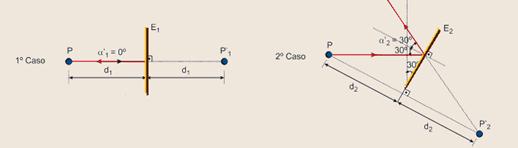
α’2 = 30° — propriedade da simetria — no espelho plano objeto e imagem são sempre simétricos em relação ao plano do espelho — assim, as distâncias objeto-espelho e espelho-imagem são iguais e que o segmento de reta que liga o objeto e a respectiva imagem é perpendicular ao plano do espelho.
48- Na primeira situação, como o vagão está em movimento retilíneo uniforme ele está em equilíbrio dinâmico (mesma situação
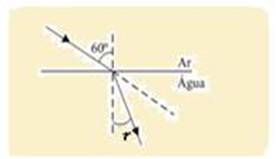
como se estivesse em repouso) — aplicando a lei de Snell — nar.seni=nágua.senr — nar.sen60o=nágua.senr (I) — 1.√3/2=nágua.senr — senr=√3/2nágua (I) — na segunda incidência, com o vagão se movendo para a esquerda com aceleração a=(√3/3)g, a superfície da água se inclinará conforme figura e a normal N formará um ângulo α com a vertical — a intensidade da força resultante é na direção e sentido do deslocamento (movimento acelerado), ou seja, Fr=ma=m.√3/3)g=√3/3)mg — como
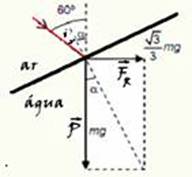
o peso (P=mg) é sempre vertical ele formará um ângulo de 60o com o raio incidente — observe na figura, no triângulo hachurado que tgα=(√3/3)mg/mg — tgα=√3/3 — α=300 — observe ainda na figura que se α=30o, o ângulo de incidência i também será de 30o — i=30o — aplicando novamente a lei de Snell — nar.sen30oi=nágua.senr’ — 1.1/2=nágua.senr’ — senr’=(1/2nágua) (II) — dividindo, como pedido (I) por (II) — senr/senr’=(√3/2nágua)x(2nágua/1) — senr/senr’=√3 — R- D
49- Você deve prolongar o espelho plano e localizar a imagem dos olhos do motorista, atrás do
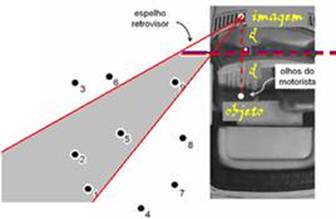
espelho e simétrica ao objeto em relação ao espelho — em seguida, a partir da imagem dos olhos traçar duas retas que tangenciem as extremidades do espelho — a região em frente ao espelho entre essas duas retas é o campo visual do espelho — R- C
50-

a) Chamando de B’ a imagem da ponta dos pés, você deve ligar, com linha pontilhada, B’ ao olho o do rapaz objeto, que intercepta o
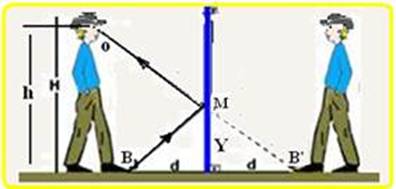
espelho no ponto M — em seguida traçar, a partir do olho do rapaz raios (linhas cheias) de luz que unam oM e MB — para que o rapaz enxergue a imagem da ponta de seu pé, raios de luz devem sair de B, atingir o espelho no ponto M onde sofrem reflexão e atingirem o olho em O.
b) A partir das imagens do topo do chapéu A’ e da ponta dos pés B’ você deve traçar duas linhas pontilhadas que atinjam o olho O do
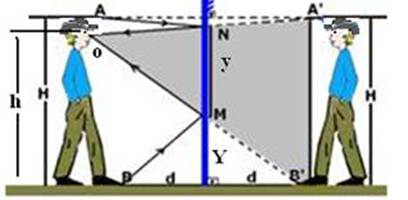
rapaz objeto, que interceptam o espelho nos pontos M (inferior) e N (superior), que delimitam o tamanho mínimo do espelho para que a pessoa possa ver-se de corpo inteiro no espelho. Observe que os triângulos OMN e OB’A’ são semelhantes e dessa semelhança tiramos o tamanho mínimo do espelho MN — H/MN = 2d/d — MN=H/2 — H=2MN=2y — H=2.1=2m — a altura do rapaz deve ter o dobro da altura mínima do espelho para que ele se veja de corpo inteiro no mesmo.
c) Observe na figura abaixo que os triângulos OBB’ e MQB’ são semelhantes — 2d/h=d/Y — 2Y=h — Y=h/2=1,6/2=0,8m
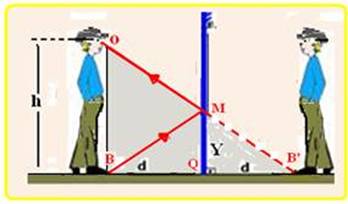
d) Verifique que as expressões obtidas em (b) e (c) são independentes da distância d do rapaz objeto ao espelho — assim, a altura mínima do espelho é sempre a mesma independente do fato de a pessoa estar a uma distância d, 2d, 3d, etc. do espelho. Assim, a imagem da pessoa encontra-se ajustada ao tamanho do espelho independente da distância a que ela se encontra do mesmo, mas, à medida que a pessoa se afasta do espelho, sua imagem também se afasta dando a impressão, devido ao ângulo visual, que ela parece menor, mas continua sempre ajustada ao tamanho do espelho.
