Resolução comentada dos exercícios de vestibulares sobre
Prismas ópticos
01- Veja figura abaixo:
R- B
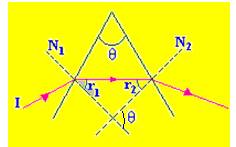
02- Observe a figura abaixo:
d=i + r’ – A — d=50 + 30 -60 — d=20o R- A
03- Se o raio emergir rasante, teremos que o ângulo de incidência i’ na segunda face é igual ao
ângulo limite L que é igual ao ângulo de refringência A, fornecido pela expressão – senL=nmenor/nmaior ® senL=nar/n ®senL=1/n
Como i’=L ® sen i’=sen L ® sen i’=senA=1/n — senA=1/√2 — senA=√2/2 — A=45o R- D.
04- A=60o — i=45o — i’=30o — A=r + i’ — 60=r + 30o — r=30o — Aplicando Snell-Descartes na face onde o raio incide — nar.seni=nv.senr — 1.sen45o=nv.sen30o — 1.√2/2=nv.1/2 — nv=√2
05- Veja a figura abaixo:
Como o raio de luz incide perpendicularmente na primeira fase, ele não sofre desvio até atingir a segunda face quando emerge rasante, onde, aplicando Snell-Descartes — nv.sen60o=nar.sen90o — nv.1,73/2=1.1 — nv=1,15 — R- B
06- I- Como ele incide normalmente no líquido ele não sofre desvio até atingir a interface líquido-
prisma com ângulo de 45o (sen45o=√2/2=0,7) e, nessa interface — cálculo do ângulo limite — senL=nmenor/nmaior=√2/√3=0,8 — como seni<senL — i<L — assim, não haverá reflexão total e sim, refração, penetrando no prisma — Falsa
II- Aplicando Snell-Descartes na interface líquido-prisma — n’.sen45o=n.senr — √3. √2/2=√2.senr — senr=√3/2 — r=60o — Falsa
III – Cálculo de i’ — A=r + i’ — 90=60 + i’ — i’=30o — Aplicando Snell-Descartes na face em que o raio emerge para o ar
— n.sen30o=nar.senr’ — √2. 1/2=1.senr’ — senr’=√2/2 — r’=45o — Verdadeira
IV- Verdadeira — veja que os raios incidente e emergente possuem o mesmo ângulo (45o), portanto possuem direções paralelas.
R- D
07- Visualizando a figura de frente:
Observe que na face AB e CD ele não sofre desvio, pois incide e emerge perpendicularmente e nas outras duas faces sofre reflexão total, pois incide com 45o, que é superior ao ângulo limite que é 42o. R- D
08- Observe na sequência de figuras abaixo que à medida que i diminui no sentido anti-horário, r
também diminui, mas no sentido horário R- E
09- R- A – veja figura abaixo
10- Veja a figura abaixo:
nar.sen60o=nP.sen30o — 1.√3/2=nP.1/2 — nP=√3=1,7
11- Como o raio incide perpendicularmente na face A ele não sofre desvio até atingir a face B, onde incide com ângulo i=45o e sen45o= sen45o = √2/2 = 070 — o ângulo limite na interface prisma-água vale senL=nmenor/nmaior — senL=1,33/1,52 — senL=8,87 — sen45o<senL — 45o<L — incide na face B com ângulo inferior ao ângulo limite, ou seja, não sofre reflexão total em B, mas sim refração, passando para a água. R- A
12- Quando o raio de luz se refrata paralelo à base o desvio (d) tem valor mínimo e o ângulo de incidência é igual ao ângulo de emergência, ou seja, i = r’. Mas, se isso ocorre ® i’ = r e i=r, veja figura abaixo.
A=2r — aplicando Snell-Descartes na primeira face — nar.seni=nv.senr — 1.√2/2=√2.senr — senr=1/2 — r=30o — A=2r=2.30 — A=60o — dmin=d=i + r’ – A=2i – A d=2.45 – 60 — d=90 – 60o — d=30o
13- As trajetórias dos raios incidente, no interior do prisma e emergente se deslocam como se você estivesse girando um “saca-rolhas” no sentido horário, ou seja, o raio incidente sobe, e os outros dois descem conforme as figuras abaixo.
R- A
14- Refração no pontoA — nar.sen60o=nv.senr — 1.√3/2=nv.sen30o — 1.√3/2=nv.1/2 — nv=√3 — incide no ponto B onde sofre refração, pois sen30o=1/2 e senL=nmenor/nmaior=1/√3= √3/3 — assim, como seni<senL — i<L — ele não sofre reflexão total —
Aplicando Snell-Descartes no ponto B — nv.sen30o=nar.senr — √3.1/2=1.senr — senr=√3/2 — r=60o — R- A
15- Observe na figura abaixo que os dois raios de luz incidem com ângulo de 45o — o ângulo limite para o raio azul (a) é de 44oe, como ele incide com 45o que é superior ao ângulo limite, ele sofre reflexão total, retornando ao prisma. O raio vermelho (v) incide também com 45o, que é inferior ao seu ângulo limite (46o), sofrendo refração e passando para o ar. R- E
16- Veja a figura abaixo:
R- D
17- a)
Pelo princípio da reversibilidade dos raios de luz, o caminho na “ida” é o mesmo que na “volta”
b) No ponto A — nv.sen30o=nar.sen60o — nv.1/2=1.√3/2 — nv=√3
18- Observe que a luz incide na face interna com ângulo i=45o — cálculo do ângulo limite nessa face — senL=nmenor/nmaior=1/n
para que ocorra reflexão total ele deve incidir com ângulo superior ao ângulo limite, ou seja i>L, ou ainda seni > senL — sen45o > senL — √2/2 > 1/n — n > √2 R- A
19- R- C (veja resolução da questão anterior)
20- a)
b) seni > senL — sen45o > senL — √2/2 > 1/n — n > √2
21- Veja figura abaixo:
para que haja reflexão total — i > L — seni > senL — sen60o > 1/n — √3/2 > 1/n — n > 2√3/3
22- Observe a figura abaixo:
R- D
23- Dados — np = 1,5 — nar = 1 — sen 6° = 0,104 e sen 9° = 0,157 — afigura a seguir ilustra a situação, mostrando a trajetória do raio até a reflexão no espelho plano — na primeira face, a incidência é normal, portanto não há desvio — a segunda face,
aplicando a lei de Snell — np sen i = nar sen r — 1,5 sen 6° = 1 sen r — 1,5 (0,104) = sen r — sen r = 0,157 — r = 9º — partir daí, acompanhando a figura, você conclui que o ângulo de reflexão no espelho plano é 3° — R- B
24-
a) Dado — nvi = 1,532 — a Fig 1 mostra a refração sofrida pelo raio violeta — lei de Snell — nvi sen 30° = nar sen θvi —
1,532 (0,5) = 1 (senqvi θvi ) — sen θvi = 0,766 — da tabela dada, θvi = 50° — na Fig 2 — a + 30° = 50° — α = 20°.
b)
c) Na refração, o desvio angular cresce do vermelho para o violeta o que pode ser provado aplicando a lei de Snell para as demais radiações envolvidas — o ângulo de incidência é θrad = 30° para todas as radiações — nrad sen 30° = nar senθar —
1.senθar = nrad. (0,5) — .senθar = nrad.(0,5) — para cada radiação (cor) envolvida — senθazul=1,528.0,5=0,764 — senθverde=1,519.0,5=0,760 — senθamarelo=1,515.0,5=0,758 — no intervalo de 0° a 90°, quanto menor o seno do ângulo, menor é o ângulo o que implica que o raio amarelo é o que sofre menor desvio, depois, nessa ordem, verde, azul e violeta — observe o esquema:
25-
26- Observe no gráfico que ambos os ângulos vão aumentando até que, a refração acontece quando θr=90o (ângulo critico) e, nesse caso θr=30o — alicando a lei de Snell-Descartes — ni.sen θi = nar.sen θr — ni.sen30o=1.sen90o — ni.1/2=1.1 — ni=2.
27- Observe a figura abaixo que mostra a luz entrando e saindo de uma gota de chuva — nesta figura, em 1 ocorre refração, em
2 reflexão, e em 3 nova refração — entre 1 e 2, ocorre dispersão — R- A