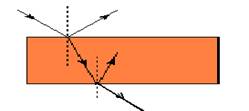
Lâminas de faces paralelas – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Lâminas de faces paralelas
01- Lei de Snell-Descartes – A relação entre o seno do ângulo de incidência e o seno do ângulo de refração é uma grandeza constante denominada índice de refração do segundo meio em relação ao primeiro, ou seja, seni/senr=n2/n1
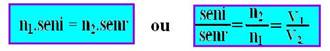
As expressões acima nos mostram que quando a luz passar de um meio menos refringente (menor indice de refração) para um meio mais refringente (maior índice de refração), o ângulo de refração será menor que o ângulo de incidência (ele se aproxima da normal) e menor será a velocidade da luz nele — no caso do exercício, veja na figura fornecida que θ1 > θ2, o que implica que nB > nA — assim, VA > VB — R- A.
02- Aplicando Snell-Descartes — nar.seni=nlâmina.senr — 1.√2/2=√2.senr — senr=1/2 — r=30o — aplicando a fórmula do desvio latera — d=e.sen(i – r)/cosr — d=1,4.sen(45 – 30)/cos30o — d=0,364/0,86 — d=0,42cm.
03- A imagem de um objeto vista através de uma lâmina de faces paralelas (placa de vidro no ar) é sempre virtual e está sempre mais próxima da lâmina que o objeto, pois ao penetrarem na lâmina os raios de luz se aproximam da normal.
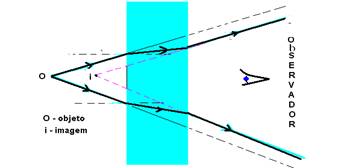
R- B
04- Um observador que vê um peixe dentro de um aquário enxerga-o mais próximo da parede do aquário
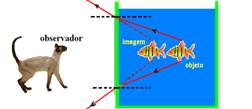
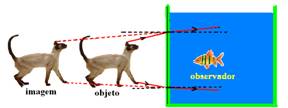
Ao mesmo tempo, o peixe vê o observador mais distante do aquário. — R- A
05- R- D — os raios incidente e emergente são paralelos e, portanto, os ângulos a e g são iguais.
06- Os ângulos incidente e emergente são iguais porque os prolongamentos dos raios incidente e emergente são paralelos
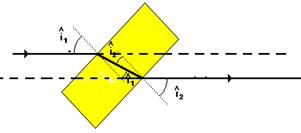
R- A
07- Veja a figura abaixo:
Se o raio de luz sofrer reflexão e refração em ambas as faces e, nelas, retornar ao ar, os seguintes ângulos serão iguais:
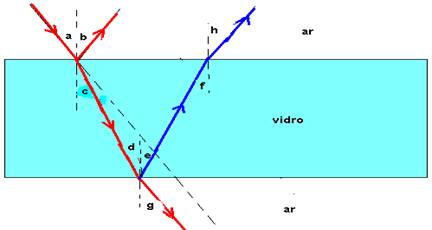
a=b=g=h c=d=e=f — R- a=qi, b=qr e l=qi
08- O desvio angular é nulo, pois não há mudança de direção dos raios incidentes e emergentes
R- A
09- Como o raio de luz incide perpendicularmente, ele não sofre desvio — cálculo da velocidade do raio de luz no interior do vidro
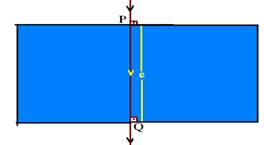
Nvidro=C/Vvidro — 1,5=3.108/Vvidro — Vvidro=2.108m/s — para percorrer e=PQ com V=2.108m/s, a luz demora t=10-10s — V=e/t — 2.108=e/10-10 — e=2.10-2m=2,0cm
10- a)
b)Aplicando Snell-Descartes na face superior — n(ar).seni=n(vidro).senr — 1.0,9=1,5.senr — senr=0,6 — sen2r + cos2r=1 —
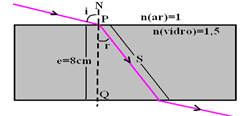
– (0,6)2+ cos2r=1 — cosr=0,8 — cosr=cateto adjacente/hipotenusa — 0.8=0.08/S — S==0,1m — cálculo da velocidade da luz no vidro — nvidro=C/Vvidro — 1,5=3.108/Vvidro0,5.10-9 — Vvidro=2,0.108m/s — Vvidro=S/t — 2.108=10-1/t — t=10-1/2.108 —
t=5,0.10-10s
11- R- D – diferentes cores sofrem desvios diferentes e, consequentemente, deslocamentos paralelos diferentes
12- Veja figura abaixo:
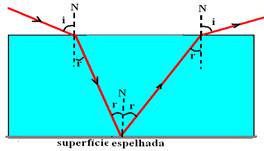
R- B
13- Observe a figura abaixo:
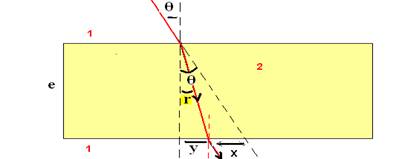
θ=30o — tg30o=√3/3 — tg30o=cateto oposto/cateto adjacente — √3/3=(1 + y)/2√3 — y=1cm — se X=Y=1cm – 2θ=r — 2.30o=r — r=15o — aplicando Snell-Descartes na face superior — n1.sen30o=n2.sen15o — 1.0,5=n2.0,26 — n2=1,9
14- Quando a luz se refrata de um meio de menor índice de refração para outro de maior índice de refração, o raio refratado se aproxima da normal — R- B
15- R- nA< nB > nC – Veja justificativa da questão anterior
16- R- B – — I vidro/II água – sofre refração quando passa do meio mais refringente para o menos refringente — II água/III ar – sofre reflexão total quando passa do meio mais refringente para o menos refringente.
17- Como a imagem está acima do observador, ela estará mais próxima do mesmo e, devido ao campo visual maior dará ao observador a impressão de ser maior que o objeto R- D
18- (01) Falsa – eles possuem a mesma direção, ou seja, são paralelos.
(02) nar.sen60o=n.senr — 1.√3/2=√3.senr — senr=1/2 — r=30o – correta.
(04) d=e.sen(i – r)/cosr — d=2√3.sen(60o – 30o)/cos30o — d=(2√3.1/2)/√3/2 — d=2cm – correta
(08) Correta — n=C/V — como C é constante, n é inversamente proporcional a V.
(16) Correta – em toda incidência normal, o raio de luz não sofre desvio.
19- Interface n1 – n2 — n1.sen θ1=n2.senr — 2.sen θ1=1,5.senr — senr=2.sen θ1/1,5 I
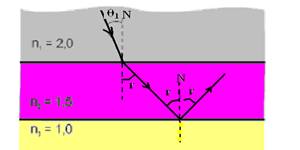
Interface n2 – ar — cálculo do ângulo limite L — senL=nmenor/nmaior=1/1,5 — para que haja reflexão total nessa interface o raio de luz deve incidir nela com um ângulo r tal que r>L, ou seja, senr>senL — senr>1/1,5 II — substituindo I em II —
2.sen θ1/1,5 > 1/1,5 — sen θ1>1/2 — θ1>30o — para qualquer valor de θ1 maior que 30o, o raio de luz sofrerá reflexão total na interface n2 – n1.
20- Observe a figura abaixo:
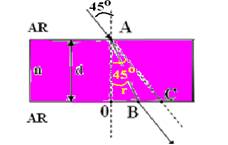
tg45o=OC/d — 1=(1 + OB)/4 — 4=1 + OB — OB=3cm — (AB)2= d2 + (OB)2 — (AB)2= (4)2 + (3)2 — AB=5cm — senr=OB/AB — senr=3/5 — aplicando Snell-Descartes na face superior — nar.sen45o=n.senr — 1.√2/2=n.3/5 — n=5√2/6
21- Lei de Snell — n1.seni = n2.senr — (1).(√3/ 2) = (√3).senr — sen r =1/2 — r = 30 º — no interior da lâmina você obtém um
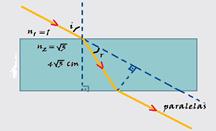
triangulo retângulo — d = cateto oposto — 4√3 = cateto adjacente — tg30o=cateto oposto/cateto adjacente — tg30o=d / 4 √3 — d / 4 √3 = √3 / 3 — 3d = 4.√3.√3 — d = 12/3 — d = 4 cm
22- nar=1 — nvidro = 
— e = cm — como o ângulo entre o raio e a lâmina é de 30°, o ângulo de incidência é: i = 60° —
o raio provem do ar, atravessa a lâmina e volta para o ar, o raio emergente é paralelo ao incidente — i’ = i = 60° — observe a
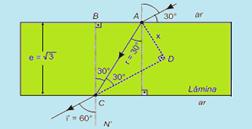
figura — lei de Snell na primeira face — nar sen i = nvidro sen r — (1) sen 60° = senr — √3/2 = √3sen r — sem r = ½ —
r = 30o — no ponto C — os ângulos 
e r são alternos-internos — = 30° — os ângulos 
e i’ são opostos pelo vértice — = 60° — = + 
— 60° = 30° + — = 30° — no triângulo ABC — cós 30o=BC/AC — √3/2 = √3/AC — AC=2cm — no triângulo ACD — sen30o=AD/AC — 1/2=x/2 — x=1cm
23- Observe o trajeto feito pelo raio luminoso — os ângulos 1 e 2 são iguais (alternos internos) — os ângulos 2 e 3 são iguais
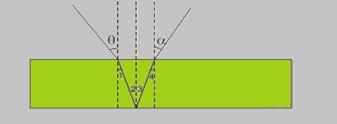
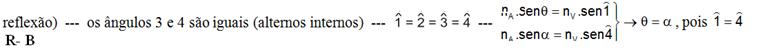
24-(UEMG-MG)
A frequência é característica da onda (no caso, luz) — quando a luz de determinada frequência se refrata passando de um meio para outro, sua velocidade de propagação e seu comprimento de onda variam, mas sua frequência permanece a mesma, independente do meio em que estiver se propagando — assim, as alternativas A, B e C estão erradas.
A correta é a D, pois, quanto mais refringente é o meio, maior será o valor de seu índice de refração n, menor a velocidade da luz nesse meio e maior será o desvio sofrido.
25-(PUC-RJ)
Aplicando a lei de Snell — n1.senθ1 = n2.senθ2 — 1.sen60o = √3.sen.θ2 — 1.√3/2 = √3.sen θ2 — sen θ2=1/2 — θ2=30o —
R- A.