Lâminas de faces paralelas
Lâminas de faces paralelas
Comportamento óptico de uma lâmina de faces paralelas
Considere um raio de luz se propagando num meio 1 de índice de refração n1 e incidindo numa lâmina de faces paralelas de material de índice de refração n2.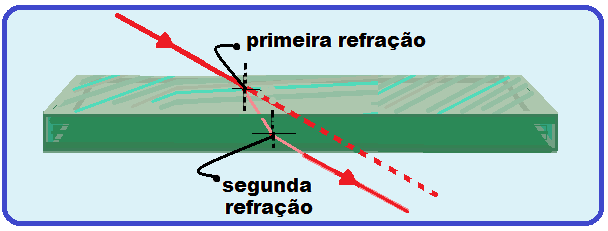
Esse raio de luz sofre duas refrações, uma quando entra na lâmina e outra quando sai dela, fazendo com que a luz seja desviada sem alterar sua direção de propagação (veja que os raios de luz incidente e emergente são paralelos).
Exemplos de lâminas de faces paralelas: vidros de: uma vidraça, uma estufa, uma cobertura, para-


brisa de um carro, moldura de vidro de um quadro, etc.
Equação do desvio lateral de um raio de luz ao atravessar uma lâmina de faces paralelas
Na figura abaixo temos uma lâmina de faces paralelas de índice de refração n2, imersa num meio
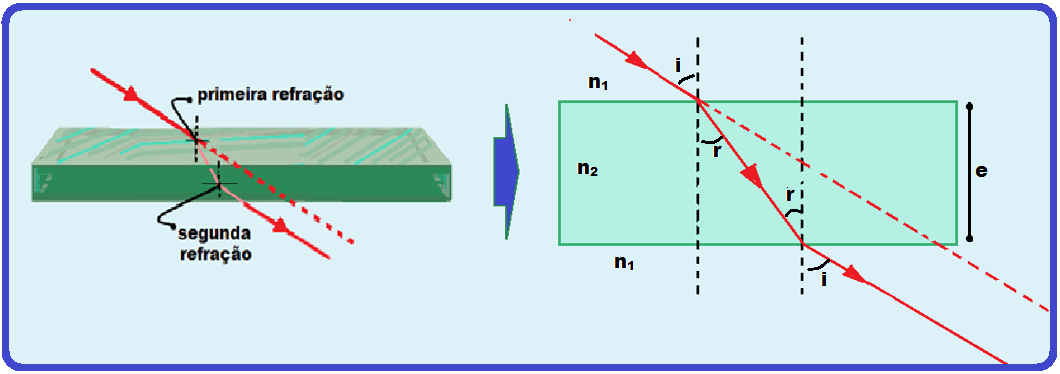
de índice de refração n1 e sendo atravessada por um raio de luz monocromático.
Aplicando a lei de Snell Descartes nas duas refrações da figura:
1a refração ![]() entrando na lâmina
entrando na lâmina ![]() n1.sen i = n2.sen r
n1.sen i = n2.sen r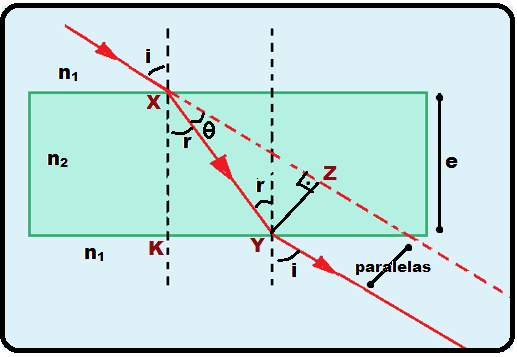
2a refração ![]() saindo da lâmina
saindo da lâmina ![]() n2.sen r = n1.sen i
n2.sen r = n1.sen i
Não existe desvio angular que é nulo, pois os raios incidente e emergente são paralelos, mas sim desvio lateral (d) que corresponde à distância entre as retas que contém os raios incidente (seu prolongamento) e emergente.
Cálculo do desvio (d):
Triângulo XYZ ![]() sen θ = d/XY
sen θ = d/XY ![]() sen θ = sen (i – r) = d/XY
sen θ = sen (i – r) = d/XY ![]() XY = sen (i – r)/d (I).
XY = sen (i – r)/d (I).
Triângulo KXY ![]() cos r = e/XY
cos r = e/XY ![]() XY = cos r/e (II).
XY = cos r/e (II).

O que você deve saber, informações e dicas
![]()
Observe na expressão do desvio lateral que, quanto maior for a espessura e da lâmina, maior será

o desvio sofrido.
![]()
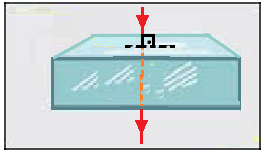
Se o raio incidente na lâmina for perpendicular a uma de suas faces o desvio lateral será nulo. A incidência normal ocorre sem desvio do raio de luz.
![]()
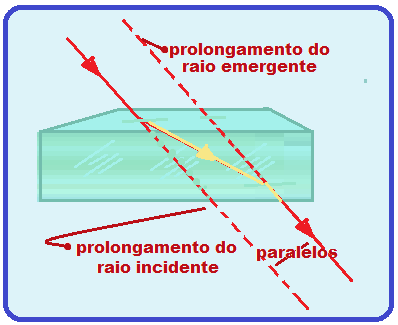
Os prolongamentos dos raios incidente e emergente são sempre retas paralelas.
A imagem de um objeto vista através de uma lâmina de faces paralelas (placa de vidro no ar) é sempre virtual e está sempre mais próxima da lâmina que o objeto, pois ao penetrarem na lâmina os raios de luz se aproximam da normal.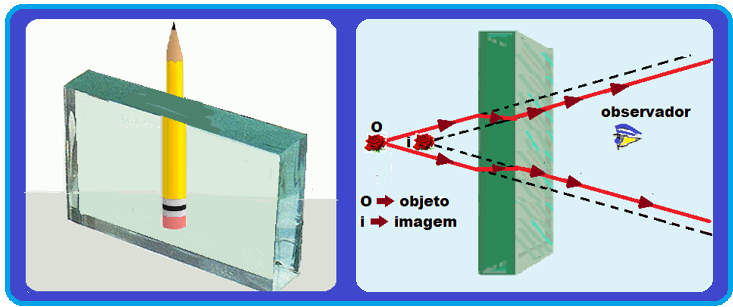
Assim, a imagem é vista pelo observador como sendo maior que o objeto por estar mais próxima (aumenta o campo visual).
![]()
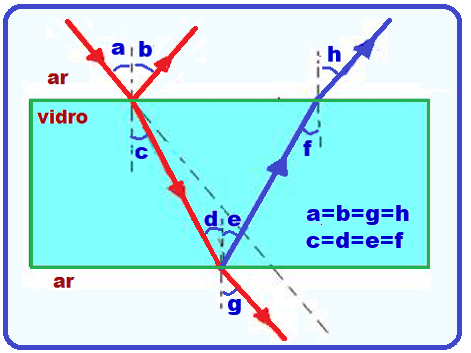
Se o raio de luz sofrer reflexão e refração em ambas as faces e, nelas, retornar ao ar, os seguintes ângulos serão iguais a = b = g = h e c = d = e = f.
![]()
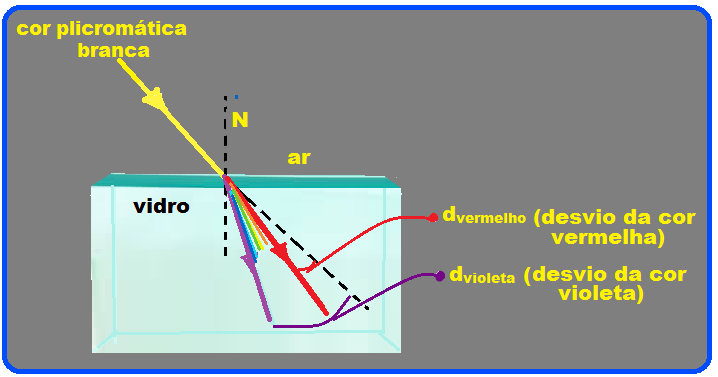
Podemos também decompor uma luz policromática fazendo-a atravessar uma lâmina de vidro de faces paralelas.
No interior da lâmina cada cor se move com velocidades diferentes e ao saírem da mesma sofrerão desvios laterais diferentes, sofrendo assim, dispersão.
A cor que sofre menor desvio ao penetrar no vidro é o vermelho (maior velocidade) e menor desvio é o violeta (maior velocidade).
![]()
Associação de lâminas de faces paralelas
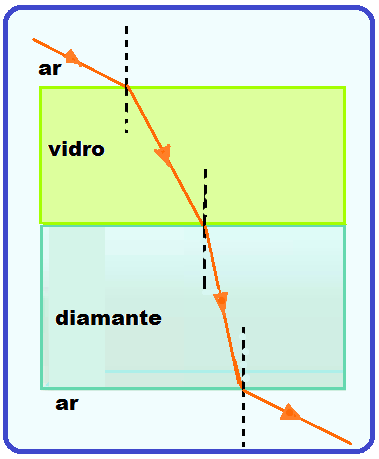
Considere as duas lâminas da figura, imersas no ar, uma de vidro e a outra de diamante
O índice de refração do diamante é maior que o do vidro, que por sua vez é maior que o do ar.
Observe que, quanto mais refringente for o meio (maior índice de refração), mais o raio de luz se aproxima da normal,
menor será a velocidade da luz nesse meio e maior será o desvio sofrido.
![]()
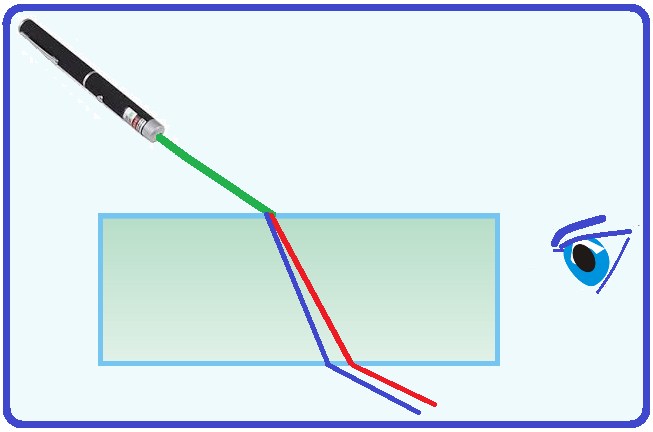
Tem-se um aparelho que emite um feixe colimado, estreito, de luz verde. Mas o feixe é, na verdade,
mistura de luz amarela com azul.
Pode-se descobrir tal fato, fazendo-se incidir o feixe numa lâmina de vidro de faces paralelas e assim uma das cores sofreria um deslocamento paralelo maior que a outra, numa incidência oblíqua.
Diferentes cores sofrem desvios diferentes e, consequentemente, deslocamentos paralelos diferentes
![]()
Veja um exercício de aplicação sobre desvio lateral nas lâminas de faces paralelas:
A espessura de uma lâmina de vidro de faces paralelas é de 2,0 cm.
Um raio monocromático de luz incide numa de suas faces com ângulo de 60o e se refrata com ângulo de 45o.
Considerando cos75o = sen15o = 0,25, sen60o = cos30o = √3/2 = 0,8, nar = 1,0 e sen45o = cos45o = √2/2 = 0,7, pede-se:
a) Esboçar o trajeto do raio de luz ao atravessar a lâmina
b) Determinar o índice de refração do vidro
c) Determinar o desvio lateral (d) e o desvio angular (β)
d) Determinar o valor do ângulo de emergência
a)
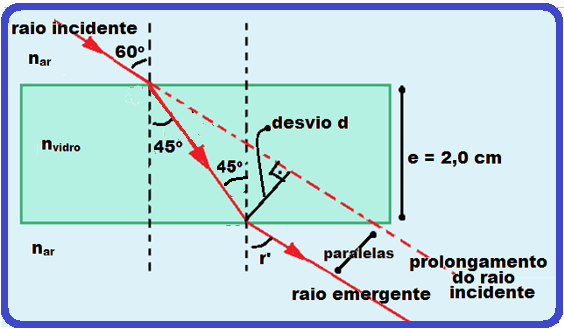
![]()
nvidro = 1,2.
c) d = e.sen(i – r)/cosr ![]() d = 2.sen(60o – 45o )/cos45o
d = 2.sen(60o – 45o )/cos45o ![]() d = 2.sen(15o)/cos45o
d = 2.sen(15o)/cos45o ![]() d = 2.0,25/0,7
d = 2.0,25/0,7 ![]() d = 0,71cm (desvio lateral)
d = 0,71cm (desvio lateral) ![]() o desvio angular é nulo, pois o prolongamento do raio incidente e o raio emergente tem a mesma direção, ou seja, são paralelos
o desvio angular é nulo, pois o prolongamento do raio incidente e o raio emergente tem a mesma direção, ou seja, são paralelos ![]() β = 0.
β = 0.
d) Aplicando Snell-Descartes na face inferior da lâmina ![]() nvidro.senr = nar.senr’
nvidro.senr = nar.senr’ ![]() 1,2.sen45o = 1.senr’
1,2.sen45o = 1.senr’ ![]() 1,2.0,7 = 1.senr’
1,2.0,7 = 1.senr’ ![]() senr’ = 0,8
senr’ = 0,8 ![]() r’ = 60o
r’ = 60o ![]() observe que i = r’ = 60o (por essa razão que o raio incidente e o prolongamento do raio incidente são paralelos).
observe que i = r’ = 60o (por essa razão que o raio incidente e o prolongamento do raio incidente são paralelos).
