Equação dos Fabricantes de Lentes – Resolução
Resolução dos exercícios de vestibulares sobre
Equação dos Fabricantes de Lentes
01- C1=1/f1=1/5.10-2 — C1=20di — C2=1/f2=1/15.10-2 — C2= 6,7di — Ceq=C1 + C2=20 + 6,7 — Ceq=26,7di — Ceq=1/feq — 26,7=1/feq — feq=3,7cm
02- C1=1/f1=1/10.10-2 — C1=10di — C2=1/f2=1/40.10-2 — C2= 2,5di — Ceq=C1 + C2=10 + 2,5 — Ceq=12,5di — R- D
03- Ceq= C1 + C2 — 1/feq=1/f1 + 1/f2 — 1/feq=(f2 + f1)/f1.f2 — feq=f1.f2/(f1 + f2) — R- B
04- Lente convergente – C1=+12di — C2= – 20di — Ceq= +12di – 20di — Ceq= – 8di — divergente, pois ceq é negativo.
05- a) Trata-se de uma lente convergente (bordas finas) de índice de refração em relação ao ar – nlente/nar=1,35 — face convexa – Rc=2,5.10-3 m — face plana Rp=∞ — equação dos fabricantes de lentes C=1/f=((nlente/nar – 1).(1/Rc + 1/Rp) — C=1,35 – 1,00).(1/2,5.10-3 +1/∞) — C=(0,35).(0,4.103 + 0) — C=140di
b) Se a imagem é direita — i=50.O — i/O=-P’/P — 50.O/O=-P’/P — P’=-50P — 1/f=140m — 1/f=1/P + 1/P’ — 140=1/P – 1/50P — 140=49/50P — P=0,007m=7mm
06- nv=1,5 — nar=1,0 — Rc=2.10-2m — Rp=∞ — equação dos fabricantes de lente — 1/f=C=(nv – nar).(1/Rc + 1/Rp) —
1/f=(1,5 – 1,0).(1/2.10-2 + 0) — 1/f=25m — P’=-36cm=-36.10-2m (negativa-imagem virtual-lente divergente) — 1/f=1/P + 1/P’ — 25=1/P – 1/36.10-2 — 25 + 1/36.10-2=1/P — P=0,04m — i=20.10-2 m (positiva – direita) — i/O=-P’/P —
20.10-2/O=-(-36.10-2)/4.10-2 — O=2.10-2m — O=2cm — R- D
07- I- 1/f=(nl/nm – 1).(1/R1 + 1/R2) — (1/R1 + 1/R2) é constante — 1/f=(nl/nm – 1). (constante) — observe nesta expressão que, como (nl/nm – 1) é inversamente proporcional a f, quanto maior for a razão nl/nm, menor será a distância focal da lente — Falsa
II- Se (nl/nm – 1) é inversamente proporcional a f, se nl aumenta, o conjunto (nl/nm – 1) diminui e como ele é inversamente proporcional a f, f aumenta — Verdadeira
III- Verdadeira, veja justificativa anterior.
R- C
08- C=(1,5 – 1).(1/Rconvexa + 1/Rplana) — C=(0,5).(1/20.10-2 + 1/∞) — C=(0,5).(1/20.10-2 – 0) — C=2,5di — R- E
09- Antes de a lente ser partida, duas faces convexas de raio R
![]()
1/f=(n-1).(1/R1+1/R2) — 1/f=(1,8-1).(1/R+1/R) — 1/f=(0,8).2/R — R=1,6f I
Depois de partida, o índice de refração da lente (n=1,8) continua o mesmo — uma face plana de raio ∞ e outra convexa de raio R
![]()
1/f=(n-1).(1/R1+1/R2) — 1/f1=(1,8-1).(1/R+1/∞) — 1/f1=(0,8).(1/R + 0) — f1=R/0,8 — R=0,8f1 II
Igualando I com II — 1,6f=0,8f1 — f1=2f — R- E
10- No ar — Car=(nlente/nar – 1)(1/R + 1/∞) — 1=(nlente/1 – 1).(1/0,5 + 0) — 1=(nlente 1).2 — nlente=1,5
Na água — Cágua=(nlente/nágua – 1)(1/R + 1/∞) — Cágua=(1,5/(4/3) – 1)(1/R + 1/∞) — Cágua=(4,5/4 – 1)(1/0,5 + 0) —
Cágua=(0,125).2 — Cágua=0,25 — R- A
11- Cálculo da convergência da lente — C=(nágua/nar – 1). (1/Rc + 1/Rp) — C=(1,3/1 – 1). (1/3.10-3 + 1/∞) — C=102m —
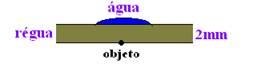
f=1/C — f=10-2m — P=2.10-3m — 1/f=1/P + 1/P’ — 1/10-2=1/2.10-3 + 1/P’ — 102 – 2.103=1/P’ — 102 – 20.102=1/P’ —
P’= – 1/19.10-2m — A= – P’/P= – (- 1/19.10-2)/2.10-3 — A=0,26 — R- A
12- C=(1,5/1 – 1).(1/6.10-2 + 1/∞) — C=(0,5).102/6 — C=50/6m — f=1/C=6/50=0,12m — f=12,0cm
13- A grama deve estar no foco da lente — 1/f=(n-1)[(1/R1)+(1/R2)] — 1/f=(1,5-1)[(1/0,1)+(1/∞)] — 1/f=5m — f=1/5=0,2m=20cm — R- D
14- a) A distância focal, onde ele concentra os raios de luz é de f=10cm=0,1m — 1/f=(n-1)[(1/R1)+(1/R2)] — 1/0,1=(n-1)[(1/R)+(1/R)] — 10=(n – 1).2/R — R=0,2.(n-1), onde n é o índice de refração da lente
b) i=3.o — i/o=-P’/P — 3.0/o= – P’/P — 3= – P’/P — P’= – 3P — 1/f=1/P + 1/P’ — 1/f=1/P – 1/3P — 1/10=(3 – 1)/3P — P=20/3 = 6,7cm
15- C=1/f=(n-1)[(1/R1)+(1/R2)] — C=(1,5 – 1).(1/2,5.10-3 + 1/∞) — C=0,5. 400 — C=200di — R- E
16-
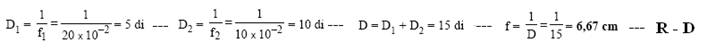
17- Os focos de luz encontram-se no foco de cada lente — Vermelha — 1/fv=(1,6 -1).(1/1 + 1/1) — fv=1/1,2=0,83m — 1/fvi=(1,64 – 1).(1/1 + 1/1) — fvi=1/1,28 — fvi=0,78m — d=0,83 – 0,78 — d=0,05m=5cm
18-
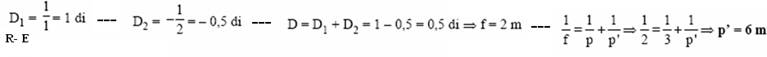
19- Primeiro caso

— fe=12cm — d=10cm — 1/fe= 1/f1 + 1/f2 – d/f1.f2. — 1/12=1/f1 + 1/f2 – 10/f1.f2 — f1.f2=12f2 + 12f1 – 120 —
f1.f2=12(f1 + f2) – 120 I
Segundo caso

— fe=60/7cm — d=0 (justapostas) — 1/fe= 1/f1 + 1/f2 – d/f1.f2 — 7/60=.1/f1 + 1/f2– 0/f1.f2 — 7/60=1/f1 + 1/f2 — 7f1.f2=60f2 + 60f1 — f1.f2=60.(f1 + f2)/7 II — igualando I com II — 12(f1 + f2) – 120 = f1.f2=60.(f1 + f2)/7 — 84(f1 + f2 – 840=60.(f1+ f2) — 24.(f1 + f2)=840 — f1 + f2=35 III — III em I — f1.f2=12.35 – 120 — f1.f2=420 – 120 — f1.f2=300 VI
Observe o sistema composto por III e IV, cujo produto é 300 e cuja soma é 35 e assim, esses números são — f1=15cm e f2=20cm ou f2=20cm e f1=15cm
20- I- Correta — trata-se de uma lente convergente, pois essa lente tem extremidades finas e está imersa no ar, assim é convergente e nesse caso o objeto está entre fo e o centro óptico O da lente — a imagem tem as seguintes cacterísticas:
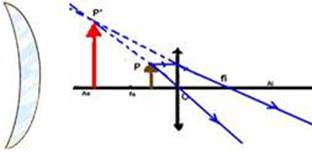
Natureza: Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos.
Localização: Antes de foco
Tamanho e orientação: Maior que o objeto e direita em relação a ele.
Utilidade – Lupa (lente de aumento) e microscópios.
II.Correta — observe nas figuras que o aumento da figura 1 é maior que o aumento da figura 2 (lente resultante) e que, em ambos os casos a imagem é aumentada — assim, a lente 1 e a lente equivalente são convergentes — A1>Aeq — quando justapomos duas lentes
obtemos uma lente equivalente cuja vergência ou convergência Ceq é a soma algébrica da vergência de cada uma das lentes, ou seja, Ceq=C1+ C2 — lembre-se de que C=1/f e que se a lente é divergente f e C são negativos e se a lente é convergente, positivos — no caso do exercício — Ceq>0 (convergente) — C1>0 (convergente) — quanto maior o aumento, maior a vergência — se C1>Ceq – (A1>Aeq) — Cx(justaposta a C1) — Ceq = C1 + Cx — (Ceq – C1)=Cx — nessa expressão, Cx deverá ser negativo pois C1>Ceq — se a vergência é negativa a lente x é divergente o que é o caso da lente plano côncava.
III. Falsa — do item II — Ceq<C1 — 1/feq < 1f1 — f1 < feq.
R- A
