Fórmula (equação) dos Fabricantes de Lentes

Fórmula (equação) dos Fabricantes de Lentes

Podemos determinar a distância focal f e a vergência C de uma lente conhecendo os raios de curvatura de suas faces e os índices de refração da lente e do meio que a envolve, através da equação dos fabricantes de lentes:

    

Considerações importantes para a resolução de exercícios

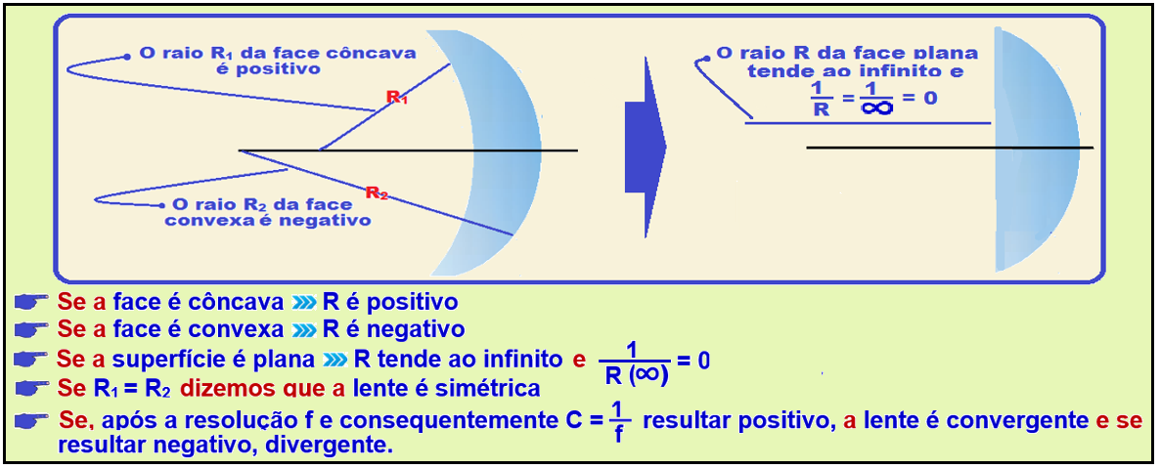
Recordando:

 

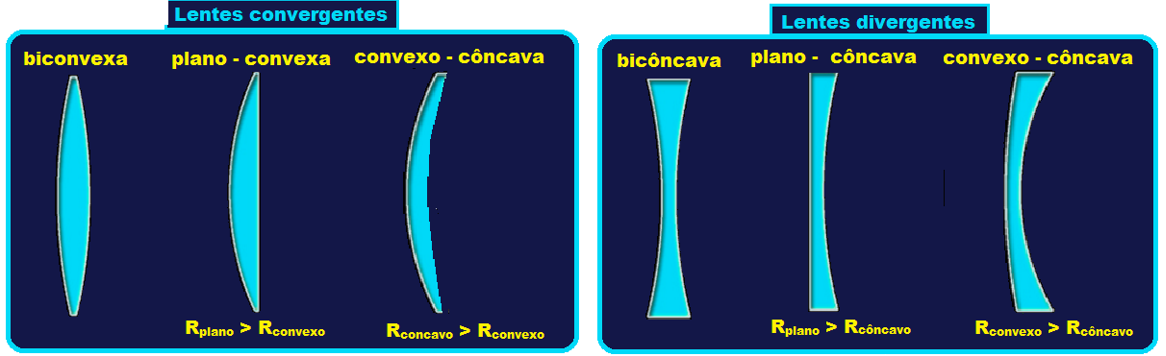
Justaposição de lentes

Quando justapomos duas lentes obtemos uma lente equivalente cuja vergência ou convergência C_eq é a soma algébrica da vergência de cada uma das lentes, ou seja, C_eq = C₁+ C₂.

Lembre-se que C = 1 / f e que se a lente é divergente f e C são negativos e se a lente é convergente, positivos.

Exemplo numérico:

Uma lente convergente de 12di é justaposta a uma lente divergente de 20di.

A associação funciona como uma única lente convergente ou divergente? Determine sua vergência.

Resolução:

Lente convergente C₁ = +12di. 

Lente divergente C₂ = – 20di.

C_eq = + 12di – 20di    C_eq = – 8di.

Essa associação funciona como uma única lente divergente, pois C_eq é negativa.

O que você deve saber, informações e dicas

 

 Quando uma lente quebra, a distância focal e consequentemente a vergência de cada pedaço não se altera, pois baseado na equação dos fabricantes, as superfícies externas continuam com os mesmos raios e a lente continua com mesmo índice de refração 

 

Observe na expressão C = 1/f = (n_l/n_m – 1).(1/R₁ + 1/R₂) onde n_l é o índice de refração da lente e n_m o índice de refração do meio que a envolve, que:

se a lente estiver imersa no ar (n_m = 1), a expressão C =1/f = (n_l/n_m – 1).(1/R_{1 +} 1/R₂)  fica C = 1/f = (n_l – 1).(1/R_{1 +} 1/R₂).

Assim, se a lente possuir os mesmos raios, f é inversamente proporcional a (n_l – 1), ou seja, quanto maior for o índice de refração da lente, menor será sua distância focal.

como (n_l/n_m – 1) é inversamente proporcional a f, quanto maior for a razão n_l/n_m, menor será a distância focal da lente.

 

Analise as resoluções dessas questões interessantes:

01-(ITA) Uma lente convergente biconvexa tem distância focal de 20cm quando está mergulhada em

ar.

A lente é feita de vidro, cujo índice de refração é n_v = 1,6. Se a lente é mergulhada em um meio, menos refringente do que o material da lente, cujo índice de refração é n_m, considere as seguintes afirmações e analise-as como verdadeiras ou falsas:

I. A distância focal não varia se o índice de refração do meio for igual ao do material da lente.

II. A distância focal torna-se maior se o índice de refração n_m for maior que o do ar.

III. Neste exemplo, uma maior diferença entre os índices de refração do material da lente e do meio implica numa menor distância focal.

III- Verdadeira, veja justificativa anterior.

02-(UFC-CE) Uma lente esférica delgada, constituída de material de índice de refração n, está imersa no ar (n_ar=1,00).

A lente tem distância focal f e suas superfícies esféricas tem raios de curvatura R₁ e R₂.

Esses parâmetros obedecem a uma relação, conhecida como “equação dos fabricantes”, mostrada abaixo.

                                                       1/f=(n-1).(1/R₁+1/R₂)   

Suponha uma lente biconvexa de raios de curvatura iguais (R₁ = R₂ = R), distância focal f e índice de refração n = 1,8 (figura 1).

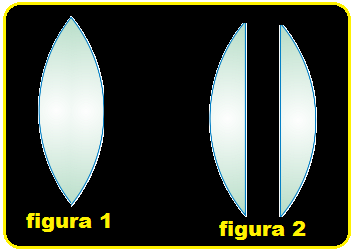
Essa lente é partida dando origem a duas lentes plano-convexas iguais (figura 2).

Calcule o valor da distância focal de cada uma das novas lentes.

Resolução:

Antes de a lente ser partida, ela possui duas faces convexas de raio R tal que, pela equação dos fabricantes fornece o valor do raio R em função da distância focal f 1/f = (n – 1).(1/R₁ + 1/R₂)   1/f=(1,8-1).(1/R+1/R)    1/f=(0,8).2/R    R=1,6f (I)       

 

Confira os exercícios com resolução comentada