Resolução comentada dos exercícios de vestibulares sobre Estudo Analítico dos Espelhos Esféricos
Resolução comentada dos exercícios de vestibulares sobre
Estudo Analítico dos Espelhos Esféricos
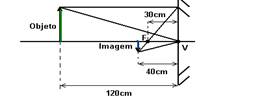
01- a) P’=+40cm (real) — f=+30cm (côncavo) i= -3cm (invertida) — 1/f=1/P + 1/P’ — 1/30=1/P + 1/40 — 1/P = 1/30 – 1/40 — (4 – 3)/120 = 1/P — P=120cm
b)
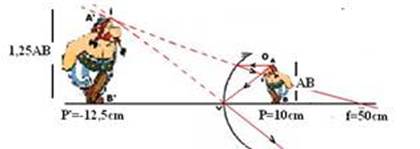
02- f=-40cm espelho convexo) — espelho convexo a imagem é direita e i e O tem mesmo sinal — O=20i — i/O=-P’/P —
i/20i=-P’/P — P=-20P’ — 1/f = 1/P + 1/P’ — 1/-40 = 1/-20P’ + 1/P’ — -1/40 = 19/20P’ — 20P’P=-760 — P’=-38cm — P=-20P’ — P=(-20).(-38)=760cm — P=7,6m R- C
03- a) O espelho, para obter a maior intensidade de radiação solar possível, deve ter 60m de raio de curvatura, de modo que o navio fique em seu foco quando estiver a 30m da praia.
b) Intensidade de radiação = Potência/área — I=P/S — 60% de I=0,6.500 — I=300W/m2 — cada espelho tem área —
S=0,5.1,0 — S=0,5m2 — como são 60 espelhos — St=60.0,5 — St=30m2 — I=P/St — 300=P/30 — P=9.000W ou P=9kW
04- O=h — P=15cm — sendo a imagem direita e menor que o objeto a imagem é virtual e o espelho é convexo e i=h/5 —
i/O=-P’/P — (h/5)/h=-P’/15 — P’=-3cm — 1/f = 1/P + 1/P’ — 1/f=1/15 + 1/-3 — f=-3,75cm — R=2.(-3,75) —
R=-7,5cm e o sinal negativo significa que o espelho é convexo R- C
05- Situação inicial (t=0) — P=50cm — f=10cm — 1/f=1/P+1/P’ — 1/10=1/50+1/P’ — 1/10 – 1/50=1/P’ — 4/50=1/P’ — P’=12,5cm (posição inicial da imagem)
Situação final (t=5s) — V=ΔS/Δt — 4= ΔS/5 — ΔS=20cm — como ele se aproxima do espelho sua nova distância do vértice do espelho será — P=50 – 20 — P=30cm — f=10cm — 1/10 = 1/30 + 1/P’ — P’= 15cm (nova posição da imagem) — A imagem percorreu ΔS=15 – 12,5 — ΔS=2,5cm — R- E
06- O=1m — espelho convexo – a imagem é virtual, direita e menor que o objeto — O=4i — P=1,2m — i/O=-P’/P — i/4i=-P’/1,2 — P’= – 0,3m — 1/f = 1/P + 1/P’ — 1/f=1/1,2 + 1/-0,3 — f= -1,2/3 — f= – 0,4m (o sinal negativo significa que o espelho é convexo)
07- a) Espelho convexo e a imagem é virtual, direita e menor que o objeto. (tem a vantagem de aumentar o campo visual).
b) f=-0,25m (espelho convexo) — O=1,6m — P=2,25m —1/f=1/P + 1/P’ — -1/0,25=1/2,25 + 1/P’ — P’= -0,225m —
i/O=-P’/P — i/1,6=-(-0,225)/2,25 — i=0,16m=16cm
08- Convexo — f=-10cm — P=6cm — 1/-10=1/6 + 1/P’ — P’= -3,75cm — i/O=-P’/P — 1,5/O=-(-3,75)/6 — O=2,4cm — côncavo — f=10cm — i=-1,5m (imagem invertida) — O=2,4cm — i/O=-P’/P — -1,5/2,4=-P’/P —
P’=0,625P — 1/10=1/P + 1/0,625P — P=16,25/0,625 — P=26cm R- C
09- Situação inicial (t=0) — como o objeto está sobre C, a imagem estará sob C e P’=6m (figura abaixo)
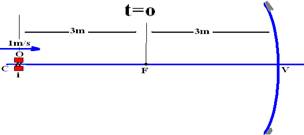
Situação final (t=2s) — V=d/t — 1=d/2 — d=2m – o objeto se deslocou 2m e está a P=6-2=4m do vértice P=4cm —
1/f=1/P + 1/P’ — 1/3=1/4 + 1/P’ — P’=12m (figura abaixo)
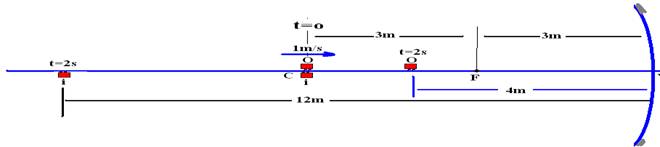
A imagem, que estava a 6m do espelho, se afastou 6m do mesmo R- B
10- A=-P’/P — 2=-P’/P — P’=-2P — 1/1=1/P – 1/2P — P=0,5m=50cm
11- a) P=30m — f=-6m (convexo) — 1/f = 1/P + 1/P’ — -1/6=1/30 + 1/P’ — P’=-5m (observe que para um objeto a 30m do espelho convexo, a imagem seria vista como se estivesse a 5m do mesmo, aparentando assim, ser menor).
b) No espelho plano a imagem é simétrica (objeto e imagem são eqüidistantes do espelho) e de mesmo tamanho do objeto – 30m
12- a) V=d/t — 5=d/2 — d=10cm
Para t = 2,0 s ë x = 10 cm. — em t = 2,0 s, o objeto estará a 40 cm do vértice do espelho, ou seja, ele estará antes do centro de curvatura C do espelho.
Para um objeto que se encontra antes do centro de curvatura de um espelho côncavo, as características da imagem formada são: real, invertida e menor.
b) Para que a imagem se forme no infinito (imagem imprópria) o objeto deve se encontrar no foco do espelho. Portanto, ele deverá percorrer d=40 cm — V=d/t — 5=40/t — t=8s.
c) Distância percorrida pelo objeto em 7 s:
V=d/t — 5=d/7 — d=35cm — logo a posição do objeto será: p = 15 cm. — calculando a posição da imagem formada usando a relação: (1/p) + (1/p’) = 1/f — utilizamos o fato de que f = R/2 —p’ = 30 cm
Em t = 7,0 s o objeto se encontra entre o foco e o Centro de Curvatura e, portanto, sua imagem será real, maior e invertida.
O cálculo do tamanho da imagem formada pode ser realizado utilizando a equação para ampliação da imagem, dada por:
A = i/o = p’/p — i/10 = – [(30)/15] — i = – 20 cm
Nesta equação i e o são os tamanhos da imagem e do objeto, respectivamente. O sinal negativo indica que a imagem formada é invertida.
13- Quando observava cravos e espinhas seu rosto estava entre o foco (1,5m) e o espelho, que fornecia uma imagem virtual, direita e maior. Quando colou seu rosto a 2m do espelho, ele ficou entre o foco e o centro de curvatura e, nesse caso, a imagem fica maior e invertida. R- B
14- a) P=4m — P’=-0,2m (imagem virtual) — 1/f = 1/P + 1/P’ — 1/f=1/4 – 1/0,2 — f=-4/19m — R=2f=2.(-4/10) —
R= (8/19) m
b) H=O=1,6m — i=h — i/O=-P’/P — h/1,6=-(-0,2)/4 — h=0,08m=8cm
15- P=90cm — O=10i — i/O=-P’/P — i/10i=-P’/90 — P’=-9cm — 1/f=1/90-1/9 — f=-10cm — em módulo f=10cm R- D
16- Antes — i=3O/4 — i/O=-P1’/P1 — (3O/4)/O = -P1’/P1 — P1’= – 3P1/4 — 1/f=1/P1 + 1/P’1 — 1/f= 1/P1 -4/3P1 —
f=-3P1 (I) — i=O/4 — i/O= -P2’/P2 — (O/4)/O=-P’2/P2 — p2’=-P2/4 — 1/f=1/P2+ 1/P2’ — 1/f=1/P2 – 4/P2 — f= -P2/3 (II) — igualando I com II — -3P1=-P2/3 — P2=9P1 R- A
17- Sendo a distância do Sol à Terra muito grande, os raios de luz emitidos por ele chegam à Terra como feixes de raios paralelos e a imagem P’ se forma no foco — P’= f =1m — P=250d — O=d
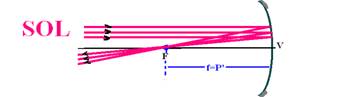
i/O = -P’/P — i/d = – 1/250d — i=-1/250=4.10-3m – R- E
18- Cálculo da imagem A’ de A, conjugada pelo espelho esférico côncavo — P=30cm — f=20cm — 1/f=1/P + 1/P’ — 1/20 – 1/30=1/P’ — P’=60cm — observe na figura abaixo que os raios de luz emitidos por A, sofrem reflexão no espelho
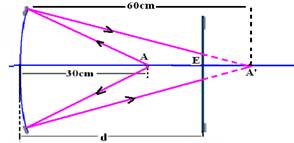
côncavo, incidem no espelho, onde são refletidos mas,a imagem se forma em A’, que se comporta como objeto virtual para o espelho plano. Os raios de luz que atingem o espelho plano devem sofrer reflexão e retornar a A.
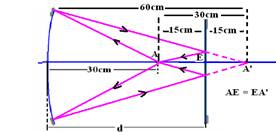
Como no espelho plano objeto e imagem são simétricos ao espelho as distâncias AE e AE’ são iguais e de 15cm cada uma. Assim, a distância pedida d vale30 + 15 — d=45cm
19- Observe na figura abaixo que, como os raios solares incidem paralelamente ao eixo principal, eles se refletem de modo que o prolongamento dos raios refletidos se encontre no foco F’, onde está a imagem do Sol, que vai servir como objeto virtual para o espelho côncavo E’’.
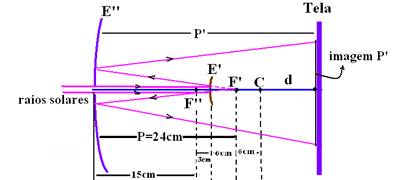
Então, para E’’, temos — P=24cm — P’ (distância da imagem do Sol projetada na tela por E’’) — f=15cm — 1/f=1/P+1/P’ — 1/15=1/24 + 1/P’ — 1/P’=(8 – 5)/120 — P’=40cm — d=40 – 30 — d=10cm
20- Ambos os espelhos são côncavos, possuindo, então, abscissas focais positivas — equação dos pontos conjugados — 1/f=1/P + 1/P’ — P´=P.f/(P – f) — espelho da esquerda (1) — f1=2m — P1=1m — P1’=1 x 2/(1 – 2) — P1’= – 2m (imagem virtual e atrás do espelho) — espelho da direita (2) — f2=5m — P2=1m — P2’=1 x 5/(1 – 5) — P2’= – 5/4 m (imagem virtual e atrás do espelho) — a figura mostra as localizações objeto e imagens em relação aos espelhos — observe que a distância D entre a
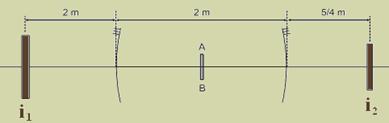
imagem da esquerda (i1) e a da direita i2 vale — D=2 + 2 + 5/4 — D=21/4 m — R- A
21- p = 10 cm — A = 5 — A= – P’/P — 5= – P’/10 — P’=-50cm — 1/f=1/P + 1/P’ — 1/f=1/10 + 1/(-50) — 1/f=(5 – 1)/50 –f=50/4 — f=12,5cm — R- A
22- h =o= 8 cm — p = 80 cm — h’ = i=1,6 cm — i/o=-P’/P — 1,6/8= – P’/80 — P’= – 16cm — 1/f=1/P + 1/P’ — 1/f=1/80 + 1/(-16) — f= – 20cm — valor absoluto — |f| = 20 cm — R- B
23- Observe que, pelo enunciado, o farolete deve emitir raios de luz paralelos quando a lâmpada estiver localizada a 10cm do espelho esférico côncavo, ou seja, ela deve estar sobre o foco, pois os raios de luz, nessa posição emergem paralelos — f=+10cm (I) —
Como a imagem é projetada e ampliada 5 vezes, a imagem é invertida em relação ao objeto e, consequentemente o aumento linear transversal é negativo — A=-5 — A=-P’/P — -5=-P’/P — P’=5P (II) — substituindo (I) e (II) na equação dos pontos conjugados — 1/f=1/p + 1/P’ — 1/10=1/P + 1/5P — P=12cm — portanto a lâmpada encontra-se 2cm adiante do foco —
R- E
24- Observe a situação descrita ilustrada na figura abaixo — como o raio refratado incide no
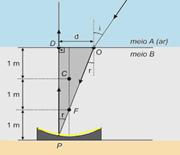
espelho passando pelo foco, ele reflete paralelo ao eixo principal — quando um ângulo é pequeno (θ < 10°), você pode fazer a aproximação — sen θ = tg θ = θ (radiano) — como nesse caso i = 7° e r < i (ângulos pequenos), você pode trocar o seno pela tangente na lei de Snell —
nA.tg i = nB.tg r — 1.(0,12)=1,2.tg r — tg r = 0,12/1,2 — tg r = 0,1 — observe no triângulo OPD hachurado da figura —
tg r = d/3 — 0,1=d/3 — d=0,3m
25- Dados: f=R/2=1/2=0,5m=50cm — P=50 + 10=60cm — equação dos pontos conjugados de
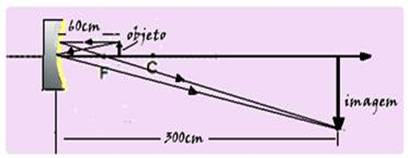
Gauss — 1/f=1/P + 1/P’ — 1/50=1/60 + 1/P’ — 1/50 – 1/60=1/P’ — (6 – 5)/300=1/P’ — P’=300cm — distância entre objeto e imagem — d=300 – 60=240cm — R- A
26- A distância focal do espelho é igual à metade de seu raio de curvatura — f=+1/2m — f= + 50cm (positiva porque o espelho é côncavo) — quando o lápis estiver a 10cm do espelho – P=10cm — equação dos pontos conjugados de Gauss — 1/f=1/P + 1/P’ — 1/50 – 1/10=1/P’ — (1 – 5)/50=1/P’ — 4P’=-50 — P’= – 12,5cm (a imagem é virtual e está atrás do espelho e a
12,5cm dele) — A= -P’/P=-(-12,5)/10 — A=1,25 (a imagem é direita A>0 e 1,25 vezes maior que o objeto).
Segunda etapa — distância (P) em que o lápis deveria estar do vértice do espelho, para que sua imagem fosse direita e ampliada cinco vezes — A=+5 (imagem direita A>0) — A= – P’/P — 5= – P’/P — P’=-5P — 1/f=1/P + 1/P’ — 1/50=1/P + 1/(-5P).
1/50=1/P – 1/5P — 1/50=4/5P — 5P=200 — P=40cm