Estudo Analítico das Lentes Esféricas
Estudo analítico dos espelhos esféricos
Como você já viu no capítulo anterior, é possível determinar graficamente as características da imagem conjugada por um dado espelho esférico.
Mas, existe também uma relação matemática entre a posição (localização) do objeto P, da imagem P’ e a distância focal f para os espelhos esféricos, denominada equação dos pontos conjugados, num referencial conveniente denominado referencial de Gauss, com as seguintes características
O eixo das abscissas coincide com o eixo principal do espelho.
O eixo das ordenadas coincide com o espelho.
A origem coincide com o vértice do espelho.
Equação dos pontos conjugados ou equação de Gauss para espelhos esféricos
Equação do aumento linear transversal
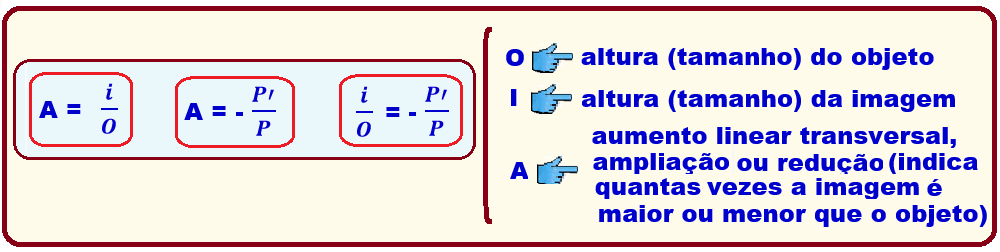
Convenções do referencial de Gauss
No referencial de Gauss adotado no estudo dessas equações, as posições são transformadas em coordenadas onde:
No vértice V do espelho está localizada a origem das abscissas e das ordenadas.
No lado onde a luz incide as abscissas (P e P’) são positivas e no lado oposto, negativas.
As coordenadas (i e O) são positivas acima do vértice do espelho e negativas abaixo.
Imagem real 
P’ > 0, (positivo) imagem virtual, P’< 0 (negativo).
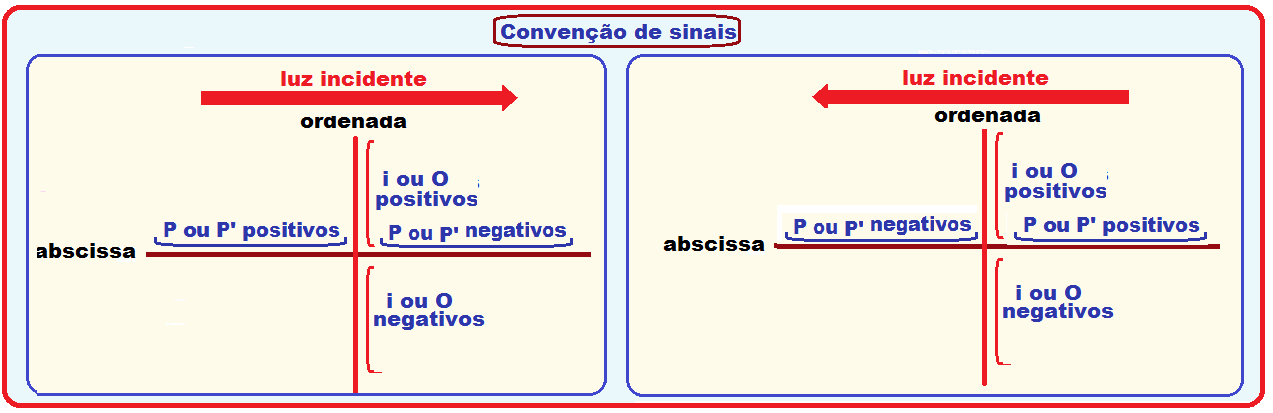
Informações importantes
O que você deve saber, informações e dicas
Toda imagem real pode ser projetada e é invertida (i e o tem sinais opostos) P’ é positivo e i é negativo
Toda imagem virtual é direita P’ é negativo e i é positivo
Demonstração da equação dos pontos conjugados ou equação de Gauss
Para a demonstração da equação de Gauss, vamos considerar um objeto de altura O e sua correspondente imagem de altura i conjugada por um espelho esférico côncavo, conforme a figura abaixo.
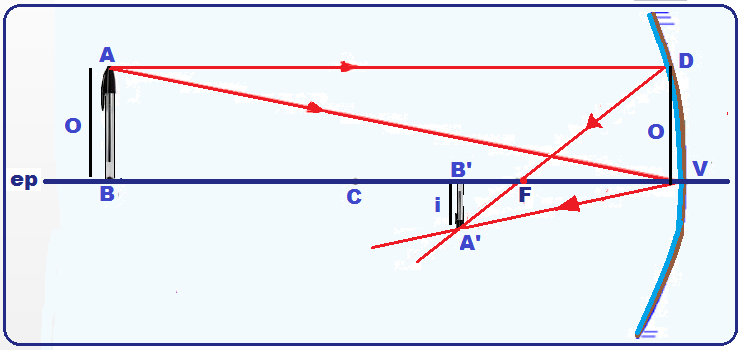
Os triângulos ABV e A’B’V são semelhantes
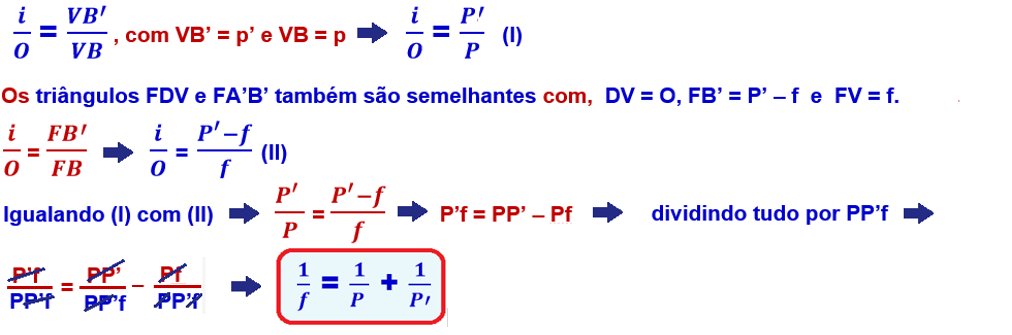
Algumas vezes você precisa aplicar a equação dos pontos conjugados mais que uma vez como no exemplo a seguir:
Um objeto desloca-se ao longo do eixo principal, em direção ao vértice de um espelho esférico côncavo Gaussiano, com velocidade constante de 4cm/s. A distância focal do espelho é de 10cm.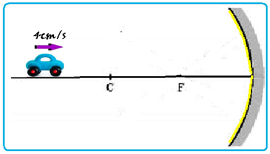
Em um certo instante, o objeto está a 50cm do vértice.
Determine, após 5s, a distância percorrida pela imagem do objeto.
Situação inicial (t = 0) P = 50cm f = 10cm 1/f = 1/P + 1/P’ 1/10 = 1/50 + 1/P’ 1/10 – 1/50 = 1/P’ 4/50 = 1/P’ P’ = 12,5cm (posição inicial da imagem).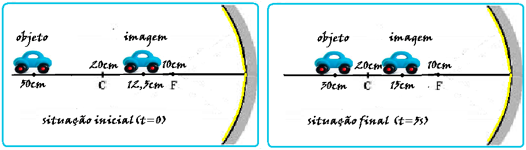
Situação final (t = 5s) V=ΔS/Δt 4= ΔS/5 ΔS=20cm como ele se aproxima do espelho sua nova distância do vértice do espelho será P = 50 – 20 P = 30cm f = 10cm 1/10 = 1/30 + 1/P’ P’= 15cm (nova posição da imagem).
A imagem percorreu ΔS = 15 – 12,5 ΔS = 2,5cm.
Exercício interessante:
A imagem do Sol é formada em um espelho esférico côncavo, de distância focal igual a 1 metro. Considerando a distância do Sol à Terra 250 vezes maior que o diâmetro do Sol, determine o diâmetro da imagem formada.
Sendo a distância do Sol à Terra muito grande, os raios de luz emitidos por ele chegam à Terra como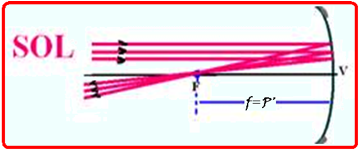
feixes de raios paralelos e a imagem P’ do Sol se forma no foco P’ = f = 1m P=250d O = d i/O = – P’/P i/d = – 1/250d i = -1/250 = 4.10-3m (i < 0, imagem do Sol invertida e de diâmetro
0,004 m)
Comparando as distâncias aparentes entre um espelho esférico convexo e um espelho plano
Para evitar acidentes de trânsito, foram instalados espelhos convexos em alguns cruzamentos.
A experiência não foi bem sucedida porque, como os espelhos convexos fornecem imagens menores, perde-se completamente a noção de distância. 
Para perceber esse efeito, suponha que um objeto linear seja colocado a 30 m de um espelho convexo de 12 m de raio, perpendicularmente a seu eixo principal.
a) A que distância do espelho convexo seria vista a imagem desse objeto?
b) Se substituíssemos o espelho convexo por um espelho plano, a que distância deste espelho seria vista a imagem daquele objeto?
a) Objeto a P=30m do espelho convexo de distância focal f = – 6m 1/f = 1/P + 1/P’ -1/6 = 1/30 + 1/P’ P’ = – 5m (observe que para um objeto a 30m do espelho convexo, a imagem seria vista como se estivesse a 5m do mesmo, aparentando assim, ser menor).
b) No espelho plano a imagem é simétrica (objeto e imagem são equidistantes do espelho) e de mesmo tamanho do objeto. Assim você veria a distância real que é de 30m.