Estudo Analítico das Lentes Esféricas – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Estudo Analítico das Lentes Esféricas
01- a) Lente convergente – lentes de vidro no ar, de bordas finas são convergentes ou, observe que , após se refratarem na lente os raios de luz convergem para o eixo principal.
b) P=15cm — P’=10cm — 1/f=1/P + 1/P’ — 1/f=1/15 + 1/10 — 1/f=(10 + 15)/150 — f=150/25 — f=6cm
02- a) largura do quadro da fita=tamanho do objeto — o=35mm — o=35.10-3m — largura da tela=tamanho da imagem —
i= – 10,5m ( negativo, pois toda imagem real “projetada” é invertida) — P’=30m — A=i/o= – 10,5/35.10-3 — A= – 300 (a imagem é 300 vezes maior que o objeto e é invertida)
b) A=-P’P/P — -300=-30/P — P=10cm (a fita está a 10cm da lente)
c) 1/f=1/P + 1/P’ — 1/f=1/10 + 1/30 — 1/f=(3 + 1)/30 — f=7,5cm
03- a) A lente é convergente, pois a imagem é projetada (real e invertida) e, na tela ela aprece como direita, pois o slide é colocado invertido — f=5cm — P=6cm — 1/f=1/P + 1/P’ — 1/5=1/6 + 1/P’ — 1/5 – 1/6=1/P’ — 1/P’=(6 – 5)/30 — P’=30cm
b) A=-P’/P=-30/6 — A= -5 (a imagem é ampliada 5 vezes e é invertida)
04- a) 1/50=1/P + 1/52 — 1/50 – 1/52=1/P — 1/P=(52 – 50)/2600 — P=1.300mm=1,3m
b) i= -36mm (negativa, pois é invertida) — i/o=-P’/P — -36/o=-52/1.300 — o=900mm=90cm
05- Na água — f=65cm — P=40cm — 1/65=1/40 + 1/P’ — 1/P’=(40 – 65)/2.600 — P’= – 104cm (negativa, imagem virtual) — i/o=-P’/P — i/0=-(-104)/40 — i=2,6.o (a imagem é direita e 2,6 vezes maior que o objeto) — R- A
06- A e b) A lente é convergente porque a imagem é maior que o objeto e porque é projetada e consequentemente real e invertida —
i= – 4.o — i/o=-P’p/P — – 4.o/o = -P’/P — P’=4P — 1/f=1/P + 1/P’ — 1/12=1/P + 1/4P — 1/12=(4 + 1)/4P — 4P=60 —
P=15cm (distância do objeto à lente) — P’=4P — P’=4.15 — P’=60cm (distância da imagem à lente)
07- o=15cm — i=+3cm (positiva porque toda imagem virtual é direita) — P=30cm — i/o=-P’/P — 3/15=- P’/30 — P’= – 6cm — módulo P’=6cm
08- Observe a figura abaixo: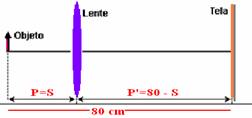
1/15=1/S + 1/(80 – S) — 1/15=(80 – S) + S/S.(80 – S) — 1200=80S – S2 — S2 – 80S + 1200=0 — Δ=B2-4.A.C — Δ=40 —
S= – B ±√ Δ/2.A — S1=(80 + 40)/2 — S1=60cm e P1’=80 – 60=20cm — S2=(80 – 40)/2 — S2=20cm e P2’=80 – 20=60cm
Observe que, para que a imagem seja real e nítida sobre a tela existem duas posições entre elas 20cm e 60cm, mas a distância d
entre essas duas posições é a mesma e vale d=60 – 20 — d=40cm
09- a) o=0,6cm — P=20cm — se objeto e imagem estão do mesmo lado, a imagem é virtual e P’=
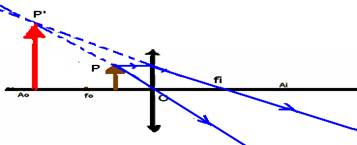
– 100cm — 1/f=1/P + 1/P’ — 1/f=1/25 + 1/-100 — 1/f=3/100 — f=100/3cm, mas a convergência C será em dioptrias se f estiver em metros — C=1/f=1/(1/3) — C=3 di
b) i/o=-P’/P — i/0,6=-(-100)/25 — i=2,4cm
10- a) 1/f=1/180 + 1/36 — 1/f=(1 + 5)/180 — f=30cm
b) O comprimento da imagem da lâmpada é de – 24 cm. A representação geométrica está representada na figura adiante.
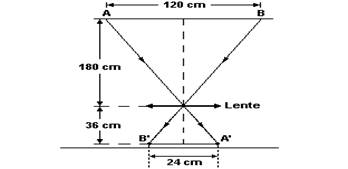
Semelhança de triângulos — 120/A’B’=180/36 — A’B’=24cm
11- Cálculo da altura da imagem formada pela lente L1 — 1/1,5=1/2 + 1/P’ — 1/1,5 – 1/2= 1/P’ — P’=6cm — i/o=-P’/P — i/1=-6/2 — i= – 3cm (negativa, pois é invertida)
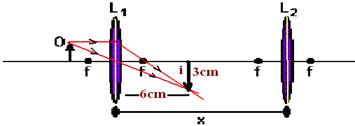
Lente L2 — O=3cm i=-6cm (deve ser direita em relação ao objeto, portanto invertida em relação a i) — i/O=-P’/P — – 6/3=
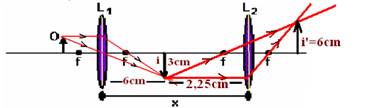
-P’/P — P’=2P — 1/1,5=1/P + 1/2P — P=2,25cm — x=6 + 2,25 — x=8,25cm
12- Lente Lx — f=-10cm (divergente) — P=20cm — 1/-10=1/20 + 1/P’ — -1/10 – 1/20=1/P’ — P’=-20/3cm (virtual, atrás da lente)
Lente Ly — f=10cm — P=20cm — 1/10=1/20 + 1/P’ — 1/10 – 1/20=1/P’ — 1/P’=(2 – 1)/20 — P’=20cm
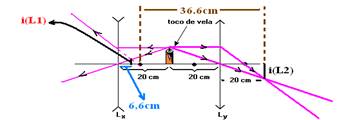
D=60,0 – 6,6 — d=53,4cm — R- E
13- Lente L1 — A’B’ — lente L2 — A’’B’’
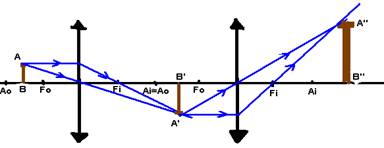
A imagem final é real (intersecção dos próprios raios luminosos), direita e maior em relação ao objeto original.
14- Espelho côncavo — 1/30=1/60 + 1/P’ — 1/30 – 1/60=1/P’ — P’=60cm (A’B’)
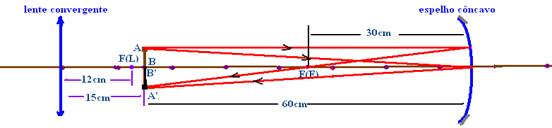
Lente convergente — a imagem i(E) conjugada pelo espelho funciona como objeto para a lente — P=15cm — f=12cm — 1/12=1/15 + 1/P’ — 1/ 12 – 1/15=1/P’ — 1/P’=(5 – 4)/60 — P’=60cm
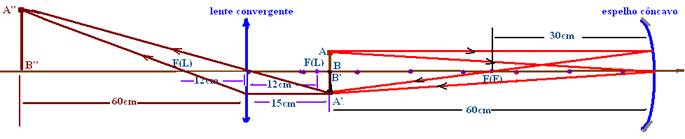
R- A
15- a) Trata-se de uma lente convergente (bordas finas) de índice de refração em relação ao ar – nlente/nar=1,35 — face convexa – Rc=2,5.10-3 m — face plana Rp=∞ — equação dos fabricantes de lentes C=1/f=((nlente/nar – 1).(1/Rc + 1/Rp) — C=1,35 – 1,00).(1/2,5.10-3 +1/∞) — C=(0,35).(0,4.103 + 0) — C=140di
b) Se a imagem é direita — i=50.O — i/O=-P’/P — 50.O/O=-P’/P — P’=-50P — 1/f=140m — 1/f=1/P + 1/P’ — 140=1/P – 1/50P — 140=49/50P — P=0,007m=7mm
16- a) f=20cm — P=60cm — 1/20=1/60 + 1/P’ — 1/20 – 1/60 =1/P’ — 1/P’=(3 – 1)/60 — P’=30cm
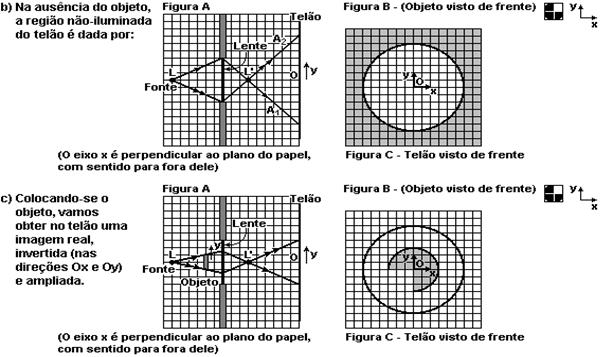
Como a imagem é projetada, ela é invertida (troca cima por baixo) e reversa (troca direita pela esquerda) Figura C)
17- nv=1,5 — nar=1,0 — Rc=2.10-2m — Rp=∞ — equação dos fabricantes de lente — 1/f=C=(nv – nar).(1/Rc + 1/Rp) —
1/f=(1,5 – 1,0).(1/2.10-2 + 0) — 1/f=25m — P’=-36cm=-36.10-2m (negativa-imagem virtual-lente divergente) — 1/f=1/P + 1/P’ — 25=1/P – 1/36.10-2 — 25 + 1/36.10-2=1/P — P=0,04m — i=20.10-2 m (positiva – direita) — i/O=-P’/P —
20.10-2/O=-(-36.10-2)/4.10-2 — O=2.10-2m — O=2cm — R- D
18- 1- Correta – os raios de luz paralelos provenientes do Sol, se refratam na lupa (lente convergente) e convergem para um único ponto que é o foco.
2- Falsa – é direita e virtual
3- Correta – f=20cm — P=10cm — 1/f=1/P + 1/P’ — 1/20 – 1/10 =1/P’ — P’= -20cm — i/o=-P’/P — i/o=-(-20)/10 —
i/o=2 — i=2.o
R- D
19- Uma lente convergente funciona como lupa somente se o objeto estiver entre o foco e a lente — C=1/f — 5=1/f — f=0,2m — f=20cm — R- C
20- Inicialmente o alvo está no foco da lente, pois a imagem é nítida — aproxima-se a vela da lente até P=3f/2 — P’=? — 1/f=1/P + 1/P’ — 1/f=1/1,5f +1/P’ — 1/f – 1/1,5f=1/P’ — 0,5/1,5f=1/P’ — P’=3f — R- E
21- a) Como a imagem está projetada no anteparo, ela é real. O objeto também é real. Concluímos que se trata de uma lente convergente.
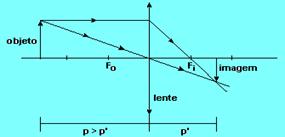
b)
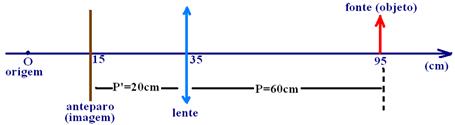
1/f=1/P + 1/P’ — 1/f=1/60 + 1/20 — 1/f= (1 + 3)/60 — f=15cm
22- 1/f=1/08f + 1/P’ — 1/f – 1/08f =1/P’ — (0,8 – 1,0)/0.8f=1/P’ — P’=-4f — i/o=-P’/P — i/1,6=-(-4f)/0,8f — i=8mm
23- Como a imagem é projetada, ela é invertida — A=-20=-P’/P — P’=20P — 1/f=1/P + 1/20P — 1/d=1/P + 1/20P — 20P=21d — P’=20P=21d — R- D
24- a) i=2.o — i/o=-P’/P — 2.o/o=-P’/P — P’=-2P — 1/f=1/P – 1/2P — 1/f=(2 – 1)/2P — f=2P — f/P=2
b) Com água — fa=2,5f — P é o mesmo e vale — P=f/2 — 1/fa=1/P + 1/Pa’ — 1/2.5f=1/(f/2) + 1/Pa’ — 1/2,5f – 2/f=1/Pa’ — 1/Pa’ =(1 – 5)/2,5f — Pa’ = – 0,625f — A= – Pa’/P — A= – (-0,625f)/f/2 — A=1,25
25- Dados — P = 30 cm — f = 10 cm — o = 6 cm.
a) 1/f=1/P + 1/P’ — 1/10=1/30 + 1/P’ — (3 – 1)/30=1/P’ — P’=15cm — essa imagem real (p’ > 0) da vela funciona como objeto real para o espelho plano, que fornece uma segunda imagem, virtual e simétrica conforme você pode observar na figura
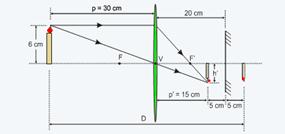
fornecida onde a distância D da imagem final da vela até a mesma vale — D = 30 + 20 + 5 — D = 55 cm.
b) O altura da imagem da vela fornecida pelo espelho plano é igual a altura da imagem fornecida pela lente, pois a imagem formada no espelho plano tem o mesmo tamanho que o objeto — equação do aumento linear transversal — i/o=-P’/P —
i/6=-15/30 — i= – 3cm — a imagem é invertida e tem altura de 3 cm.
26- A figura mostra a construção da imagem: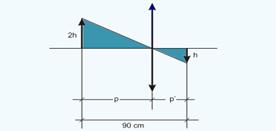
Observe na figura acima que os triângulos sombreados são semelhantes — 2h/h=P/P’ — P=2P’ — P + P’+=90 — 2P’ + P’+=90 — P’=30cm — P=60cm — 1/f=1/P + 1/P’ — 1/f=1/60 + 1/30 — f=60/3 — f=20cm — C=1/f — C=1/0,2 — C=5di
27- Uma lente esférica é delgada quando sua espessura é desprezível, em ralação aos raios de curvatura das faces. Ela pode ser de bordas delgadas (finas) ou de bordas grossas, como representado abaixo.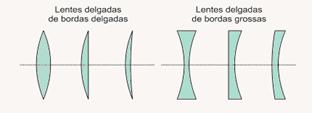
(01) Errada — se o índice de refração do material que constitui a lente é maior que o índice de refração do meio, lentes delgadas de bordas delgadas são convergentes e lentes delgadas de bordas grossas são divergentes.
(02) Correta — trata-se do Teorema da Vergência.
(04) Correta.
(08) Correta.
(16) Correta.
R- (02 + 04 + 08 + 16) = 30
28- a) Falsa — a lente usada para projeções de imagens (de objetos reais) é convergente, e para correção de miopia utiliza-se lente divergente.
b) Falsa — iImagens virtuais não são projetáveis.
c) Correta.
d) Falsa — as faces dos prismas são espelhos planos, fornecendo imagens de mesmo tamanho.
e) Falsa — A lupa fornece imagem virtual, não podendo ser projetada.
R- C
29- Dados — y = 4 cm — y’ = 1 cm — p = d = 3 cm — p’ = D = 150 cm — T = 250 °C — calculando o aumento linear transversal (em módulo), antes do aquecimento.
![]()
Depois do aquecimento, o aumento linear é o mesmo, pois não se alteram as posições do objeto e da imagem — os novos comprimentos da imagem e do objeto são, respectivamente: (y’ + ∆y’) e (y + ∆y) — aplicando novamente a equação do aumento — A=(Y’+ ∆Y)/(Y + ∆Y) — substituindo valores — 50=(200 + 1)/(4 + ∆Y) — ∆y=2.10-2cm — ∆y é a dilatação sofrida pelo objeto — ∆y=Yα ∆T — 2.10-2=4α250 — α=2,0.10-5 oC-1
30-Determinação gráfica da imagem — LM – objeto — L’M’ – imagem:
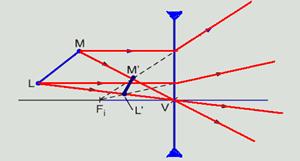
A figura abaixo mostra as coordenadas X e Y dos pontos M e L — M(25;15) — L(5;35):
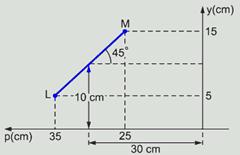
Cálculo da coordenada P’ das imagens M’ e L’ pela equação dos pontos conjugados — 1/f=1/PM + 1/P’M — 1/-20=1/25 + 1/P’M — P’M= – 100/9cm — 1/f=1/PL + 1/P’L — 1/-20=1/35 + 1/P’L — P’L= – 140/11cm — cálculo da coordenada Y’ das imagens M’ e L’ pela equação do aumento linear transversal — Y’L/YL= – P’L/PL — Y’L/5= – ( – 140/11)/35 — Y’L=20/11cm —
Y’M/YM= – P’M/PM — Y’M/15= – ( – 100/9)/25 — Y’M=20/3cm — Comprimento da imagem da barra — c2= (P’M – P’L)2 + (Y’M – Y’L)2 — c2={ – 100/9 – ( – 140/11)}2 + (20/3 – 20/11)2 — c2≈256.000/9.800 — c2≈26 — c≈5,1cm
31- I. Falsa — a moeda não está na posição vista aparentemente devido ao fenômeno da refração, que desvia os raios luminosos.
II. Correta — você pode acender o palito de fósforo colocando a cabeça dele no foco, ponto de encontro dos raios solares refratados pela lente convergente.
III. Correta.
IV. Correta — o número de imagens (n) fornecidas pela associação de dois espelhos planos é dado por:
N=360/θ – 1, sendo θ o ângulo formado entre os espelhos — se os espelhos são colocados paralelamente entre si, θ= 0º — então n tende para infinito.
R- E
32- Observe na figura abaixo que P=7,5cm — f=+5cm — 1/f=1/P + 1/P’ — 1/5=1/7,5 + 1/P’ — P’=37,5/2,5 — P’=15cm —
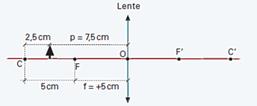
P’ > 0 — imagem real — aumento linear transversal — A= – P’/P= – 15/7,5 — A= – 2 — como A < 0 a imagem é invertida e como │A│=2, a altura da imagem é o dobro da altura do objeto — observe a construção geométrica abaixo:
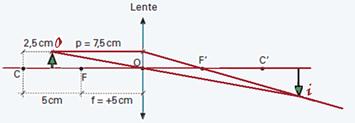
33- Lente convergente — f=+4cm — a imagem é direita (aumento positivo) e de tamanho três vezes maior que o do objeto —
A=+3
a) A= – P’/P — 3= – P’/P — P’= – 3P — 1/f=1/P + 1/P’ — 1/4 = 1/P – 1/3P — 1/4 = 2/3P — P=8/3 cm (distância do objeto à lente)
b) P’ = – 3P — P’= – 3.(8/3) — P’= – 8 cm — como a imagem é virtual, ela é direita e se encontra a 8cm do centro óptico da lente, e do mesmo lado que o objeto — imagem direita — A > 0 — A= i/o — 3=i/0,7 — i=+2,1cm (tamanho da imagem)
— observe a construção geométrica da imagem na figura abaixo:
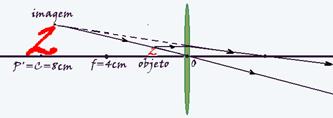
34- R- (01 + 04 + 16)=21 — veja teoria
35- Observe na figura abaixo — o=altura do objeto=1cm — i=altura da imagem= – 0,4cm (invertida em relação ao
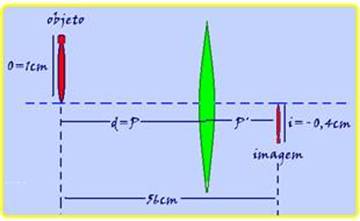
objeto) — distância do objeto à lente=P=d — distância da imagem à lente=P’ — P + P’ = 56cm — P=56 – P’ — i/o = – P’/P — – 0,4/1 = – P’/(56 – P’) — 0,4.56 – 0,4P’=P’ — 1,4P’=22,4 — P’=16cm — P + P’=56 — P + 16=56 — P=d=40cm.
36- Lupa – Também chamada de lente de aumento é uma simples lente convergente que fornece de um objeto colocado entre seu foco F e seu centro óptico O uma imagem virtual, direita e maior que o objeto observado — Observe no esquema abaixo a


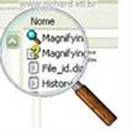
formação da imagem A’B’ de um objeto AB em uma lupa — observe que a imagem é virtual e assim, nas equações — 1/f =
1/P + 1/P’ — i/o = -P’/P — A = i/o = -P’/P — P’ deve e ser substituída com sinal negativo, pois P’< 0 (a imagem é virtual) — dados do exercício — f=+10cm (lente convergente) — i=+100 (toda imagem virtual é direita) — i/o = – P’/P — 100.o/o = – P’/P — P’ = – 10P — equação dos pontos conjugados de Gauss — 1/f=1/P + 1/P’ — 1/10=1/P + 1/(- 10P) — 1/10=1/P – 1/10P —
P=10 – 1 — P = 9cm (distância entre a lupa e o objeto que é a impressão digital) — R- A
37- Como os raios de luz incidem paralelamente na superfície da lupa (lente convergente), eles se refratam convergindo para o foco f formando o ponto luminoso — f=20cm — o celular é o objeto que está a 15cm da lupa — P=15cm — 1/20 = 1/15 + 1/P’ — (3 – 4)/60=1/P’ — P’= -60cm (imagem virtual P’<0) — i/o= – P’/P — i/o= – (-60)/15 — i/o=4 — A=4 — imagem direita (A>0) e 4 vezes maior que o objeto — R- C — observação — como o objeto está entre o foco e a lente convergente
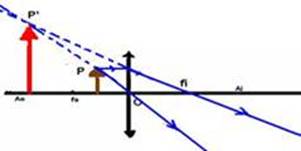
(lupa), você poderia traçar os raios de luz e caracterizar a imagem obtida — natureza: virtual (obtida no cruzamento dos prolongamentos dos raios luminosos) — localização: antes do foco — tamanho e orientação: maior que o objeto e direita em relação a ele.
38- Observando o gráfico fornecido você notará que, quando o objeto estiver a 20cm do centro óptico da lente (P=20cm), a imagem estará também a 20cm do centro óptico da lente (P’=20cm) — essas duas posições correspondem aos dois pontos antiprincipais da lente, que correspondem ao dobro da distância focal — 2f=20 — f=10cm — analisando cada alternativa:
I. Falsa — a vergência C de uma lente corresponde ao inverso de sua distância focal, medida em metros — C=1/f=1/0,1 — C=10 dioptrias (di)
II. Falsa — quando o objeto estiver entre 0 e 10cm do centro óptico da lente, ele estará entre o foco e a lente e a imagem
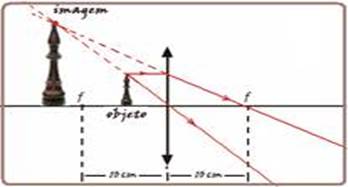
conjugada será virtual, direita e maior em relação ao objeto, como você pode observar na figura acima.
III. Verdadeira — dados — P=50cm — f=10cm — P’=? — equação dos pontos conjugados — 1/f = 1/P + 1/P’ —
1/10 = 1/50 + 1/P’ — 1/p’ = 4/50 — p’ = 12,5cm — aumento linear transversal — A= – P’/P= – 12,5/50 — A= – 1/4 ( o
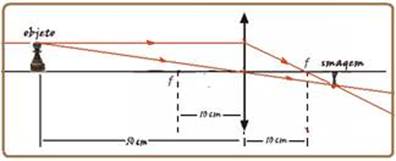
sinal negativo mostra que a imagem é invertida em relação ao objeto — veja figura acima — R- B
