Dioptro Plano

Dioptro Plano

Um dioptro plano é um sistema refrator que apresenta dois meios transparentes e homogêneos separados por uma superfície ou, mais especificamente consiste num conjunto de dois meios opticamente homogêneos e transparentes separados por uma superfície plana como, por exemplo,

o ar em contato com a água parada e transparente de uma piscina (dioptro plano “ar-água”)

Localização das imagens num dioptro plano

Quando observamos uma pessoa mergulhada numa piscina cheia de água, estamos observando sua imagem virtual, que está acima do objeto.

Da mesma maneira, se estivermos debaixo da água, e olharmos para um corpo fora da piscina, estaremos observando sua imagem virtual, que está acima do objeto.

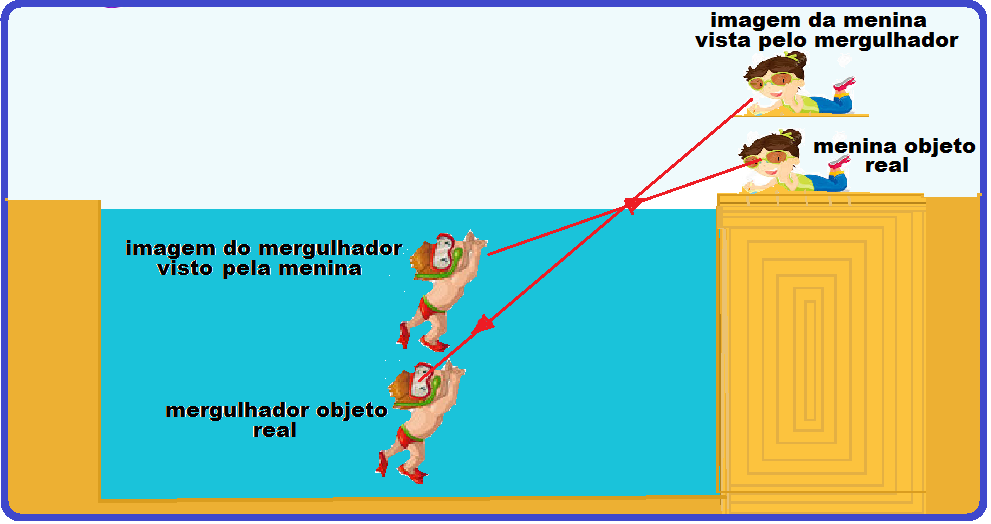
Essa posição, diferente da real, em que enxergamos a imagem virtual, chamamos de posição (ou distância) aparente.

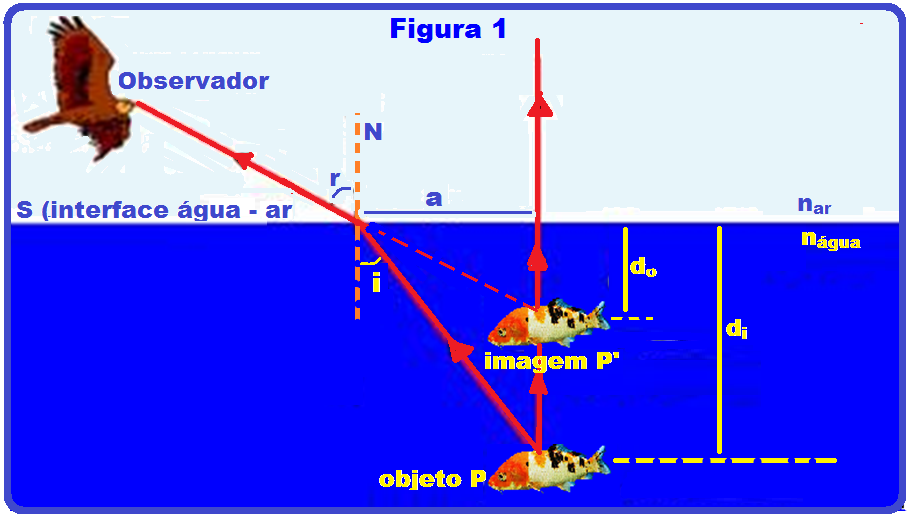
Na figura 1 o ponto objeto real P está dentro da água (mais refringente, maior índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao se refratar para o ar, afasta-se da normal atingindo os olhos do observador e determina a imagem virtual (P’), obtida no prolongamento desse raio e onde ele intercepta o raio de luz vertical, fornecendo essa imagem P’, acima do objeto real P.

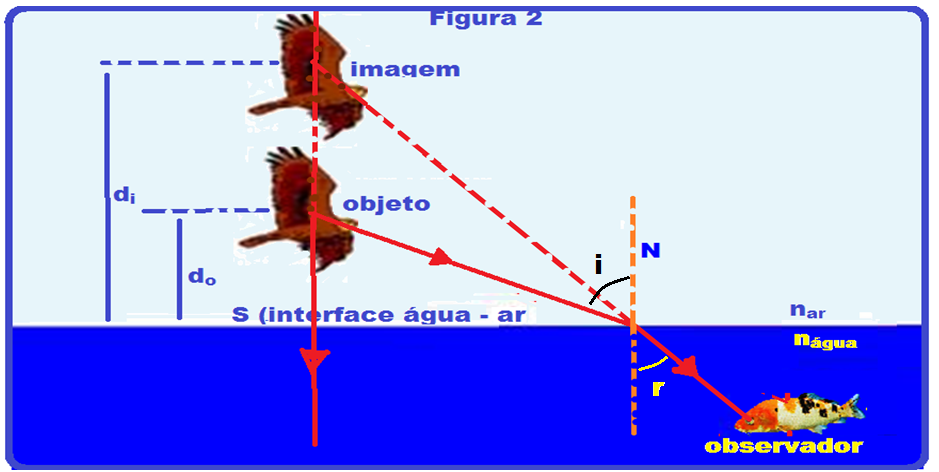
 Na figura II o ponto objeto real P está no ar (menos refringente, menor índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao refratar-se para  a água aproxima-se da normal atingindo os olhos do observador e determina a imagem virtual P’, acima do objeto real P.

Observe que, em ambos os casos a imagem está sempre acima do objeto.

Dedução da equação do dioptro plano

Aplicando a lei de Snell-Descartes, por exemplo, no primeiro caso acima, temos:

n_1.seni = n₂senr (I)   considerando os ângulos muito pequenos de modo que o observador esteja bem próximo da normal de maneira que o seno e a tangente de cada ângulo sejam aproximadamente iguais ou seja, seni ≈ tgi  ≈ a/d_o  (II)  e  senr ≈ tgr ≈ a/d_i    (III).

Substituindo (II) e (III) em (I)  n_1.d_o = n_2.d_i.

Como utilizar a equação do dioptro-plano

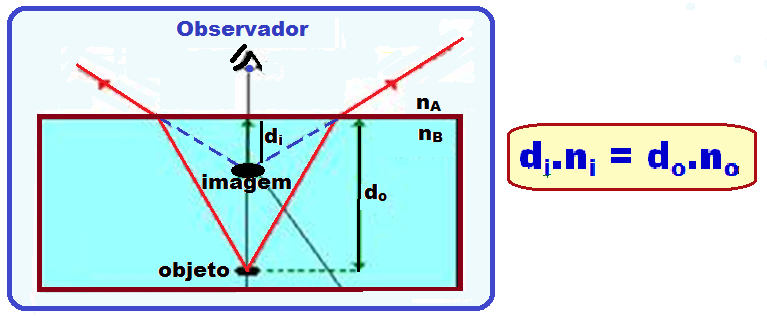
Sendo:

d_i distância vertical da imagem à superfície de separação dos meios A e B (distância aparente, em que o observador enxerga a imagem)

d_o distância vertical do objeto, até a superfície de separação dos meios A e B.

n_o índice de refração do meio onde está o observador (no caso, meio A)

n_i índice de refração do meio onde está o objeto e a imagem (no caso, meio B)

Um exemplo de aplicação: 

De acordo com o desenho, onde você tem um peixe e uma andorinha se visualizando mutuamente. Considerando o índice de refração absoluto da água como n_água = 1,3 e o índice de refração absoluto do ar como n_ar = 1,0, pede-se:

 

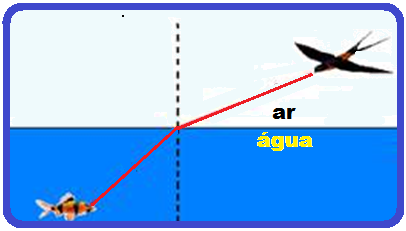
a) Determine a altura aparente com que o peixe verá a andorinha sabendo que ela se encontra a 10m da superfície livre da água.

n_o   índice de refração do meio onde está o observador, no caso, o peixe n_o = n_água = 1,3. n_i índice de refração do meio onde está o objeto e a imagem, no caso, o ar n_i =n_ar = 1,0.

d_o distância vertical do objeto (andorinha), até a superfície de separação d_o = 10 m.

d_i distância vertical da imagem da andorinha até a superfície de separação d_i = ?

d_i.n_i = d_o.n_o d_i.1,0 = 10.1,3 d_i = 13 m (altura aparente da andorinha) altura de sua imagem vista pelo peixe em relação à superfície da água.

b) Determine a profundidade aparente com que a andorinha verá o peixe sabendo que ele se encontra a uma profundidade de 2,6 m da superfície livre da água.

n_o   índice de refração do meio onde está o observador, no caso, a andorinha n_o = n_ar = 1,0.

n_i índice de refração do meio onde está o objeto e a imagem, no caso, a água n_i = n_água = 1,3.

d_o distância vertical do objeto (peixe), até a superfície de separação d_o = 2.6 m.

d_i distância vertical da imagem do peixe até a superfície de separação d_i = ?

d_i.n_i = d_o.n_o d_i.1,3 = 2,6.1,0 d_i = 2,6/1,3 d_i = 2,0 m (profundidade aparente do peixe em relação à superfície) altura aparente do peixe visto pela andorinha.

O que você deve saber, informações e dicas

 Em qualquer situação a imagem está sempre acima do objeto e ambos na mesma reta vertical.

A posição da imagem depende do ponto de onde o observador estiver olhando.

Se ele estiver numa direção

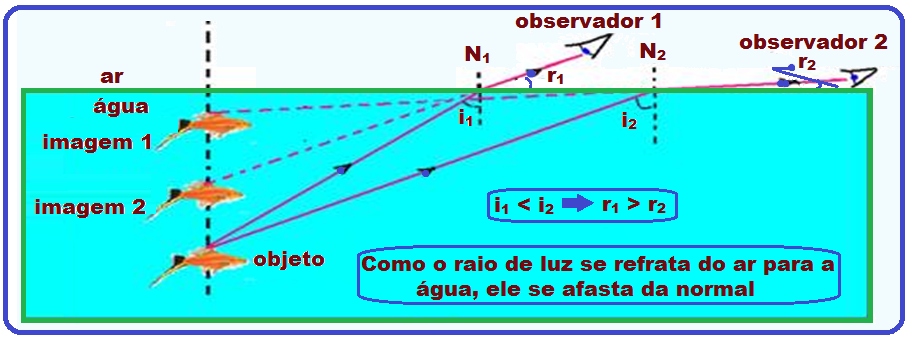
 aproximadamente perpendicular à superfície da água, a expressão d_i.n_i = d_o.n_o é sempre válida.

À medida que ele se afasta, a imagem vai parecendo cada vez mais elevada.

Um gato que observa um peixe dentro de um aquário enxerga-o mais próximo da parede do aquário (observador no ar).

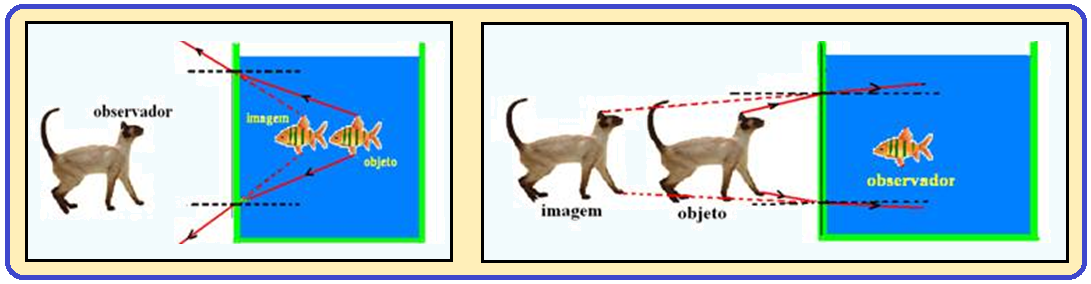
Ao mesmo tempo, o peixe observa o gato mais distante do aquário (observador na água).

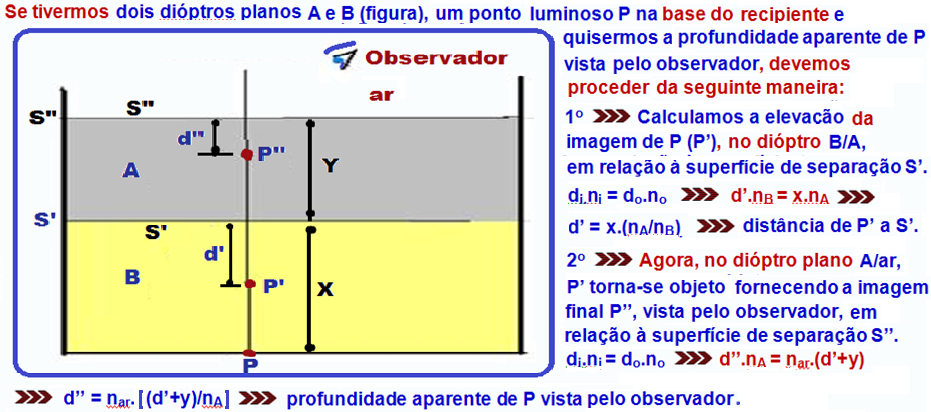
 Se você quiser pode resolver o exercício de número 10 com a respectiva resolução, que é sobre esse assunto.

 

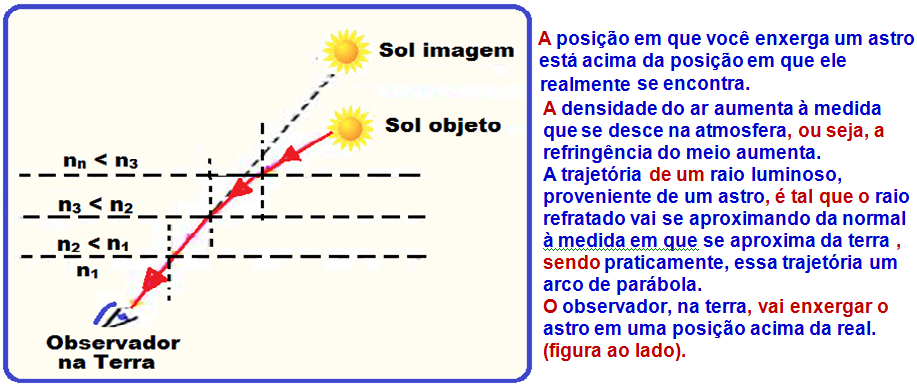
Exercício interessante:

 

Confira os exercícios com resoluções comentadas