Reflexão e Refração de Ondas – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Reflexão e Refração de Ondas
O1- D
02- D
03- Observe nas figuras que, antes da reflexão, a parte da frente da onda (que está em x=9), até chegar à parede percorreu S=6m e que, após a reflexão, chegou até x=3, ou seja, percorreu ΔS=12m. Assim,ΔStotal=6 + 12 = 18m.
Δt=1,5s — V=ΔS/Δt — V=18/1,5 — V=12m/s
R- E
04-
a)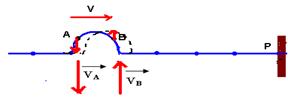
b)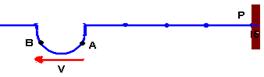
c)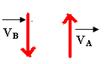
05- B
06- A
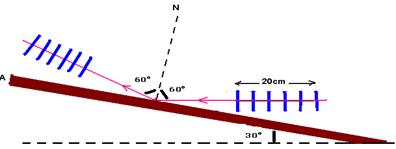
07-Traçando os raios de onda incidente (ri) e refletido (rr), a normal N e lembrando que os ângulos i e r são iguais,, no caso, 45o (figura abaixo).
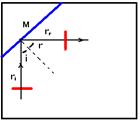
R- A
08- a) V=λ.f — V=6.50 — V=300m/s
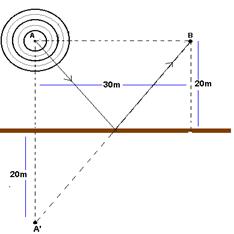
b) tempo (Dt1) que a onda demora para ir de A até B — V=ΔS/Δt1 — 300=30/Δt1 — Dt1 =1/10s a onda refletida se comporta como se fosse emitida em A’, simétrico de A, e a distância (ΔS2) que ela percorre para ir de A’ até B é fornecida aplicando-se o teorema de Pitágoras no triângulo ABA’ — ΔS2=50m.
tempo (Δt2) que a onda refletida demora para ir de A’ até B com velocidade de 300m/s, que é a mesma que das ondas incidentes pois o meio é o mesmo — V=ΔS2/Δt2 — 300=50/Δt2 — Δt2 = 50/300=1/6s
A diferença de tempo de percurso vale Dt=1/6 – 1/10 — Dt=(10-6)/60 — Dt=0,067s
c) As ondas refletidas se comportam como se fossem emitidas pela fonte colocada em A’, simétrico de A.
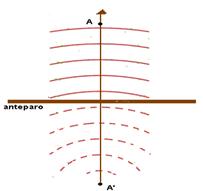
09- R- D A freqüência é a mesma (mesma fonte). A velocidade de propagação é a mesma (mesmo meio). O comprimento de onda é o mesmo. O ângulo de incidência (que o raio de onda forma com a normal no ponto de incidência) é igual ao ângulo de reflexão (que o raio refletido forma com a normal no ponto de incidência)
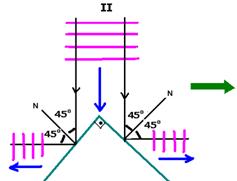
10- Traçando em cada caso, os raios de onda, os ângulos de incidência e de reflexão, teremos:
I-
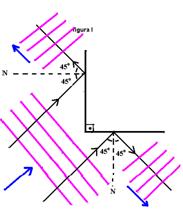
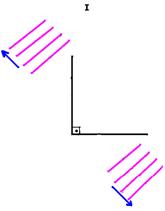
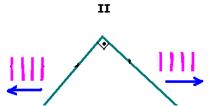
II-
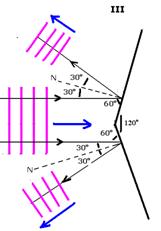
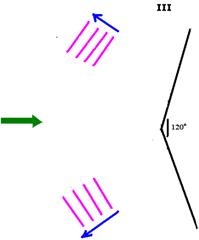
III-
IV-
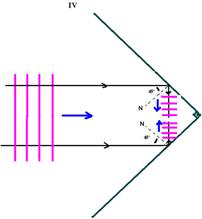
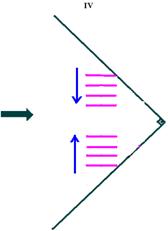
Lembre-se de que as ondas refletidas tem sempre a mesma velocidade de propagação, a mesma freqüência e o mesmo comprimento de onda.
11-a) V=λ.f — V=1.30 — V=30m/s
b) V=30m/s (é a mesma pois o meio é o mesmo)
c) f=30Hz (é a mesma pois a fonte é a mesma)
d) λ=1m (é o mesmo, pois V=λ.f e V e f são os mesmos)
e) As ondas refletidas comportam-se como se estivessem emitidas pela fonte F’, simétrica de F.
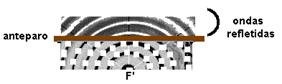
12- a) Cálculo da distância percorrida pela onda em 2s — V=ΔS/Δt — 8=ΔS/2 — ΔS=16cm
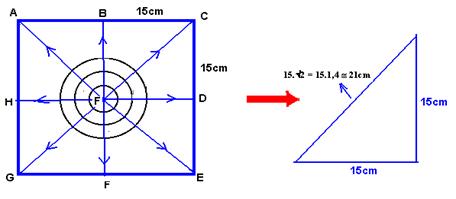
Observe na figura acima que, em t=2s, a onda não chegou aos pontos A,C,E e G e que já está voltando dos pontos B, D, F e H.
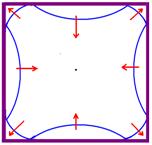
b) Sem inversão de fase, pois as paredes comportam-se como extremidades livres.
13- a) É o mesmo que das ondas incidentes — λ=20/5 — λ=4cm
b) É a mesma que das ondas incidentes, emitidas pela fonte F — V=λf — 10=4f — f=2,5Hz
c)
14- Vamos calcular a distância percorrida por cada ponto da onda no instante t=1,5s — V=ΔS/Δt — 2=ΔS/1,5 — ΔS=3,0m
Verifique na figura abaixo que — AA’=BB’=3,0m e que PP’=QO’=3,0m
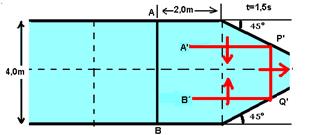
Quando t=1,5s: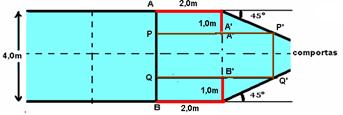
Os pontos da onda entre A’ e P’ já atingiram o anteparo e estão retornando. O mesmo acontece com os pontos da onda entre B’ e Q’.
Os pontos P’ e Q’ estão no anteparo.
Os pontos da onda entre P’ e Q’ ainda não atingiram o anteparo e estão se deslocando para a direita.
15- Meio 1
1,5λ1=6 — λ1=4m V1=λ1.f — 8=4f — f=2Hz
Meio 2
A freqüência f é a mesma, pois a fonte é a mesma — f=2Hz e V2=10m/s — V2=λ2f — 10=λ2.2 — λ2=5m
16- a) λ1=1,5m — V1=λ1f — 12=1,5f — f=8Hz (constante) — V2=λ2f — 8=λ28 — λ2=1m
b) f=8Hz para as duas cordas.
17- a) A razão é 1, pois a freqüência é a mesma em cada corda (mesma fonte)
b) f=4Hz (para as duas cordas) — µ1=4µ2 — T (é a mesma para as duas cordas)
V1=λ1f — f=V1/λ1 V2=λ2f — f=V2/λ2 — V1/λ1=V2/λ2 —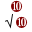 
T/4µ2/λ1)=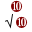T/µ2/λ2) — λ1/λ2=1/2
18- D
19- a)
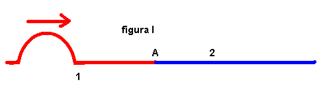
Velocidade do pulso em cada corda V1=18/2=9cm/s — V1=0,09m/s V2=6/2=3cm/s — V2=0,03m/s
Como V1>V2 — µ1 < µ2 e a corda 1 é menos densa “mais leve” que a corda 2. Se o pulso incidente tivesse vindo pela corda 2, mais densa “mais pesada”, o pulso na corda 1 seria sem inversão de fase. Outra explicação: O pulso está na 1 (menos densa), pois ao atingir A (que funciona como extremidade fixa), ele retorna com inversão de fase.
b) Corda 1 — V1=
T/m1 — 0,09=T/0,01 — (0,09)2=(T/0,01)2 — 0,0081=T/0,01 — T =
0,000081N (nas duas cordas)
c) V2=T/m2 — (0,03)2=(0,000081 /m2)2 — 0,0009=0,81//m2 — m2=0,09kg/m
20- D
21– A
22-R: B
Observe na figura abaixo que i=45o e que r=30o
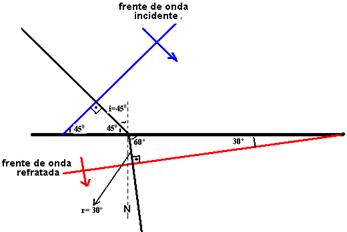
A frequência é a mesma (mesma fonte) — f=10Hz
sen i/sen r = λ1/λ2 — sen 45o / sen 30o = 28/λ2 — 2/2/1/2 = 28/λ2 — λ2 = 20m
23- Freqüência da luz no ar — V=λf — 3.108=633.10-9.f — f ≈ 5.1014Hz
Cálculo do índice de refração do meio — nar.sen60o=nt.sen30o — 1.3 /2=nt.1/2 — nt=3
Velocidade da luz no meio — nt = C/V — 3 = 3.108/V — V = 3.108m/s — V=λf — 3.108 = l.5.1014 — λ ≈ 0,347.10-6 = 347.10-9 = 347 nm
24- a) freqüência no meio 1 — V=lf — 200=4.f — f=50Hz – é a mesma nos dois meios
b) Observe na figura abaixo que i=q1 e que r=q2
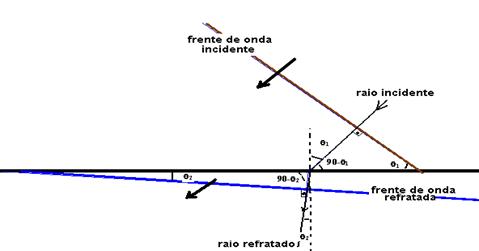
seni/senr = V1/V2 — 0,8/0,5=200/V2 — V2=125m/s
c) V1/V2 = λ1/λ2 — 200/125=4/λ2 — λ2 = 2,5m
d) n2/n1=V1/V2 — n2/n1=200/125 — n2/n1=1,6 — n2=1,6n1
25- D
26- C
27- R – A
I e II- verdadeiras — como a freqüência é a mesma (mesma fonte) — f=V/λ=constante — V e λ são diretamente proporcionais
28- a) A distância entre os máximos sucessivos no meio 1 é o comprimento de onda ΔS = 2,0 cm. Se a onda percorre esta distância em 0,5 s, sua velocidade neste meio será v1= 2,0 / 0,5 = 4,0 cm/s. A freqüência será, portanto, f = V/λ = 4/2=2Hz.
b) Pela Lei de Snell-Descartes, temos
sen30o/sen45o=V1/V2 — 1/2/2/2 = 4/V2 — V2=42cm/s
29-
(01) Falsa. O experimento ilustra o fenômeno da refração.
(02) Correta. A freqüência é a mesma nas duas regiões (mesma fonte).
(04) Falsa. Valem, respectivamente, 2,30cm e 4,00cm (distância entre duas cristas consecutivas)
(08) Verdadeira. Maior comprimento de onda (l), maior velocidade (V).
(16) Verdadeira. V=lf — Como V é a mesma (mesmo meio), l e f são inversamente proporcionais, ou seja, se f aumentar, l tem que diminuir.
Soma (02 + 08 + 16) = 26
30-
(01) Verdadeira. V é diretamente proporcional a l.
(02) Verdadeira. A freqüência é mesma, pois a fonte é a mesma.
(03) Verdadeira. Sempre que ocorre refração, ocorre reflexão.
(04) Falsa. A onda está passando de um meio mais refringente (maior índice de refração) para outro menos refringente (menor índice de refração) e pode haver reflexão total.
(05) Falsa. A velocidade das ondas na superfície dos líquidos depende da profundidade e, para profundidades inferiores a 10m é dada por V=Ögh.
31– a)Observe na figura abaixo que i=30o e r=45o
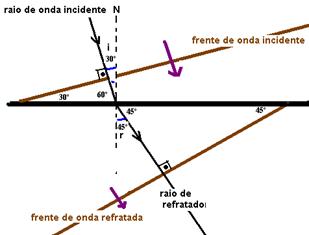
seni/senr = V2/V1 — sen30o/sen45o=340/V2 — 1/2 /2 /2 = 340/V2 — V2 = 3402 m/s
b) Como f é a mesma — V=λf — 3402 = λ2.20 — λ2 = 172 m
32- R: E
Figura 1 — quanto maior o índice de refração n,. maior a freqüência f
Figura 2 — r1 > r3 > r2
Lei — maior n, menor r
Conclusão — maior f, menor
33- nv.senθ1 = nc.senθ2 — 1.√3/2 = nc.1/2 — nc=√3 — nc=c/√3 — nc=c/Vc — √3=3.108/Vc — Vc=√3.108m/s — R- C
34- A frequência f=500Hz é a mesma nos dois meios — Var/λar=Vágua/λágua — λar/λágua = Vágua/Var = 1.500/300=1/5 — R- D
35- ∆S=1cm=10-3m — ∆t=0,1μs=10-1.10-6=10-7s — V=∆S/∆t=10-3/10-7 — V=105m/s — f = 1015.103 = 1018m — V=λ.f — 105=λ.1018 — λ=10-13=10-3.10-10 — λ=10-3 Ǻ — R- B
36- Cada cor possui sua frequência que independe do meio na qual ela está se propagando e, quando a luz passa de um meio
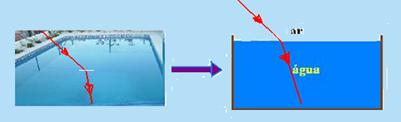
menos refringente para outro mais refringente sua velocidade de propagação diminui — R- E
37- V=λf — f=constante=V/λ — quando a luz passa de um meio mais refringente para um meio menos refringente sua velocidade aumenta e consequentemente seu comprimento de onda também irá aumentar, pois a frequência é a mesma nos dois meios — R-E
38- 1. Falsa — o aquecimento ocorre devido à fricção entre as moléculas de água contidas no alimento, que tendem sempre a se orientar na direção de um campo elétrico de direção variável aplicado pelo magneto.
2. Verdadeira — dados — f = 2.450 MHz = 2,45 109 Hz — considerando a velocidade de propagação das micro-ondas no interior do forno, v = c = 3.108 m/s, da equação fundamental da ondulatória — V=λf — λ=V/f=3.108/2,45.109 — λ=12,2cm
3. Verdadeira — as micro-ondas são refletidas nas paredes para evitar vazamentos, aumentando a segurança do aparelho e a sua eficiência, além de propiciar o aquecimento homogêneo dos alimentos, também favorecido pela rotação do prato.
R- E
39- a) Equação fundamental da ondulatória — Var=λar.f — λar=Var/f=340/160 — λar=2,1m
b) Quando uma onda sofre refração, sua frequência não se altera — far = f = 160 Hz.
c) λágua=Vágua/f=1.450/160 — λágua = 9,1m
40- a) Observe as figuras abaixo — da figura 1 — λar=(18 – 12).10-7m=6.10-7m — equação fundamental da ondulatória — V=λf — c=λar.f — 3.108 = 6.10-7.f — f=5,0.1014Hz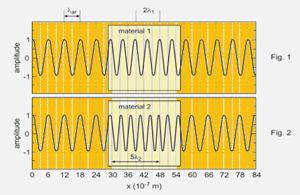
b) Na Fig 1, você observa que, no material 1 — 2λ1 = (48 – 39).10-7 m — λ1=4,5.10-7m — material 2, na figura 2 — 5λ2 = (48 – 30).10-7 m — λ2 =18.10-7/5 — λ2 = 3,6.10-7m — frequência permanece constante nos dois meios, e é também a mesma que a frequência de propagação no ar — f1 = f2 = f = 5.1014 Hz — cálculo da velocidade de propagação da onda em cada meio — v1 = λ1.f = (4,5.10-7)x(5.1014) = 2,25.1088 m/s — v2 = λ2.f = (3,6.10-7)x(5.1014) = 1,8.108 m/s — da definição de índice de refração — n1=c/V1=3.108/2,25.108 — n1=1,3 — n2=c/V2=3.108/1,8.108 — n2=1,7
41- A frequência é característica da onda, sendo sempre a mesma independente do meio — quando a onda sofre refração passando a se mover em meios diferentes, sua velocidade varia e, consequentemente o comprimento de onda também varia — se f1=f2 —
V1/λ1= V2/λ2 — como o comprimento de onda aumentou λ2/λ1>1 — V2/V1>1 — V2>V1 — assi, o meio 2 é menos refringente que o meio 1 — R- D
42-(UEM-PR)
Todas as respostas estão baseadas nas informações abaixo — leia-as atentamente e responda.
Corretas: 01, 04 e 08 — Soma=13.
43-
I. Correta — reverberação é um fenômeno de prolongamento de um som após o fim de emissão por parte de uma mesma fonte sonora — quando o obstáculo refletor do som está um pouco mais afastado, de modo que a som emitido e o som refletido têm um intervalo de tempo menor que 0,1s ocorre o fenômeno da reverberação — nesse caso ao receber dois estímulos do mesmo tipo em menos de 0,1s o ouvinte tem a sensação que o som ainda não foi extinto.
II. Falsa — veja justificativa da I.
III. Correta — eco é uma reflexão de som que chega ao ouvinte pouco tempo depois do som direto — um eco verdadeiro é uma única reflexão do som emitido pela fonte, que você ouve instantes após ouvir o som idêntico inicial.
R- D
44- Equação fundamental da ondulatória — v=λ.f — na água — 1480=2.f — f=740Hz — R- C