Interferência de Ondas – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Interferência de Ondas
01- R: E. Como o pulso A retornará invertido (extremidade fixa) ao se superpuserem os dois pulsos sofrerão interferência destrutiva e em seguida, cada pulso seguirá se caminho mantendo suas características originais
02- Nulas; pois no instante da interferência destrutiva não há movimento dos pontos participantes.
03- B
04- (01+02+04) = 07
05- R- C
06- R – D
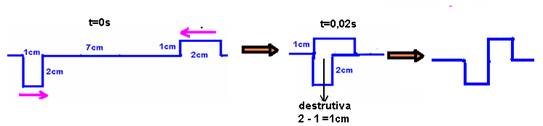
V=ΔS/Δt — 200=ΔS/0,02 — ΔS=4cm
07-
a) A=2m; l=4m e f=0,5Hz — V=lf — 2=4f — f=0,5Hz
b) Após 4s as ondas se deslocaram de V=ΔS/Δt — 2=ΔS/4 — ΔS=8m. Assim, a primeira onda que está voltando invertida e a segunda que está chegando, no instante 4s, se interferem construtivamente e a amplitude da onda resultante será de 2+2=4m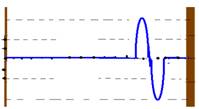
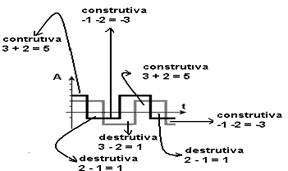
08- Todos os pontos estão em interferência construtiva cuja soma será a altura do retângulo. R: E
09- a) Os pontos A (7m) e B (9m) estão no pulso I que se move para a direita e localizados conforme a figura e suas velocidades verticais indicadas na mesma.
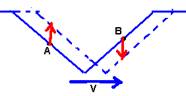
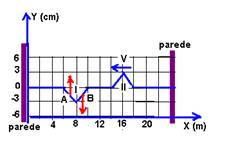
b) Enquanto o pulso I se desloca de 2m na direção X com velocidade de 4m/s, os pontos da corda deslocam-se de 3cm na direção Y, no mesmo intervalo de tempo Δt.
Pulso I — VI=ΔX/Δt — Δt=ΔX/VI — Δt=2/4 — Δt=0,5s
Nesse mesmo intervalo de tempo Δt=0.5s, o ponto A, com velocidade VA, percorreu ΔY=0,03m na direção vertical — VA=ΔY/Δt — VA=0,03/0,5 — VA=0,06m/s ou 6cm/s.
c) Tanto o pulso I como o II, com velocidade de 4m/s, em 1s, deslocam-se, na direção Xde: V=ΔX/Δt — 4=ΔX/1 — ΔX=4m
Como cada pulso desloca-se 4m em sentidos contrários, no instante t=1s eles estarão exatamente
superpostos e ocorrerá interferência destrutiva, com a corda exatamente na horizontal e com todos seus pontos tendo velocidade nula, inclusive C e D.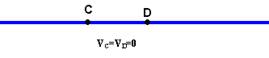
10- A parte da frente de onda da direita (esquema1) percorreu 2cm até atingir o anteparo e mais 3cm de retorno (esquema 2) no intervalo de tempo Δt. A mesma distância percorreu a outra onda.
V=ΔS/Δt — 2=5/Δt — Δt = 2,5s
11- C
12- Veja a figura abaixo:
d1 – d2 = (5λ + X) – X = 5λ = 10.λ/2 — portanto n é par — interferência construtiva de amplitude 2 A
13- B
14- a) Como as duas fontes emitem ondas de mesma freqüência e estão lado a lado, estas ondas estão em fase e José Guilherme ouve esses sons com reforço (interferência construtiva). Mas, com o deslocamento de uma delas a interferência vai ficando destrutiva.
b) V=λf — 340=l680 — λ=0,5m.
A primeira interferência destrutiva ocorre quando n=0. Assim, d=(2n+1).λ/2 — d=(2.0 +1).0,5/2 —-d=0,25m=25cm
15- Como é mínimo, trata-se de interferência destrutiva e é válida a relação d2 – d1 = (2n+1).λ/2, com n=0 (primeiro mínimo).
Observe na figura abaixo que d1=3m e d2=5m

Cálculo do comprimento de onda λ — d2 – d1=5-3=2m — d2 – d1 = (2n+1).λ/2 — 2=(2.0 + 1).λ/2 — λ=4m.
V=λf — 340=4f — f=85Hz
16- E
A interferência é destrutiva, pois o sinal captado é mais fraco. d(FAP)=4m — d(FBP)=5m — d(FBP) – d(FAP)= (2n+1).λ/2 5-4=(2.0 +1).λ/2 — 1=λ/2 — λ=2m
17- E
Observe que o ponto P está exatamente no meio das duas fontes de onda e, então como elas se movem com a mesma velocidade (mesmo meio), haverá sempre uma interferência construtiva, pois as ondas estão em fase.
Assim, duas cristas e dois vales sempre chegarão juntas ao ponto P e a bóia sobe e desce com amplitude que é o dobro da amplitude de cada fonte, mas com o mesmo período T das fontes originais.
18- Observe na figura abaixo que d1=36m e d2=30m
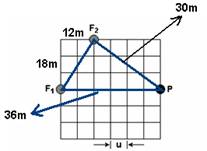
a) Verifique, na expressão da interferência construtiva da onda, onde, d1 – d2 = 2n.λ/2 — λ=d1-d2/n — que λ n são inversamente proporcionais. Assim, o maior comprimento de onda (λ) ocorre quando n=1.
D1 – d2 = 2n.λ/2 — 36-30=2.1.λ/2 — λ=6m
b) Verifique na expressão V=λf — f=V/lλ — que a freqüência (f) e o comprimento de onda (λ) são inversamente proporcionais. Assim:
1a menor freqüência — V=λf —340=6f — f=56,7Hz
2a menor freqüência — d1-d2=2n. λ/2 — 36-30=2.2. λ/2 — λ=3m —- V=λf — 340=3f — f=113,3Hz
19- R – B
V=λf — 340=λ680 — λ=0,5m Interferência destrutiva – X-1,5=(2n+1). λ/2 — mínima (n=0) — X=1,5+ (2.0+1). λ/2 — X=1,75m.
20- O comprimento de onda de cada uma das fontes vale — V=λf — 340=λ.170 — λ=2m
a) Ao atingirem A, as ondas provenientes de F1 e F2 devem sofrer aí, interferência destrutiva (mínimos de intensidade).
Na situação inicial — d(F1A)=10m e d(F2A)=12,5m — d(F2A)- d(F1A)=12,5 -10=2,5m =ΔXi
Na situação de interferência destrutiva com a fonte F2 mais afastada, a distância entre as mesmas será ΔXd
A equação da interferência destrutiva é ΔXd=(2n+1).λ/2. Quando n=0, a solução não satisfaz, pois nesse caso, ΔXd=1m e como F2 deve ser afastada, ΔXd que é a distância entre as fontes, deve ser maior que 2,5m.
Para n=1 — ΔXd=(2n+1).l/2. — ΔXd = (2.1+1).l/2 — ΔXd = (2.1+1).2/2 — ΔXd=3m (La)
b) Ao atingirem B, as ondas provenientes de F1 e F2 devem sofrer aí, interferência construtiva (máximos de intensidade) e, nesse caso, ΔXd=2n.λ/2. A condição n=0 não satisfaz, pois, nesse caso DXd=0 e as fontes estaria coincidentes e sabemos que elas estão distanciadas de mais de 2,5m.
d(F1B)=10m — d(F2B)=?
Para n=1 — ΔXd=2n.l/2 — ΔXd=2.1.2/2 — ΔXd=2m
ΔXd= d(F2B) – d(F1B) — 2= d(F2B) – 10 — d(F2B)=12m
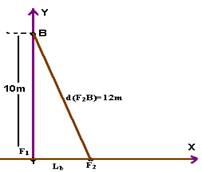
Pitágoras — (10)2 + Lb2=(12)2 — Lb=6,6m
21- R- D — veja teoria
22- a) Não — a interferência é um fenômeno que descreve a soma das amplitudes das onda e, após a mesma, elas continuam seu movimento como se nada tivesse acontecido..
b) Não — a energia de uma onda está relacionada à potência do gerador que a fez oscilar.
23-
Observe a figura abaixo onde está representado o instante em que as ondas estão totalmente sobrepostas — haverá interferência construtiva na metade esquerda do intervalo e destrutiva na metade direita do mesmo intervalo — R- C
24-
01- Como as ondas emitidas pelos dois alto-falantes estão em fase elas possuem a mesma freqüência (f), o mesmo comprimento de onda (λ), e mesma amplitude (A) e em fase (ambas para cima ou ambas para baixo) — nos pontos O e M as ondas estão em concordância de fase (som de intensidade máxima, reforço) — para o ponto M, onde as ondas estão em concordância de fase (interferência construtiva), a distância de uma fonte até M (d2=10m) menos a distância da outra fonte até M (d1=8m), deve valer um comprimento de onda 1λ — d2 – d1=1λ — 10 – 8=1λ — λ=2,0m.
02- Mais próxima — como V=λ.f e como V é constante, o comprimento de onda λ e a frequência f são inversamente proporcionais — assim, como entre O e M existe um λ, se a frequência aumenta, esse λ diminui e o ponto M ficará mais perto do ponto O.
