Exercícios de vestibulares com resoluções comentadas sobre
Interferência de Ondas
01-(UFSCAR-SP) Dois pulsos, A e B, são produzidos em uma corda esticada, que tem uma extremidade fixada em uma parede, conforme mostra a figura.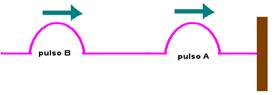
Quando os dois pulsos se superpuserem, após o pulso A ter sofrido reflexão na parede, ocorrerá interferência:
a) construtiva e, em seguida, cada pulso seguirá se caminho mantendo suas características originais.
b) construtiva e, em seguida, os dois pulsos seguirão juntos no sentido do pulso de maior energia.
c) destrutiva e, em seguida os pulsos deixarão de existir, devido a absorção de energia durante a interação.
d) destrutiva e, em seguida, os dois pulsos seguirão juntos no sentido do pulso de maior energia.
e) destrutiva e, em seguida, cada pulso seguirá se caminho mantendo suas características originais.
02-(UFRJ-RJ) A figura 1 retrata, em um dado instante, uma corda na qual se propagam, em sentidos opostos, dois pulsos transversais de mesma forma, um invertido em relação ao outro.
A figura 2 mostra a mesma corda no instante em que a superposição dos pulsos faz com que a corda esteja na horizontal. Estão marcados dois pontos da corda: A e B.
Tendo em conta o eixo transversal orientado representado na figura, cujo sentido positivo é de baixo para cima, verifique se as velocidades escalares dos pontos A e B são positivas, negativas ou nulas. Justifique sua resposta
03-(PUC-PR) O fenômeno da interferência não pode ocorrer com o som, porque, ao contrário da luz, o som consiste de ondas longitudinais. Esta afirmação é:
a) verdadeira, pelos motivos expostos.
b) falsa, pois a interferência se dá nos dois casos.
c) verdadeira, mas não pelos motivos expostos.
d) falsa, pois somente com ondas longitudinais é possível obter interferência.
e) verdadeira, pois em nenhum dos casos, é possível obter interferência.
04-(UFSC) A figura representa dois pulsos de onda, inicialmente separados por 6,0 cm, propagando-se em um meio com velocidades iguais a 2,0 cm/s, em sentidos opostos.
Considerando a situação descrita, assinale a(s) proposição(ões) CORRETA(S):
(01) Inicialmente as amplitudes dos pulsos são idênticas e iguais a 2,0 cm.
(02) Decorridos 8,0 segundos, os pulsos continuarão com a mesma velocidade e forma de onda, independentemente um do outro.
(04) Decorridos 2,0 segundos, haverá sobreposição dos pulsos e a amplitude será nula nesse instante.
(08) Decorridos 2,0 segundos, haverá sobreposição dos pulsos e a amplitude será máxima nesse instante e igual a 2,0 cm.
(16) Quando os pulsos se encontrarem, haverá interferência de um sobre o outro e não mais haverá propagação dos mesmos.
05-(UFC) Duas ondas ocupam a mesma região no espaço e têm amplitudes que variam com o tempo, conforme o gráfico a seguir.
Assinale a alternativa que contém o gráfico resultante da soma dessas duas ondas.
06-(UFSCAR-SP) A figura mostra dois pulsos numa corda tensionada no instante t=0 s, propagando-se com velocidade de 2m/s em sentidos opostos.
A configuração da corda no instante t=20ms é:
07- (UFG-GO) Considere duas ondas que se propagam numa mesma corda homogênea, segundo o esquema abaixo, onde a extremidade da direita é fixa.
As ondas se movem no sentido indicado, a uma velocidade de 2m/s.
a) Qual é a amplitude, o comprimento de onda e a freqüência dessas ondas.
b) Faça o desenho da corda após 4s do instante representado no esquema. Qual é a amplitude da onda resultante?
08- (UNIFENAS-MG) No desenho a seguir, vemos duas ondas se propagarem em uma mesma corda, em sentidos opostos
(figura A).
Quando elas estiverem totalmente superpostas (figura B), a forma da corda será:
09-(FUVEST-SP) A figura representa, no instante t=0 s, a forma de uma corda esticada e presa entre duas paredes fixas, na qual dois pulsos (I e II) se propagam, sem mudar de forma, com velocidade de módulo V=4m/s nos sentidos indicados. Não há dissipação de energia na corda. Considere 4 pontos da corda definidos por suas coordenadas X: A (XA=7,0m), B (XB=9,0m, C (XC=11,0m) e D (XD=13,0m).
a) Indique na figura dada, por meio de setas verticais, os sentidos das velocidades na direção do eixo Y, dos pontos A e B, no instante t=0 s. Se alguma dessas velocidades for nula, escreva “nula”, identificando-a.
b) Determine o valor do módulo da velocidade na direção do eixo Y, do ponto A, no instante t=0 s.
c) Desenhe a forma da corda no instante t=1s. Indique por meio de setas, os sentidos das velocidades na direção do eixo Y, dos pontos C e D. Se alguma dessas velocidades for nula, escreva “nula”, identificando-a.
10-(UEL-PR) Dois pulsos praticamente iguais estão se propagando numa corda elástica AB, com velocidade de propagação de 2cm/s. A extremidade A é livre e nela se originam os pulsos, enquanto a extremidade B é fixa. Considere que a posição dos pulsos no esquema 1 corresponde ao instante t=0.
O esquema 2 também representa a corda elástica AB em outro instante diferente de t=0. Determine o menor intervalo de tempo entre a primeira e a segunda configuração
11-(UFV-MG) Um aparelho de rádio R recebe simultaneamente os sinais direto e refletido em uma camada atmosférica, provenientes de uma emissora E. Quando a camada está a uma altura H, o sinal é forte; à medida que a camada se desloca verticalmente a partir dessa posição, o sinal enfraquece gradualmente, passa por um mínimo e recupera gradativamente o valor inicial.
Esse fenômeno se deve à:
a) difração, pois a facilidade para o sinal contornar a camada é função da altura.
b) variação do índice de refração da camada, que depende de sua altura em relação ao nível da Terra.
c) interferência entre os sinais direto e refletido, construtiva, quando o sinal for máximo, e destrutiva, quando o sinal for mínimo.
d) absorção do sinal pela camada, que depende de sua altura em relação à Terra.
e) variação do índice de reflexão da camada, o qual é uma função da altura.
12-(UFRJ-RJ) Duas fontes, F1 e F2, em fase, produzem ondas periódicas de comprimento de onda λ. A distância entre as fontes vale 5λ. Alinhado com as fontes temos o ponto P, no qual as ondas tem a mesma amplitude A.
13-(UEL-PR) Dois geradores de ondas periódicas situados em pontos P e Q emitem ondas de mesma amplitude e mesmo comprimento de onda. Se as ondas se anulam num ponto M, devido à interferência, a distância MP – MQ, em módulo, pode ser igual a:
14-(UFMG-MG) Em uma loja de instrumentos musicais, dois alto-falantes estão ligados a um mesmo amplificador e este, a um microfone. Inicialmente, esses alto-falantes estão um ao lado do outro, como representado, esquematicamente, nesta figura, vistos de cima
Ana produz, ao microfone, um som com freqüência de 680 Hz e José Guilherme escuta o som produzido pelos alto-falantes. Em seguida, um dos alto-falantes é deslocado, lentamente, de uma distância d, em direção a José Guilherme. Este percebe, então, que a intensidade do som diminui à medida que esse alto-falante é deslocado. Dado que a velocidade do som é de 340m/s.
a) EXPLIQUE por que, na situação descrita, a intensidade do som diminui.
b) DETERMINE o deslocamento d necessário para que José Guilherme ouça o som produzido pelos alto-falantes com intensidade mínima.
15-(UFPE-PE) Duas fontes sonoras pontuais F1 e F2, separadas entre si de 4,0 m, emitem em fase e na mesma freqüência.
Um observador, se afastando lentamente da fonte F1, ao longo do eixo x, detecta o primeiro mínimo de intensidade sonora, devido à interferência das ondas geradas por F1 e F2, na posição x = 3,0 m. Sabendo-se que a velocidade do som é 340 m/s, qual a freqüência das ondas sonoras emitidas, em Hz?
16-(UNIFESP-SP) Duas fontes, FA e FB, separadas por uma distância de 3,0 m, emitem, continuamente e em fase, ondas sonoras com comprimentos de onda iguais. Um detector de som é colocado em um ponto P, a uma distância de 4,0 m da fonte FA, como ilustrado na figura.
Embora o aparelho detector esteja funcionando bem, o sinal sonoro captado por ele em P, é muito mais fraco do que aquele emitido por uma única fonte. Pode-se dizer que
a) há interferência construtiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 5,0 m.
b) há interferência destrutiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 3,0 m.
c) há interferência construtiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 4,0 m.
d) há interferência construtiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 2,0 m.
e) há interferência destrutiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 2m.
17- (FUVEST-SP) Duas hastes, A e B, movendo-se verticalmente, produzem ondas em fase, que se propagam na superfície da água, com mesma freqüência f e período T, conforme a figura 1. No ponto P, ponto médio do segmento AB, uma bóia sente o efeito das duas ondas e se movimenta para cima e para baixo.
O gráfico que poderia representar o deslocamento vertical y da bóia, em relação ao nível médio da água, em função do tempo t, é
18-(UNESP-SP) Duas fontes, F1 e F2, estão emitindo sons de mesma freqüência. Elas estão posicionadas conforme ilustrado na figura, onde se apresenta um reticulado cuja unidade de comprimento é dada por u = 6,0 m.
No ponto P ocorre interferência construtiva entre as ondas e é um ponto onde ocorre um máximo de intensidade. Considerando que a velocidade do som no ar é 340 m/s e que as ondas são emitidas sempre em fase pelas fontes F1 e F2 , calcule
a) o maior comprimento de onda dentre os que interferem construtivamente em P.
b) as duas menores freqüências para as quais ocorre interferência construtiva em P.
19-(UECE-CE) A figura mostra dois alto-falantes A e B separados por uma distância de 2m. Os alto-falantes estão emitindo ondas sonoras em fase e de freqüência 0,68kHz. O ponto P mostrado na figura está a uma distância de 1,5m do alto-falante A.
Supondo que a velocidade de propagação do som no ar seja 340m/s, a distância X mínima do alto-falante B ao ponto P para que este ponto seja um ponto nodal (ponto onde a interferência é destrutiva) é:
a) 1,50m
b) 1,75m
c) 2,00m
d) 2,50m
e) 3,00m
20-(FUVEST-SP) Duas fontes sonoras F1 e F2 estão separadas de 2,5m. Dois observadores A e B estão distantes 10m da fonte F1, sendo que o observador A está no eixo X e o observador B, no eixo Y, conforme figura.
As duas fontes estão em fase e emitem som numa freqüência fixa f=170Hz. Num dado instante a fonte F2 começa a deslocar-se lentamente ao longo do eixo X, afastando-se da fonte F1. Com esse deslocamento, os observadores detectam uma variação periódica na intensidade do som resultante das duas fontes, passando por máximos e mínimos consecutivos de intensidade. Sabe-se que a velocidade do som é de 340m/s nas condições do experimento.Levando em conta a posição inicial das fontes, determine:
a) A separação La entre as fontes para a qual o observador A detecta o primeiro mínimo de intensidade.
b) A separação Lb entre as fontes para a qual o observador B detecta o primeiro máximo de intensidade.
21-(UFMG-MG)
Na Figura I, estão representados os pulsos P e Q, que estão se propagando em uma corda e se aproximam um do outro com velocidades de mesmo módulo.
Na Figura II, está representado o pulso P, em um instante t, posterior, caso ele estivesse se propagando sozinho.
A partir da análise dessas informações, assinale a alternativa em que a forma da corda no instante t está CORRETAMENTE representada.
22-(UEG-GO)
23-(FGV-SP) A figura mostra dois pulsos que se movimentam em sentidos contrários, um em direção ao outro sobre a mesma corda, que pode ser considerada ideal.
No momento em que houver sobreposição total, a disposição esperada para os pontos da corda estará melhor indicada por:
24-(UFMG-MG)
Dois alto-falantes idênticos, bem pequenos, estão ligados ao mesmo amplificador e emitem ondas sonoras em fase, em uma só frequência, com a mesma intensidade, como mostrado nessa figura.
Igor está posicionado no ponto O, equidistante dos dois alto-falantes, e escuta o som com grande intensidade. Ele começa a andar ao longo da linha paralela aos alto-falantes e percebe que o som vai diminuindo de intensidade, passa por um mínimo e, depois, aumenta novamente.
Quando Igor chega ao ponto M, a 1,0 m do ponto O, a intensidade do som alcança, de novo, o valor máximo.
Em seguida, Igor mede a distância entre o ponto M e cada um dos alto-falantes e encontra 8,0 m e 10,0m como indicado na figura.
01- Explique por que, ao longo da linha OM, a intensidade do som varia da forma descrita e CALCULE o comprimento de onda do som emitido pelos alto-falantes.
02- Assinalando com um X a quadrícula apropriada, responda:
Se a frequência emitida pelos alto-falantes aumentar, o ponto M estará mais distante ou mais próximo do ponto O?
Justifique sua resposta.