Resolução comentada dos exercícios de vestibulares sobre Equação da Onda
Resolução comentada dos exercícios de vestibulares sobre
Equação da Onda (Equação fundamental da Ondulatória)
01- B
02-
Falsa – T=1/25 — T=0,04s
Falsa – A=3m
Verdadeira – V=l.f — V=0,2.25 — V=5m/s
Verdadeira
Falsa — l=20cm=0,2m
03- E
04-
F=6/1,5=4Hz — T=1/f=1/4=0,25s
05-
a) 40cm
b)V=
S/t — V=20/0,1 — V=200cm/s=2m/s — V=λ.f — 2=0,4.f — f=5Hz
06- S=0,2m — t=0,008s — V=S/t — V=2.10-1/8.10-3 — V=0,25.102 — V=25m/s
07- a) f=40Hz — T=1/f — T=1/40 — T=0,025=2,5.10-2s
b) V=λ.f — V=15.40 — V=600cm/s=6m/s
08- a) V=λ.f — V=12.30 — V=360m/s (constante-mesmo meio)
O menor λ ocorre quando f=60Hz (vide gráfico) — 360=λ.60 — λmínimo=6m
b) Quando λ=12m, f=30Hz — T=1/f — T=1/30 s
09- V=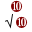
F/
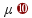— V=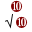64/0,01) — V=
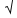6.400 — V= 80 m/s
10-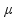 
=m/L — 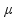=0,01/2 — µ=0,005kg/m — V=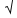200/0,005 — V=200m/s
11- V=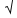F/µ — 40=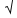24/µ — (40)2 = (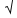24/µ)2 — 1600 = 24/µ — µ = 0,015kg/m
µ =m/L — 0,015 = m/2 — m=0,03kg=3,0.10-2kg
12- µ =10-2kg/m — F=16N — λ=4m — V=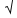F/µ — V=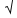16/10-2 — V=4.10 — V=40m/s
V=λ.f — 40=4f — f=10Hz
13- P=mg — 52,9=m.10 — m=5,29kg m=m/L — m=5,29/0,5 — m=10,58kg/m
V=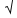F=P/ m — V=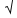52,9/10,58 — V=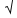5 m/s
14- V=λ.f — 340=3,4.10-3.f — f=105Hz
15- R-A
Da figura — λ=20m Do gráfico — T=10s f=1/T — f=1/10Hz
V=λ.f — V=20.1/10 — V=2,0m/s
16- R: C — Como a freqüência diminui, o período que é seu inverso, aumenta.
17- R: C — No vácuo todas essas radiações eletromagnéticas se propagam com velocidade constante de 3,0.108m/s e V=λ.f
18- V=λ.f — V=2.6 — V=12cm/s — V=DS/Dt — 12=60/Dt — Dt=5s
19- C
λ=150km — V=750km/h — V=λ.f — 750=150f — f=5Hz — T=1/f — T=1/5h — T=1/5.60 — T=12min
20-
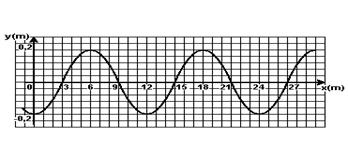
a) Trata-se de uma onda mista, pois oscila na horizontal e na vertical e estas oscilações numa onda mista ocorrem no mesmo tempo nestas duas direções.
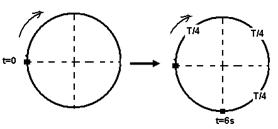
Observe na figura acima, que o intervalo de tempo de 6s corresponde a três quartos do período T, ou seja, T=8s.
b) f=1/T — f=1/8Hz — V=λ.f — 1,5=λ.1/8 — λ=12m
c)
21-
a) O N2 é puro quando a fração molar é zero, ou seja, quando V=350m/s. V=λ.f — 350=λ.800.000 — λ =4,3.10-4m
b) A 60% – V=325m/s — V=S/t — 325=0,1/t — t=0,00307 — t=3,1.10-3 s
22-
a) V=λ.f — 3.108=λ.1.500.106 — λ=2,0.10-1m — porcentagem (fração) nula
b) V=S/t — 3.108=100/t — t = 3,3.10-7 s
23-
a) V=λ.f — 200=150.103.f — f=2/15.10-2Hz — T=1f — T=7,5.102s ou T=750s
b) V=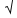g.h — V=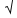10.6,4 — V=8m/s
c) Como V.A2 é constante — V1.A12 na região de formação é igual a V2.A22 na profundidade de 6,4m
200.1=8.A22 — A=5m
24-
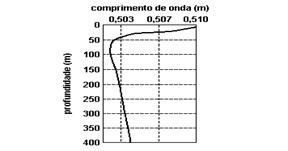
a) De acordo com o gráfico a velocidade mínima ocorre quando V=1505m/s, na profundidade de 75m
b)
25- Observe que, em cada 0,5s, cada crista ou cada vale ou cada ponto da onda percorre 1m
V=S/t — V=1/05 — V=2m/s
26-
a) f =λB — 63.106=42.106.B — B=1,5T Pelo gráfico, quando B=1,5T – x=1.0m
b) V=λf — 3.108=λ.63.106 — λ=0,0476.102 — λ=4,76m
27- B
Mais rasa — V1=2,5.10 — V1=5m/s Mais profunda — V2=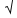10.10 — V2=10m/s
Como f é a mesma — V1=λ1.f — 5=λ1.f — f=5/λ1
V2=λ2.f — 10=λ2.f — f=10/λ2
5/λ1=10/λ2 — λ2=2/λ1
28-
a) No gráfico da figura 1 — T=5s — f=1/T — f=1/5 — f=0,2Hz
b) No gráfico da figura 2 — λ=25m
c) V=λ.f — V=25.0,2 — V=5m/s
d)
29-a) V=λ.f — 3=5f — f=3/5 — f=0,6Hz
b) Não se alteram, pois a amplitude A não está relacionada com V, f el, mas apenas com a quantidade de energia transportada pela onda. Quanto maior a energia, maior a amplitude e vice-versa
30- a) V=λ.f — 2=10.f — f=0,2Hz — T=1/f — T=1/0,2 — T=5s
b) Como se movem em sentido contrário a velocidade relativa entre o barco e a onda é de V=2 + 8 — V=10m/s
V=S/t — 10=10/t — t=1s
31- λ = 12 cm = 0,12 m — c = 300.000 km/s = 3.108 m/s — V=λf — f=V/λ=3.108/0,12 — f=2,5.109 Hz — f=2,5MHz — R- D
32- v = λf — λ=V/f=104/1011=10-7m — λ=100.10-9m=100nm — sendo, pelo enunciado, d=λ — d=100nm —
R- C
33- Observe na figura que entre as duas árvores você observa 4 comprimentos de onda (λ) — 4λ=120 — λ=30m —
V= λf — V=30.0,5 — V=15m/s — R- E
34- A velocidade de propagação é dada pela expressão — 
— 
— movimento uniforme — V=∆S/∆t — 25=10/∆t — ∆t=0,4s — R- B
35- Do painel — menor frequência – f1 = 88 MHz — maior frequência – f2 = 108 MHz — equação fundamental da ondulatória, V = λ f — nessa equação você conclui que, num mesmo meio (mesma velocidade V), o maior comprimento deondacorrespondeà menor frequência e vice-versa — V = λ1 f1 e V = λ2 f2 — igualando-as — λ1 f1 = λ2 f2 — λ1.88 = λ2.108 — λ1/ λ2 = 1,23 — R- E
36- Observando o gráfico você vê que, o período do batimento desse atleta é 0,5 s — T=0,5s — f=1/T=1/0,5 — f=2Hz — portanto, você tem 2 batimentos por segundo ou 2.60=120 batimentos por minuto — R- D
37- Do gráfico, você observa que o tempo entre dois picos consecutivos (período) é T = 10–16 s — f=1/T=1/10-16 — f=1016Hz — R- C
38- V = 1.188km/h = 330 m/s — f = 2.640 Hz — V=λf — λ=V/f=330/2.640 — λ=0,125m
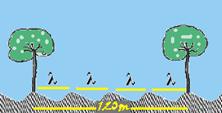
39- Observe na figura que — equação da onda — V=λf — 10=λ.1 — λ=10m — comprimento da ponte —
L=3λ/2 — L=3.10/2 — L=15m
40-
Veja na figura abaixo que um comprimento de onda λ vale — 1,5λ/2=15 — λ=15/1,5=10cm=0,1m — equação
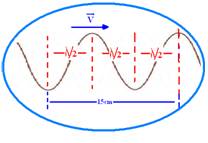
fundamental da ondulatória — V=λf=0,1.740 — V=74m/s.
41-
Observe no gráfico fornecido que o período T (tempo que as ondas superficiais na superfície da água geradas pela aranha demoram para efetuar uma oscilação completa) vale T=4ms=4.10-3s — frequência dessas ondas — f=1/T —
f=1/(4.10-3) — f=0,25.103=250Hz — equação fundamental da ondulatória — v=λf=2.10-3.250 — v=500.10-3m/s — v=0,5m/s=50cm/s — R- B.
42- A velocidade de uma onda eletromagnética no interior do cabo é dada por v = c/n = . Qual é o comprimento de onda de uma onda de frequência f = 400 MHz que se propaga num cabo cujo isolante é o polietileno ( K , = 2,25 )?
Como a velocidade da luz no vácuo (e aproximadamente no ar) é constante — v= λ.f =constante — para que λ.f seja constante eles devem ser inversamente proporcionais, ou seja, à menor frequência f está associada ao maior comprimento λ — a haste que apresenta maior comprimento é a última da direita que mede L=30cm=0,3m — como, pelo enunciado, L ≈ λ/2 —
λ =2.L=2.0,3=0,6m — v= λ.f — 3.108= 0,6.f — f=5,0.108 Hz.
43-
– I. Falsa — como as cordas são idênticas, elas possuem a mesma densidade linear μ (massa por unidade de comprimento), mas como as trações T são diferentes, pela expressão V=√(T/μ) as velocidades também devem ser diferentes.
II. Correta — observe no gráfico que γ1= γ2=4m.
III. Falsa — equação fundamental da ondulatória — V= γ..f — se as velocidades são diferentes e γ é o mesmo, as freqüências f devem ser diferentes.
R- B
44-
3 λ/2=0,51 — 3λ=1,02 — λ=0,34m — equação fundamental da ondulatória — V= λf — 340=0,34.f — f=1000Hz — se a distância da pessoa ao obstáculo é d, o som vai e volta percorrendo 2d, com V=340m/s em ∆t=2,0s — V=2d/∆t — 340=2d/2,0 — d=d=340m — R- B.