Exercícios de vestibulares com resoluções comentadas sobre Equação da onda
Exercícios de vestibulares com resoluções comentadas sobre
Equação da onda (Equação fundamental da ondulatória)
01-(UFSM) “Os habitantes dos pinheirais formados por araucárias começaram a produzir cerâmicas e aperfeiçoaram seus instrumentos de trabalho.”
Para descascar e moer cereais, as índias usavam um pilão de pedra. Se uma índia batesse nos cereais 20 vezes por minuto, a freqüência das batidas, em Hz, seria de, aproximadamente,
02-(UFAL) Uma onda produzida numa corda se propaga com freqüência de 25 Hz. O gráfico a seguir representa a corda num dado instante.
Considere a situação apresentada e os dados do gráfico para analisar as afirmações que seguem.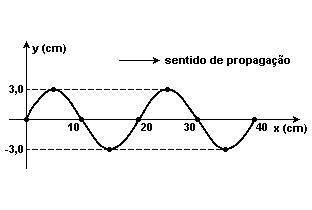
( ) O período de propagação da onda na corda é 20 s.
( ) A amplitude da onda estabelecida na corda é de 6,0cm.
( ) A velocidade de propagação da onda na corda é de 5,0 m/s.
( ) A onda que se estabeleceu na corda é do tipo transversal.
( ) A onda que se estabeleceu na corda tem comprimento de onda de 10 cm.
03- (UFRS) Um trem de ondas senoidais, gerado por um dispositivo mecânico oscilante, propaga-se ao longo de uma corda. A tabela a seguir descreve quatro grandezas que caracterizam essas ondas mecânicas.
As grandezas 1, 2, 3 e 4 são denominadas, respectivamente,
a) freqüência, fase, amplitude e comprimento de onda.
b) fase, freqüência, comprimento de onda e amplitude.
c) período, freqüência, velocidade de propagação e amplitude.
d) período, freqüência, amplitude e comprimento de onda.
e) freqüência, período, comprimento de onda e amplitude
04-(UNESP-SP) A sucessão de pulsos representada na figura foi produzida em 1,5s. Determine a
freqüência e o período da onda.
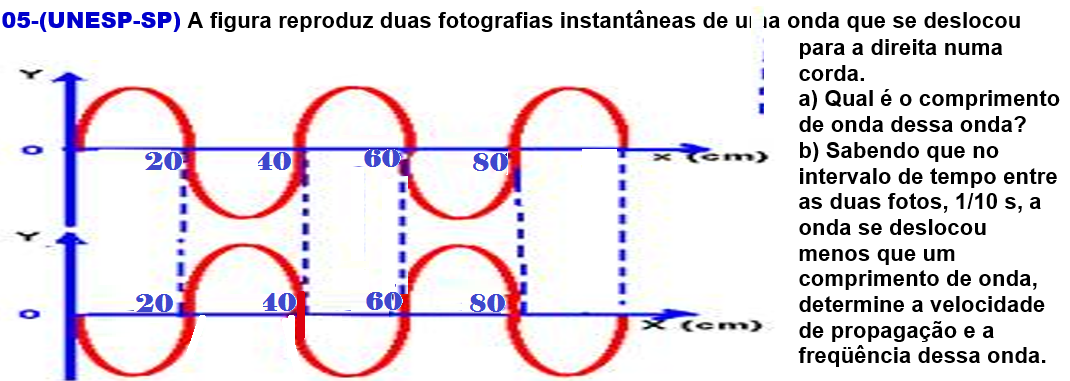
06- (UFPE)
As curvas A e B representam duas fotografias sucessivas de uma onda transversal que se propaga numa corda. O intervalo entre as fotografias é de 0,008 s e é menor do que o período da onda. Calcule a velocidade de propagação da onda na corda, em m/s.
07-(UFRJ-RJ) Uma perturbação periódica em uma corda produz ondas de freqüência 40 Hz e comprimento de onda 15 cm.
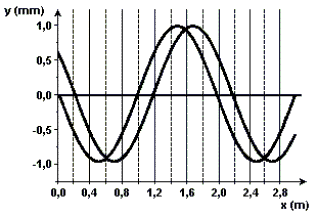
Neste caso, calcule:
a) o período da onda.
b) a velocidade da onda.
08-(UFRJ-RJ) Através de um dispositivo adequado, produzem-se ondas em um meio elástico, de tal modo que as freqüências das ondas obtidas se encontram no intervalo de 15Hz a 60Hz. O gráfico mostra como varia o comprimento de onda (λ) em função da freqüência (f).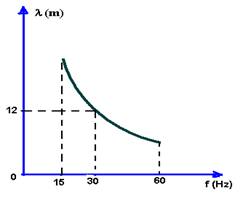
a) Calcule o menor comprimento de onda produzido nessa experiência.
b) Para um comprimento de onda de 12m, calcule o período da onda.
09-(PUC-SP) A velocidade de propagação de uma perturbação transversal numa corda de massa específica linear igual a 0,01kg/m, tracionada por uma força de 64N, é, em metros por segundo, de:
10-(MACKENZIE-SP) Um fio metálico de 2m de comprimento e 10g de massa é tracionado mediante uma força de 200N. Determine a velocidade de propagação de um pulso transversal nesse fio.
11-(FMJ-CE) A figura mostra uma corda de massa m, submetida a uma força de tração de intensidade T=24N, tendo suas extremidades presas a dois suportes fixos A e B.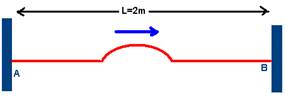
Determine a massa de m, em quilogramas, sabendo que a velocidade de propagação do pulso é V=40m/s.
12-(UFPE) Uma onda transversal propaga-se em um fio de densidade d=10 g/m. O fio está submetido a uma tração F = 16 N. Verifica-se que a menor distância entre duas cristas da onda é igual a 4,0 m. Calcule a freqüência desta onda, em Hz.
13-(UFMS) Uma corda de comprimento L=50cm está tensionada por um peso P=52,9N. (figura)
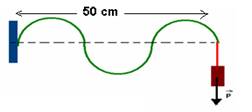
Calcule a velocidade de propagação da onda nessa corda, em m/s.
14-(UFES) Os morcegos emitem ultra-sons (movimento vibratório, cuja freqüência é superior a 20.000 Hz). Considere-se que o menor comprimento de onda emitido por um morcego é de 3,4.
10-3 m.
Supondo-se que a velocidade do som no ar é de 340 m/s, determine a freqüência mais alta que um morcego emite.
15-(FUVEST-SP) Um grande aquário, com paredes laterais de vidro, permite visualizar, na superfície da água, uma onda que se propaga. A figura representa o perfil de tal onda no instante To. Durante sua passagem, uma bóia, em dada posição, oscila para cima e para baixo e seu deslocamento vertical (y), em função do tempo, está representado no gráfico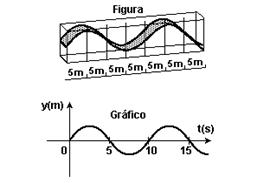
Com essas informações, é possível concluir que a onda se propaga com uma velocidade, aproximadamente, de
a) 2,0 m/s
b) 2,5 m/s
c) 5,0 m/s
d) 10 m/s
e) 20 m/s
16- (UFMG) Daniel brinca produzindo ondas ao bater com uma varinha na superfície de um lago. A varinha toca a água a cada 5 segundos. Se Daniel passar a bater a varinha na água a cada 3 segundos, as ondas produzidas terão maior:
a) comprimento de onda.
b) freqüência.
c) período.
d) velocidade
17- (Fuvest-SP) Radiações, como raios X, luz verde, luz ultravioleta, microondas ou ondas de rádio, são caracterizadas por seu comprimento de onda (λ) e por sua freqüência (f). Quando essas radiações propagam-se no vácuo, todas apresentam o mesmo valor para:
18-(UFPE) A figura a seguir mostra esquematicamente as ondas na superfície d’água de um lago, produzidas por uma fonte de freqüência 6,0 Hz, localizada no ponto A.
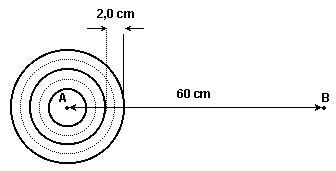
As linhas cheias correspondem às cristas, e as pontilhadas representam os vales em um certo instante de tempo. Qual o intervalo de tempo, em segundos, para que uma frente de onda percorra a distância da fonte até o ponto B, distante 60 cm?
19-(PUC-SP) Em dezembro de 2004 um terremoto no fundo do oceano, próximo à costa oeste da ilha de Sumatra, foi a perturbação necessária para a geração de uma onda gigante, uma “tsunami”. A onda arrasou várias ilhas e localidades costeiras na Índia, no Sri Lanka, na Indonésia, na Malásia, na Tailândia, dentre outras.
Uma “tsunami” de comprimento de onda 150 quilômetros pode se deslocar com velocidade de 750 km/h. Quando a profundidade das águas é grande, a amplitude da onda não atinge mais do que 1 metro, de maneira que um barco nessa região praticamente não percebe a passagem da onda.
Quanto tempo demora para um comprimento de onda dessa “tsunami” passar pelo barco?
20-(FUVEST-SP) Um sensor, montado em uma plataforma da Petrobrás, com posição fixa em relação ao fundo do mar, registra as sucessivas posições de uma pequena bola que flutua sobre a superfície da água, à medida que uma onda do mar passa por essa bola continuamente. A bola descreve um movimento aproximadamente circular, no plano vertical, mantendo-se em torno da mesma posição média, tal como reproduzido na seqüência de registros adiante, nos tempos indicados. O intervalo entre registros é menor do que o período da onda. A velocidade de propagação dessa onda senoidal é de 1,5 m/s.
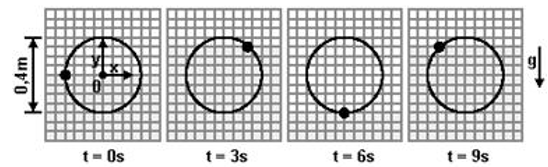
Para essas condições:
a) Determine o período T, em segundos, dessa onda do mar.
b) Determine o comprimento de onda —, em m, dessa onda do mar.
c) Represente, um esquema do perfil dessa onda, para o instante t = 14 s, tal como visto da plataforma fixa. Indique os valores apropriados nos eixos horizontal e vertical.
21-(UNICAMP-SP) Uma das formas de se controlar misturas de gases de maneira rápida, sem precisar retirar amostras, é medir a variação da velocidade do som no interior desses gases. Uma onda sonora com freqüência de 800 kHz é enviada de um emissor a um receptor (vide esquema), sendo então medida eletronicamente sua velocidade de propagação em uma mistura gasosa. O gráfico adiante apresenta a velocidade do som para uma mistura de argônio e nitrogênio em função da fração molar de Ar em N.
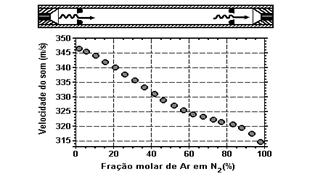
a) Qual o comprimento de onda da onda sonora no N‚ puro?
b) Qual o tempo para a onda sonora atravessar um tubo de 10 cm de comprimento contendo uma mistura com uma fração molar de Ar de 60%?
22- (UNICAMP-SP) O sistema GPS (“Global Positioning System”) consiste em um conjunto de satélites em órbita em torno da Terra que transmitem sinais eletromagnéticos para receptores na superfície terrestre. A velocidade de propagação dos sinais é de 300.000 km/s. Para que o sistema funcione bem, a absorção atmosférica desse sinal eletromagnético deve ser pequena. A figura a seguir mostra a porcentagem de radiação eletromagnética absorvida pela atmosfera em função do comprimento de onda
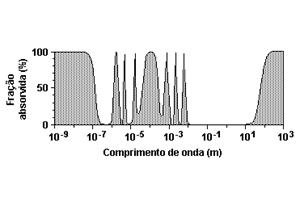
a) A freqüência do sinal GPS é igual a 1.500 MHz. Qual o comprimento de onda correspondente? Qual a porcentagem de absorção do sinal pela atmosfera?
b) Uma das aplicações mais importantes do sistema GPS é a determinação da posição de um certo receptor na Terra. Essa determinação é feita através da medida do tempo que o sinal leva para ir do satélite até o receptor. Qual é a variação Dt na medida do tempo feita pelo receptor que corresponde a uma variação na distância satélite-receptor de Dx = 100m? Considere que a trajetória do sinal seja retilínea.
23-(UNICAMP-SP) Ondas são fenômenos nos quais há transporte de energia sem que seja necessário o transporte de massa. Um exemplo particularmente extremo são os “tsunamis”, ondas que se formam no oceano, como conseqüência, por exemplo, de terremotos submarinos.
a) Se, na região de formação, o comprimento de onda de um”tsunami” é de 150 km e sua velocidade é de 200 m/s, qual é o período da onda?
b) A velocidade de propagação da onda é dada por v =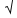 
(gh) , onde h é a profundidade local do oceano e g é a aceleração da gravidade (10m/s2). Qual é a velocidade numa região próxima à costa, onde a profundidade é de 6,4 m?
c) Sendo A a amplitude (altura) da onda e supondo-se que a energia do “tsunami” se conserva, o produto V.A2 mantém-se constante durante a propagação. Se a amplitude da onda na região de formação for de 1,0 m, qual será a amplitude perto da costa, onde a profundidade é de 6,4 m?
24-(UNIFESP-SP) O gráfico representa a profundidade (y) no mar em função da velocidade do som (v). A freqüência do som é de 3000 Hz; essa curva é válida para condições determinadas de pressão e salinidade da água do mar.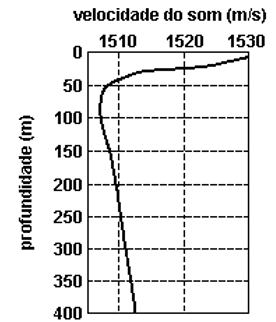
a) Nessas condições, faça uma avaliação aproximada do valor mínimo atingido pela velocidade do som no mar e da profundidade em que isso ocorre.
b) Desenhe na folha de respostas o esboço do correspondente gráfico profundidade (y) em função do comprimento de onda (—) do som. Adote o mesmo eixo e a mesma escala para a profundidade e coloque o comprimento de onda no eixo das abscissas. Represente três valores de —, escritos com três algarismos significativos.
25-(UNESP-SP) A propagação de uma onda no mar da esquerda para a direita é registrada em intervalos de 0,5 s e apresentada através da seqüência dos gráficos da figura, tomados dentro de um mesmo ciclo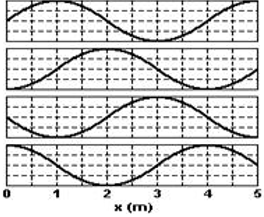
Analisando os gráficos, podemos afirmar que a velocidade da onda, em m/s, é de
a) 1,5.
b) 2,0.
c) 4,0.
d) 4,5.
e) 5,0.
26-(UNICAMP-SP) O diagnóstico precoce de doenças graves, como o câncer, aumenta de maneira significativa a chance de cura ou controle da doença. A tomografia de Ressonância Magnética Nuclear é uma técnica de diagnostico médico que utiliza imagens obtidas a partir da absorção de radiofreqüência pelos prótons do hidrogênio submetidos a um campo magnético. A condição necessária para que a absorção ocorra, chamada condição de ressonância, é dada pela equação f =λB, sendo f a frequência da radiação, B o campo magnético na posição do próton, e λ= 42 MHz/T
Para se mapear diferentes partes do corpo, o campo magnético aplicado varia com a posição ao longo do corpo do paciente.
a) Observa-se que a radiação de freqüência igual a 63MHz é absorvida quando um paciente é submetido a um campo magnético que varia conforme o gráfico acima. Em que posição x do corpo do paciente esta absorção ocorre?
b) O comprimento de onda é a distância percorrida pela onda durante o tempo de um período. O período é igual ao inverso da freqüência da onda. Qual é o comprimento de onda da radiofreqüência de 63 MHz no ar, sabendo-se que sua velocidade é igual a 3,0 . 108 m/s?
27-(UNESP-SP) Considere um lago onde a velocidade de propagação das ondas na superfície não
dependa do comprimento de onda, mas apenas da profundidade. Essa relação pode ser dada por v =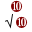 
gd) , onde g é a aceleração da gravidade e d é a profundidade. Duas regiões desse lago têm diferentes profundidades, como ilustrado na figura.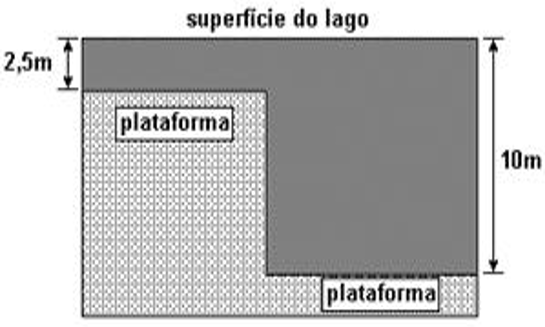
O fundo do lago e formado por extensas plataformas planas em dois níveis; um degrau separa uma região com 2,5 m de profundidade de outra com 10 m de profundidade. Uma onda plana, com comprimento de onda l, forma-se na superfície da região rasa do lago e propaga-se para a direita, passando pelo desnível. Considerando que a onda em ambas as regiões possui mesma freqüência, pode-se dizer que o comprimento de onda na região mais profunda é (g=10m/s2)
28-(FUVEST-SP) A propagação de ondas na água é estudada em grandes tanques, com detectores e softwares apropriados. Em uma das extremidades de um tanque (Figura 1), de 200 m de comprimento, um dispositivo D produz ondas na água, sendo que o perfil da superfície da água, ao longo de toda a extensão do tanque, é registrado por detectores em instantes subseqüentes. Um conjunto de ondas, produzidas com freqüência constante, tem seu deslocamento y, em FUNÇÃO DO TEMPO, representado na Figura 1, tal como registrado por detectores fixos na posição x = 15 m.
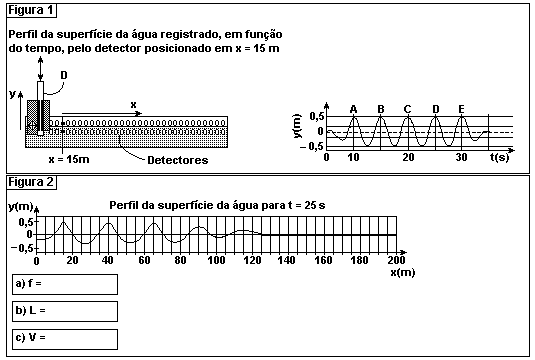Para esse mesmo conjunto de ondas, os resultados das medidas de sua propagação ao longo do tanque são apresentados a seguir. Esses resultados correspondem aos deslocamentos y do nível da água em relação ao nível de equilíbrio (y = 0) medidos no instante t = 25 s para diversos valores de x. A partir desses resultados:
a) Estime a freqüência f, em Hz, com que as ondas foram produzidas.
b) Estime o comprimento de onda L, em metros, das ondas formadas.
c) Estime a velocidade V, em m/s, de propagação das ondas no tanque.
d) Identifique, no gráfico da Figura 2 (t = 25 s), as posições das ondas A, B, C, D e E, assinaladas na Figura 1, ainda que, como pode ser observado, as amplitudes dessas ondas diminuam com sua propagação.
29-(FUVEST-SP) Um vibrador produz, numa superfície líquida, ondas de comprimento 5,0cm que se propagam a velocidade de 3,0cm/s.
a) Qual a freqüência das ondas?
b) Caso o vibrador aumente apenas sua amplitude de vibração, o que ocorre com a velocidade de propagação, o comprimento e a freqüência das ondas?
30-(FUVEST-SP) Num lago o vento produz ondas periódicas que se propagam com a velocidade de 2m/s. O comprimento de onda é 10m. Determine o período de oscilação de um barco
a) quando ancorado nesse lago.
b) quando se movimenta em sentido contrário ao da propagação das ondas, com uma velocidade de 8m/s.
31-(UECE-CE)
Fornos de micro-ondas usam ondas de rádio de comprimento de onda aproximadamente 12 cm para aquecer os alimentos.
Considerando a velocidade da luz igual a 300 000 km/s a frequência das ondas utilizadas é
a) 360 Hz.
b) 250 kHz.
c) 3,6 MHz.
d) 2,5 GHz.
32-(PUC-PR)
Para que um objeto possa ser visível em um microscópio qualquer, o comprimento de onda da radiação incidente deve ser pelo menos comparável ao tamanho do objeto. Na física quântica, o princípio da dualidade onda-partícula, introduzido por Louis de Broglie, propõe que partículas de matéria, como os elétrons, podem comportar-se como ondas de maneira similar à luz. Um exemplo de aplicação desse princípio é o que ocorre no microscópio eletrônico, em que um feixe de elétrons é produzido para “iluminar” a amostra. O comprimento de onda dos elétrons do feixe é muito menor que o da luz; com isso, consegue-se obter ampliações mil vezes maiores do que as de um microscópio óptico.
Suponha que, para visualizar o vírus H1N1 em um microscópio eletrônico, um feixe de elétrons tenha sido ajustado para fornecerelétrons que se propagam com comprimento de onda igual ao diâmetro do vírus (supondo forma esférica). Se a velocidade de propagação da onda do feixe for de 104 m/s e a frequência for de 1011 Hz, assinale a alternativa que corresponde ao diâmetro do vírus H1N1. Dado: 1 nm (nanômetro) = 10-9 m.
a) 10 nm
b) 1 nm
c) 100 nm
d) 10 µm
e) 1 µm
33-(FGV-SP)
Veja esse quadro. Nele, o artista mostra os efeitos dos golpes intermitentes do vento sobre um trigal.
Admitindo que a distância entre as duas árvores seja de 120 m e, supondo que a frequência dos golpes de ar e consequentemente do trigo balançando seja de 0,50 Hz, a velocidade do vento na ocasião retratada pela pintura é, em m/s,
34-(UPE-PE)
Um pulso ondulatório senoidal é produzido em uma extremidade de uma corda longa e se propaga por toda a sua extensão. A onda possui uma frequência de 50 Hz e comprimento de onda 0,5 m. O tempo que a onda leva para percorrer uma distância de 10m na corda vale em segundos:
35-(PUC-SP) O fone de ouvido tem se tornado cada vez mais um acessório indispensável para os adolescentes que curtem suas músicas em todos os ambientes e horários. Antes do advento do iPod e outros congêneres, para ouvir as músicas da parada de sucessos, os jovens tinham que carregar seu radinho portátil sintonizado em FM (frequência modulada).
Observando o painel de um desses rádios, calcule a razão aproximada entre o maior e o menor comprimento de onda para a faixa de valores correspondentes a FM.
36-(CPS)
Na Copa do Mundo de 2010, a Fifa determinou que nenhum atleta poderia participar sem ter feito uma minuciosa avaliação cardiológica prévia. Um dos testes a ser realizado, no exame ergométrico, era o eletrocardiograma. Nele é feito o registro da variação dos potenciais elétricos gerados pela atividade do coração.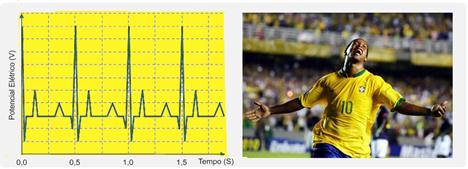
Considere a figura que representa parte do eletrocardiograma de um determinado atleta.
Sabendo que o pico máximo representa a fase final da diástole, conclui-se que a frequência cardíaca desse atleta é, em batimentos por minuto,
a) 60.
b) 80.
c) 100.
d) 120.
e) 140.
37-(FUVEST-SP)
Em um ponto fixo do espaço, o campo elétrico de uma radiação eletromagnética tem sempre a mesma direção e oscila no tempo, como mostra o gráfico abaixo, que representa sua projeção E nessa direção fixa; E é positivo ou negativo conforme o sentido do campo.
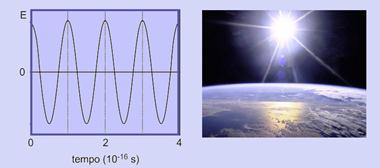
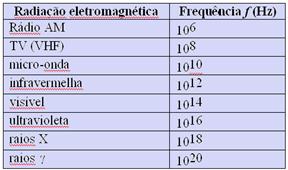
Consultando a tabela acima, que fornece os valores típicos de frequência f para diferentes regiões do espectro eletromagnético, e analisando o gráfico de E em função do tempo, é possível classificar essa radiação como
38-(UERJ-RJ) A sirene de uma fábrica produz sons com frequência igual a 2640 Hz.
Determine o comprimento de onda do som produzido pela sirene em um dia cuja velocidade de propagação das ondas sonoras no ar seja igual a 1.188 km/h.
39-(UFPR-PR) Uma fila de carros, igualmente espaçados, de tamanhos e massas iguais faz a travessia de uma ponte com velocidades iguais e constantes, conforme mostra a figura abaixo. Cada vez que um carro entra na ponte, o impacto de seu peso provoca nela uma perturbação em forma de um pulso de onda. Esse pulso se propaga com velocidade de módulo 10 m/s no sentido de A para B. Como resultado, a ponte oscila, formando uma onda estacionária com 3 ventres e 4 nós.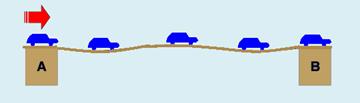
Considerando que o fluxo de carros produza na ponte uma oscilação de 1 Hz, assinale a alternativa correta para o comprimento da ponte.
40-(UFPE-PE)
Na figura abaixo, mostra-se uma onda mecânica se propagando em um elástico submetido a um
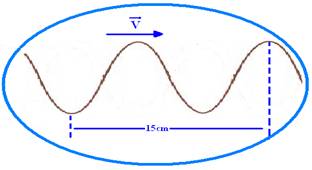
certa tensão, na horizontal. A freqüência da onda é f = 740 Hz.
Calcule a velocidade de propagação da onda, em m/s.
41-(IFNMG-MG)
Algumas aranhas, valendo-se da tensão superficial, podem caminhar sobre a superfície livre da água. Para atrair eventuais presas, a aranha produz pequenas vibrações, gerando ondas superficiais, as quais apresentam comprimento de onda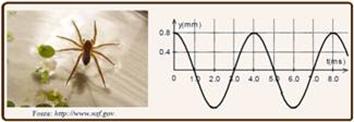
igual a 2,0 mm. O deslocamento vertical das partículas de água varia com o tempo (dado em milissegundos, ms) conforme o gráfico apresentado na figura acima.
Nessas condições, o valor da velocidade de propagação de tais ondas, expresso em cm/s, está corretamente apresentado na alternativa:
42-(UNICAMP-SP)
Nos últimos anos, o Brasil vem implantando em diversas cidades o sinal de televisão digital. O sinal de televisão é transmitido
através de antenas e cabos, por ondas eletromagnéticas cuja velocidade no ar é aproximadamente igual à da luz no vácuo.
Um tipo de antena usada na recepção do sinal é a log-periódica, representada na figura abaixo, na qual o comprimento das hastes metálicas de uma extremidade à outra, L , é variável. A maior eficiência de recepção é obtida quando L é cerca de meio comprimento de onda da onda eletromagnética que transmite o sinal no ar ( L ≈ λ/2 ). Encontre a menor frequência que a antena ilustrada na figura consegue sintonizar de forma eficiente, e marque na figura a haste correspondente.
43-(FUVEST-SP)
A figura abaixo representa imagens instantâneas de duas cordas flexíveis idênticas, C1 e C2, tracionadas por forças diferentes, nas quais se propagam ondas.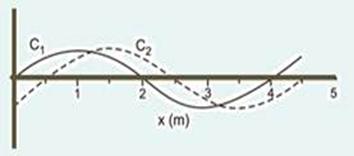
Durante uma aula, estudantes afirmaram que as ondas nas cordas C1 e C2 têm:
I. A mesma velocidade de propagação.
II. O mesmo comprimento de onda.
III. A mesma frequência.
Está correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
44-(COLÉGIO NAVAL)
Analise a figura a seguir.
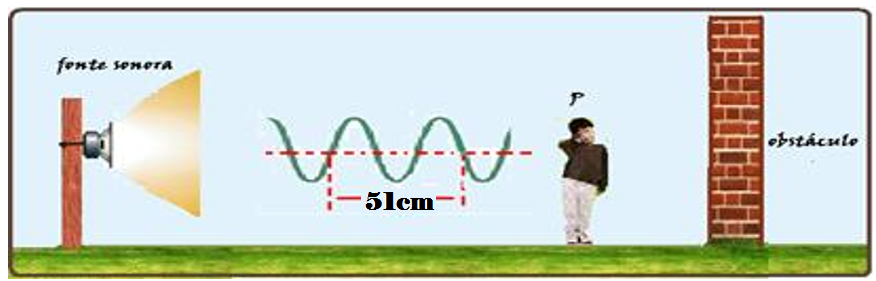
Uma pessoa encontra-se parada em um ponto P, distante de um obstáculo e de uma fonte sonora que emite ondas conforme a configuração mostrada na figura acima. Um som emitido pela fonte no instante to = Os passa pelo ponto P no instante t1 = 0,5 s e retorna ao ouvido da pessoa no instante t2 =2,5s, após ter colidido com o obstáculo. Considerando a velocidade do som no ar como sendo constante e igual a 340m/ s, é correto afirmar que o comprimento de onda, a frequência da fonte emissora e a distância da pessoa até o obstáculo valem, respectivamente:
(A) λ=0,17m; f =1000Hz; d = 170m
(B) λ = 0,34m; f =1000Hz; d=340m.
(C) λ =0,34m; f=2000Hz; d=170m
(D) λ =0,51m; f=1000Hz; d=340m
(E) λ =0, 51m; f =2000Hz; d=680m