Equação da onda (Equação fundamental da ondulatória)
Equação da onda (Equação fundamental da ondulatória)
Elementos de uma onda
Considere a onda periódica (sucessão de pulsos iguais em tempos iguais) das figurasa seguir, cujas principais características são:
![]() Comprimento de onda (λ)
Comprimento de onda (λ) ![]() representa a distância percorrida pela onda até começar novamente a repetição, ou seja, é a menor distância entre dois pontos consecutivos que estão em concor-dância de fase, como por exemplo, a menor distância entre duas cristas ou dois vales.
representa a distância percorrida pela onda até começar novamente a repetição, ou seja, é a menor distância entre dois pontos consecutivos que estão em concor-dância de fase, como por exemplo, a menor distância entre duas cristas ou dois vales.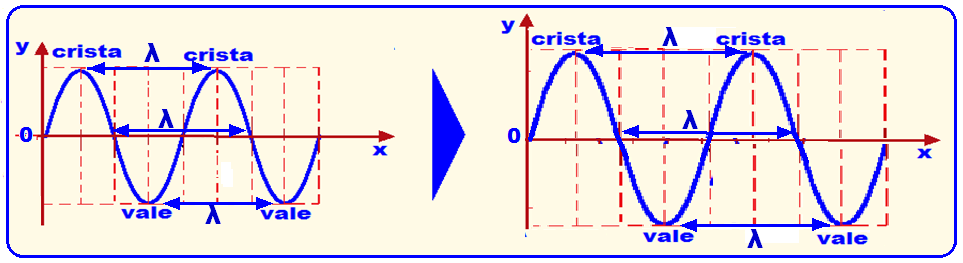
![]() Período (T)
Período (T) ![]() tempo que a onda demora para percorrer um comprimento de onda (1λ), que é o mesmo tempo que um ponto qualquer da onda demora para efetuar uma oscilação (vai e vem) completa e que é o mesmo tempo que a fonte demora para gerar uma onda completa.
tempo que a onda demora para percorrer um comprimento de onda (1λ), que é o mesmo tempo que um ponto qualquer da onda demora para efetuar uma oscilação (vai e vem) completa e que é o mesmo tempo que a fonte demora para gerar uma onda completa.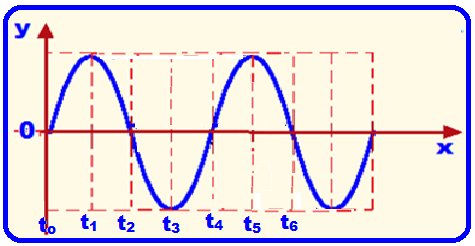
Na figura acima, o período T é o tempo compreendido entre os instantes T = t4 – to = t5 – t1 = t6 – t2, etc.
![]() Frequência (f)
Frequência (f) ![]() A frequência (f) representa quantas oscilações completas uma onda efetua
A frequência (f) representa quantas oscilações completas uma onda efetua
em cada unidade de tempo, ou ainda, quantos comprimentos de onda passam por um ponto da onda em cada unidade de tempo.
Se o período T estiver em segundos (s) a freqüência estará em hertz (Hz), que significa ciclos por segundo.
Exemplo: Se a frequência de uma onda for de 60 Hz, isto significa que a fonte ou qualquer ponto desta onda oscila 60 vezes em cada segundo.
Relação importante
Velocidade V de propagação da onda (Equação fundamental da ondulatória)
Supondo o meio homogêneo, a onda se propaga nele com velocidade constante, dada por
V =  S/
S/ t.
t.
Mas, observe que, quando  S = 1λ,
S = 1λ,  t = T, pois o período T é o tempo que a onda demora para percorrer um comprimento de onda (1λ).
t = T, pois o período T é o tempo que a onda demora para percorrer um comprimento de onda (1λ).
V =  S/
S/ t
t ![]() V = λ/T
V = λ/T ![]() V = λ/(1/f)
V = λ/(1/f) ![]() V = λ.f (essa equação é chamada equação fundamental da ondulatória).
V = λ.f (essa equação é chamada equação fundamental da ondulatória).

Velocidade de propagação dos pulsos nos meios unidimensionais (corda)
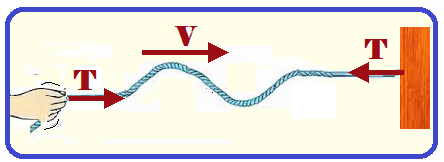
Considere um pulso ou vários pulsos sucessivos (onda) se propagando com velocidade V numa
corda tracionada (esticada) por uma força de intensidade F.
Denominamos densidade linear de massa (µ) de uma corda homogênea, de seção transversal constante, que possui massa (m) e comprimento (L), à expressão:
Significado físico de µ ![]() significa quanto de massa a corda tem por unidade de comprimento. Assim, uma corda de 0,5 kg/m possui, no SI, 0,5kg de massa para cada 1 metro de comprimento.
significa quanto de massa a corda tem por unidade de comprimento. Assim, uma corda de 0,5 kg/m possui, no SI, 0,5kg de massa para cada 1 metro de comprimento.

A velocidade (V) de propagação do pulso na corda é dada, também por:
Onde T é a intensidade da força que traciona (estica) a corda e µ é a densidade linear de massa da mesma.
Observe que V é diretamente proporcional a 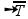 , ou seja, quanto mais esticada estiver a corda, maior será a velocidade de propagação do pulso ou da onda na mesma e que V é inversamente proporcional a
, ou seja, quanto mais esticada estiver a corda, maior será a velocidade de propagação do pulso ou da onda na mesma e que V é inversamente proporcional a 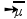 , ou seja, quanto maior a densidade linear da corda, menor será a velocidade de propagação da onda na mesma.
, ou seja, quanto maior a densidade linear da corda, menor será a velocidade de propagação da onda na mesma.
Propagação de ondas em meios bidimensionais
Podem ser de dois tipos:
![]()
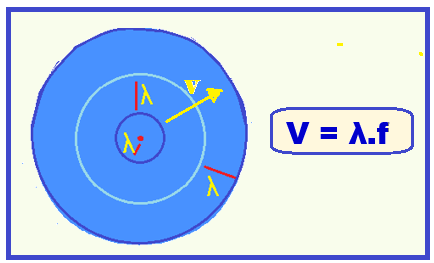
Ondas circulares (esféricas) ![]() Quando a ponta da régua bate continua e periodicamente na superfície da água origina perturbações circulares (ondas circulares) que se movem na superfície da água, afastando-se do ponto onde as perturbações são geradas.
Quando a ponta da régua bate continua e periodicamente na superfície da água origina perturbações circulares (ondas circulares) que se movem na superfície da água, afastando-se do ponto onde as perturbações são geradas.
A frente de onda ou superfície de onda é o lugar geométrico de todos os pontos que estão em concordância de fase de vibração, como por exemplo, duas cristas ou dois vales.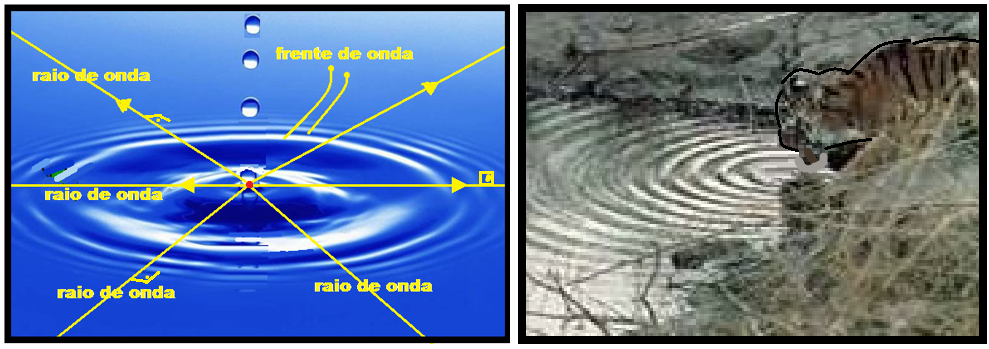
O raio de onda é toda reta perpendicular às frentes de onda e que indicam a direção e o sentido de propagação dessas ondas.
O comprimento de onda (λ) é a distância entre duas frentes de onda consecutivas.
![]()
Ondas planas (retas)
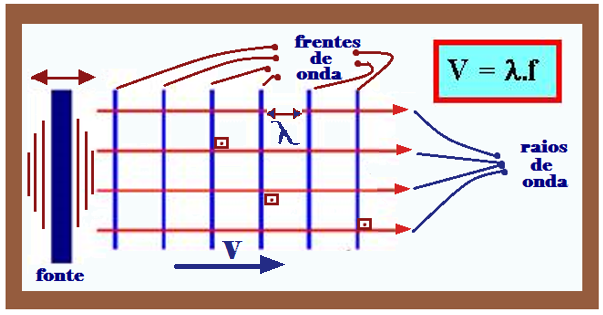
Produzidas tocando-se leve e continuamente a superfície da água com uma régua (fonte) na posição indicada na figura.
Observe que as frentes de ondas e os raios de onda são retas paralelas e consequentemente perpendiculares.
O comprimento de onda (λ) é a distância entre duas frentes de onda (cristas ou vales) consecutivas.
O que você deve saber, informações e dicas
![]()
Amplitude da onda (A)
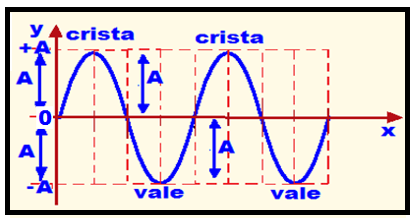
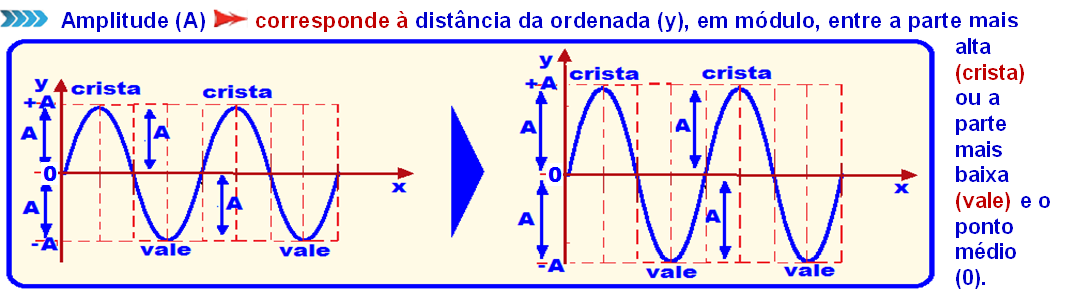
Amplitude (A) ![]() corresponde à distância da ordenada (Y), em módulo, entre a parte mais alta (crista) ou a parte mais baixa (vale) e o ponto médio (0).
corresponde à distância da ordenada (Y), em módulo, entre a parte mais alta (crista) ou a parte mais baixa (vale) e o ponto médio (0).
![]()
Comprimento de onda (λ)
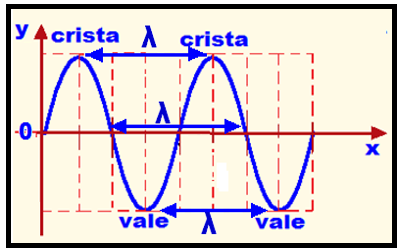
Representa a distância percorrida pela onda até começar novamente a repetição, ou seja, é a menor distância entre dois pontos consecutivos que estão em concordância de fase, como por exemplo a menor distância entre duas cristas ou dois vales.
![]()
Período (T) ![]() tempo que a onda demora para percorrer um comprimento de onda (1λ), que é o mesmo tempo que um ponto qualquer da onda demora para oscilação (vai e vem) completa e que é o mesmo tempo que a fonte demora para gerar uma onda completa.
tempo que a onda demora para percorrer um comprimento de onda (1λ), que é o mesmo tempo que um ponto qualquer da onda demora para oscilação (vai e vem) completa e que é o mesmo tempo que a fonte demora para gerar uma onda completa.
![]()
Freqüência (f) ![]() representa quantas oscilações completas uma onda efetua em cada unidade de tempo, ou ainda, quantos comprimentos de onda completos passam por um ponto da onda em cada unidade de tempo.
representa quantas oscilações completas uma onda efetua em cada unidade de tempo, ou ainda, quantos comprimentos de onda completos passam por um ponto da onda em cada unidade de tempo.
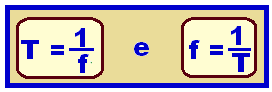
Se o período T estiver em segundos (s) a freqüência estará em hertz (Hz), que significa ciclos por segundo e a relação entre f e T está abaixo:

![]()

![]()
Fórmulas

![]()
Se o meio é o mesmo, V, λ e f também são os mesmos.
![]()
A amplitude A não está relacionada com V, f e λ, mas apenas com a quantidade de energia transportada pela onda. Quanto maior a energia, maior a amplitude e vice-versa.
![]()
Ondas bidimensionais circulares

![]()
Ondas bidimensionais planas

![]()
Ondas em meios tridimensionais A onda se propaga no espaço e em todas as direções. Exemplo: Ondas sonoras e luz.
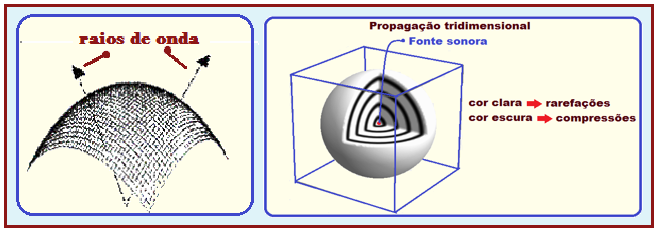
As frentes de onda são esferas e os raios de onda são radiais e saem da fonte de perturbação em todas as direções.
![]() Exercícios interessantes os quais você deve conferir:
Exercícios interessantes os quais você deve conferir:
01-(FUVEST-SP) Num lago o vento produz ondas periódicas que se propagam com a velocidade
de 2m/s. O comprimento de onda é 10m. Determine o período de oscilação de um barco:
a) quando ancorado nesse lago.
b) quando se movimenta em sentido contrário ao da propagação das ondas, com uma velocidade de 8m/s.
Resolução:
a) Com o barco ancorado (parado) ![]() V = 2 m/s
V = 2 m/s ![]() λ = 10 m
λ = 10 m ![]() equação fundamental da ondulatória
equação fundamental da ondulatória![]() V = λ.f
V = λ.f ![]() 2 = 10.f
2 = 10.f ![]() f = 0,2 Hz
f = 0,2 Hz ![]() T = 1/f
T = 1/f ![]() T = 1/0,2
T = 1/0,2 ![]() T = 5 s.
T = 5 s.
b) Como se movem em sentido contrário a velocidade relativa entre o barco e a onda é de V = 2 + 8 ![]() V = 10 m/s.
V = 10 m/s.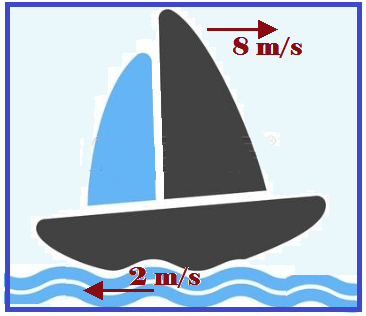
O comprimento de onda continua o mesmo λ = 10 m = ΔS ![]() então, para percorrer ΔS = λ = 10 m a onda deve demorar o tempo de um período Δt = T com velocidade de V = 10 m/s
então, para percorrer ΔS = λ = 10 m a onda deve demorar o tempo de um período Δt = T com velocidade de V = 10 m/s ![]() V = ΔS/Δt
V = ΔS/Δt ![]()
10 = 10/T ![]() T = 1 s.
T = 1 s.

Utilizando a expressão fornecida V = 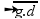 :
:
Na parte mais rasa ![]() V1 =
V1 = 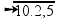
![]() V1 = 5 m/s.
V1 = 5 m/s.
Na parte mais profunda ![]() V2
V2 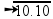
![]() V2 = 10 m/s.
V2 = 10 m/s.
Como, pelo enunciado a frequência f é a mesma ![]() V1 = λ1.f
V1 = λ1.f ![]() 5 = λ1.f
5 = λ1.f ![]() f = 5/λ1 (I)
f = 5/λ1 (I) ![]() V2 = λ2.f
V2 = λ2.f ![]() 10 = λ2.f
10 = λ2.f ![]() f = 10/λ2 (II).
f = 10/λ2 (II).
Igualando (I) com (II) ![]() 5/λ1 = 10/λ2
5/λ1 = 10/λ2 ![]() 5λ2 = 10λ1
5λ2 = 10λ1 ![]() λ2 = 2λ1.
λ2 = 2λ1.
R – B
03-(UNICAMP-SP) O sistema GPS (“Global Positioning System”) consiste em um conjunto de satélites em órbita em torno da Terra que transmitem sinais eletromagnéticos para receptores na superfície terrestre.
A velocidade de propagação dos sinais é de 300.000 km/s. Para que o sistema funcione bem, a absorção atmosférica desse sinal eletromagnético deve ser pequena.
A figura a seguir mostra a porcentagem de radiação eletromagnética absorvida pela atmosfera em função do comprimento de onda.
a) A freqüência do sinal GPS é igual a 1.500 MHz. Qual o comprimento de onda correspondente? Qual a porcentagem de absorção do sinal pela atmosfera?
b) Uma das aplicações mais importantes do sistema GPS é a determinação da posição de um certo receptor na Terra.
Essa determinação é feita através da medida do tempo que o sinal leva para ir do satélite até o receptor.
Qual é a variação Δt na medida do tempo feita pelo receptor que corresponde a uma variação na distância satélite-receptor de Δx = 100m? Considere que a trajetória do sinal seja retilínea.
Resolução:
a) São dados ![]() V = 300.000 km/s = 3.108 m/s e f = 1.500MHz = 1500.106 Hz.
V = 300.000 km/s = 3.108 m/s e f = 1.500MHz = 1500.106 Hz.
Aplicando a equação fundamental da ondulatória V = λf ![]() 3.108 = λ.1.500.106
3.108 = λ.1.500.106 ![]() λ = 2,0.10-1m.
λ = 2,0.10-1m.
Veja pelo gráfico que para esse comprimento de onda (λ = 2,0.10-1m), a porcentagem (fração) de absorção do sinal pela atmosfera é nula
b) Δx = ΔS =100m ![]() V = ΔS/Δt
V = ΔS/Δt ![]() 3.108 = 100/Δt
3.108 = 100/Δt ![]() Δt = 3,3.10-7 s
Δt = 3,3.10-7 s
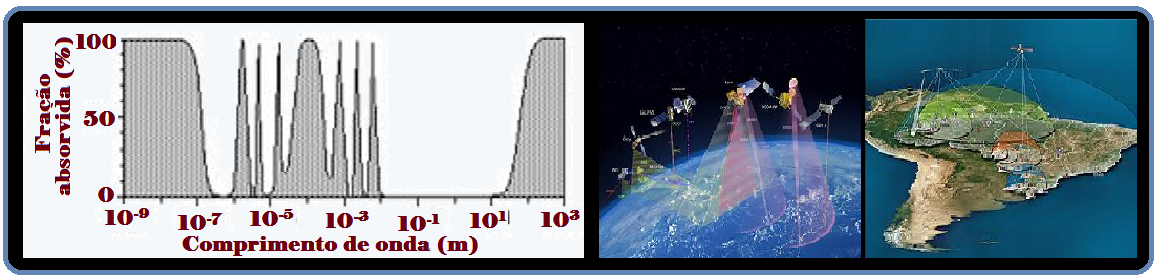
04-(FUVEST-SP) Um sensor, montado em uma plataforma da Petrobrás, com posição fixa em relação ao fundo do mar, registra as sucessivas posições de uma pequena bola que flutua sobre a superfície da água, à medida que uma onda do mar passa por essa bola continuamente.
A bola descreve um movimento aproximadamente circular, no plano vertical, mantendo-se em torno da mesma posição média, tal como reproduzido na seqüência de registros adiante, nos tempos indicados. O intervalo entre registros é menor do que o período da onda.
A velocidade de propagação dessa onda senoidal é de 1,5 m/s.
Para essas condições: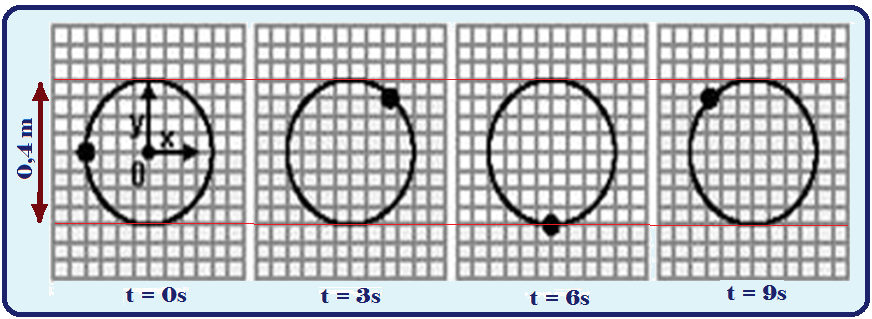
a) Determine o período T, em segundos, dessa onda do mar.
b) Determine o comprimento de onda 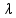 , em m, dessa onda do mar.
, em m, dessa onda do mar.
c) Represente, um esquema do perfil dessa onda, para o instante t = 14 s, tal como visto da plataforma fixa. Indique os valores apropriados nos eixos horizontal e vertical.
Resolução:
a) Trata-se de uma onda mista, pois oscila na horizontal e na vertical e estas oscilações numa onda mista ocorrem no mesmo tempo nestas duas direções.

Observe nas figuras acima, que o intervalo de tempo de 6s corresponde a três quartos do período T, ou seja, T=8s.
b) f=1/T ![]() f = (1/8) Hz
f = (1/8) Hz ![]() V = λ.f
V = λ.f ![]() 1,5 = λ.(1/8)
1,5 = λ.(1/8) ![]() λ = 12 m.
λ = 12 m.
c)
05-(UFRJ-RJ) Através de um dispositivo adequado produzem-se ondas em um meio elástico, de tal modo que as freqüências das ondas obtidas se encontram no intervalo de 15Hz a 60Hz. O gráfico mostra como varia o comprimento de onda (λ) em função da freqüência (f).
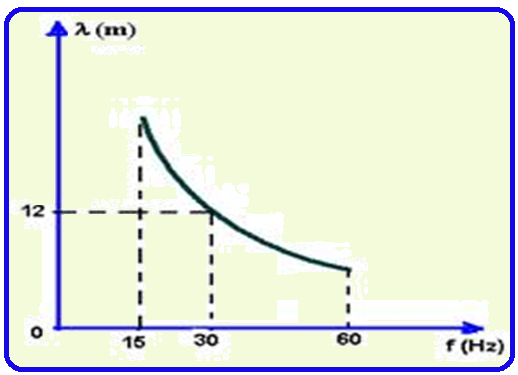
a) Calcule o menor comprimento de onda produzido nessa experiência.
b) Para um comprimento de onda de 12m, calcule o período da onda.
Resolução:
a) Quando f = 30 Hz, λ = 12 m ![]() equação fundamental da ondulatória
equação fundamental da ondulatória ![]() V =
V =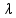 .f
.f ![]() V = 12.30
V = 12.30 ![]()
V = 360m/s (constante-mesmo meio).
O menor λ ocorre quando f = 60 Hz (vide gráfico) ![]() 360 = λ.60
360 = λ.60 ![]() λmínimo = 6 m.
λmínimo = 6 m.
b) Quando λ = 12 m, f = 30 Hz ![]() T = 1/f
T = 1/f ![]() T = (1/30) s.
T = (1/30) s.
06-(FUVEST-SP) Um grande aquário, com paredes laterais de vidro, permite visualizar, na superfície da água, uma onda que se propaga.
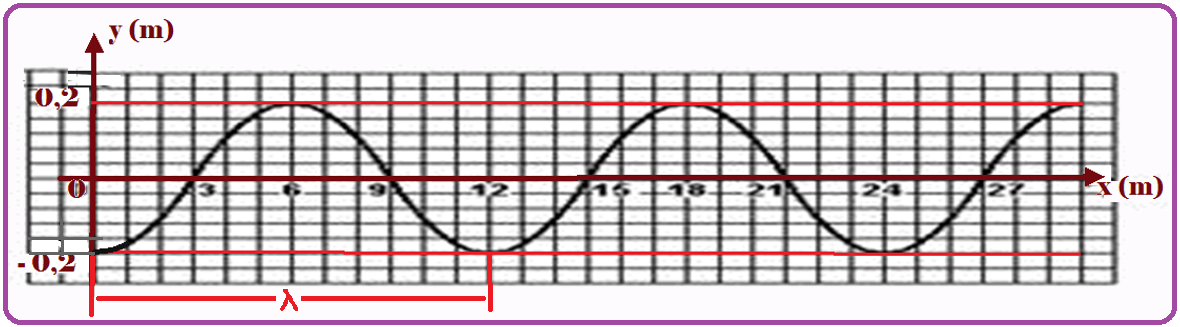
A figura representa o perfil de tal onda no instante To. Durante sua passagem, uma bóia, em dada posição, oscila para cima e para baixo e seu deslocamento vertical (y), em função do tempo, está representado no gráfico
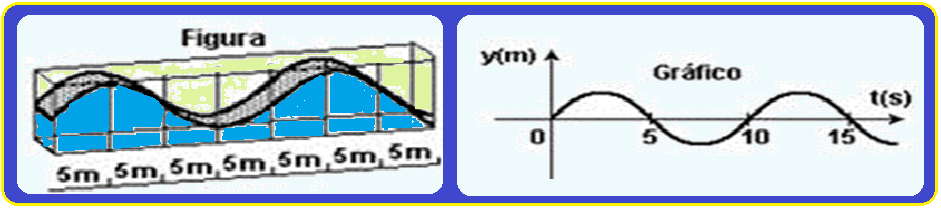
Calcule, com essas informações, a velocidade de propagação da onda.
Resolução:
Da figura, o comprimento de onda λ pode ser a distância entre duas cristas sucessivas ![]() λ = 20 m.
λ = 20 m.
Do gráfico, o período T é o intervalo de tempo que a onda demora para começar a repetição ![]() T =
T =
10 s ![]() f = 1/T
f = 1/T ![]() f = (1/10) Hz.
f = (1/10) Hz.
Equação fundamental da ondulatória ![]() V = λ.f
V = λ.f ![]() V =20.(1/10)
V =20.(1/10) ![]() V = 2,0m/s.
V = 2,0m/s.
