Wave equation (Fundamental wave equation) – EN
Wave equation (Fundamental wave equation)
Elements of a wave
Consider the periodic wave (succession of equal pulses at equal times) in the following figures, whose main characteristics are:
Wavelength (λ ) represents the distance traveled by the wave until it starts repeating again, that is, it is the shortest distance between two consecutive points that are in phase agreement, such as, for example, the shortest distance between two crests or two troughs. 
Period (T) time it takes for the wave to travel one wavelength (1λ), which is the same time it takes for any point on the wave to perform a complete oscillation (back and forth) and which is the same time it takes for the source to generate a complete wave. 
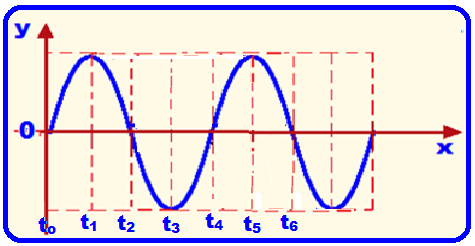
In the figure above, the period T is the time between the instants T = t 4 – t o = t 5 – t 1 = t 6 – t 2 , etc.
Frequency (f) Frequency (f) represents how many complete oscillations a wave makes.
in each unit of time, or how many wavelengths pass through a point on the wave in each unit of time.
If the period T is in seconds (s) the frequency will be in hertz (Hz), which means cycles per second.
Example: If the frequency of a wave is 60 Hz , this means that the source or any point of this wave oscillates 60 times every second.
Important relationship
Wave propagation speed V (Fundamental wave equation)
Assuming the medium is homogeneous, the wave propagates in it with constant speed , given by
V = 
S/ t.
But note that when S = 1λ, t = T , since the period T is the time it takes for the wave to travel one wavelength (1λ).
V = 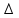S/ 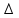t V = λ /T V = λ /(1/f) V = λ .f (this equation is called the fundamental wave equation).
Pulse propagation speed in one-dimensional media (string)
Consider a pulse or several successive pulses (wave) propagating with speed V in a
rope pulled (stretched) by a force of intensity F.
We call the linear mass density (µ) of a homogeneous string, with constant cross-section, which has mass (m) and length (L), the expression:
The physical meaning of µ means how much mass the string has per unit of length. Thus, a 0.5 kg/m string has, in SI, 0.5 kg of mass for every 1 meter of length. 
The speed (V) of propagation of the pulse in the string is also given by:
Where T is the intensity of the force pulling ( stretching) the rope and µ is its linear mass density.
Note that V is directly proportional to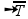 
, that is, the more stretched the string is, the greater the propagation speed of the pulse or wave in it and that V is inversely proportional to 
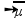, that is, the greater the linear density of the string, the lower the propagation speed of the wave in it.
Wave propagation in two-dimensional media
They can be of two types:
Circular (spherical) waves When the tip of the ruler hits the surface of the water continuously and periodically, it creates circular disturbances (circular waves) that move on the surface of the water, moving away from the point where the disturbances are generated.
The wavefront or wave surface is the geometric locus of all points that are in agreement in vibration phase , such as two crests or two troughs.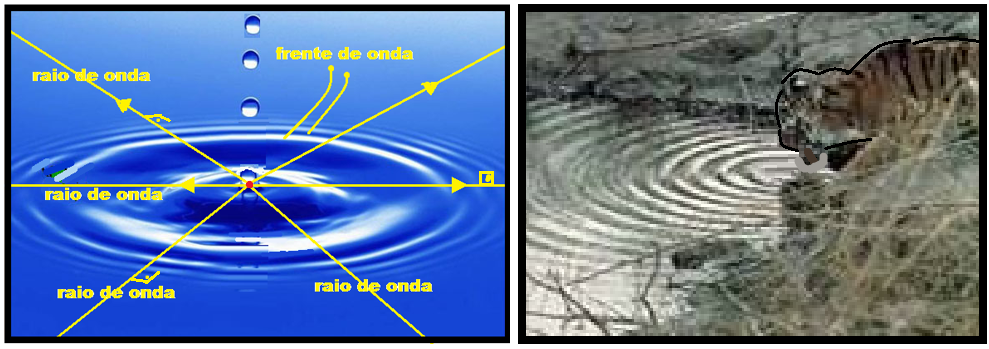
The wave ray is a straight line perpendicular to the wave fronts and which indicates the direction and sense of propagation of these waves.
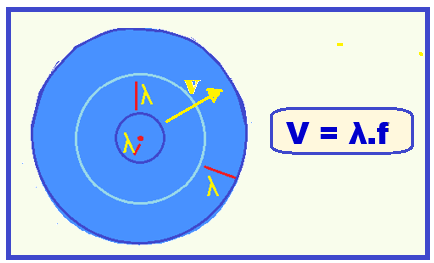
The wavelength (λ) is the distance between two consecutive wavefronts.
Plane (straight) waves
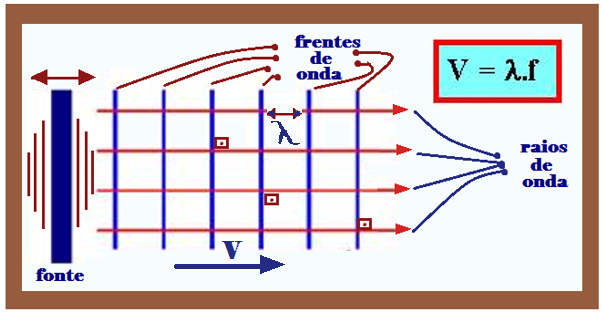
Produced by gently and continuously touching the surface of the water with a ruler (fountain) in the position indicated in the figure.
Note that the wave fronts and wave rays are parallel lines and therefore perpendicular.
Wavelength (λ) is the distance between two consecutive wavefronts (crests or troughs).
What you should know, information and tips
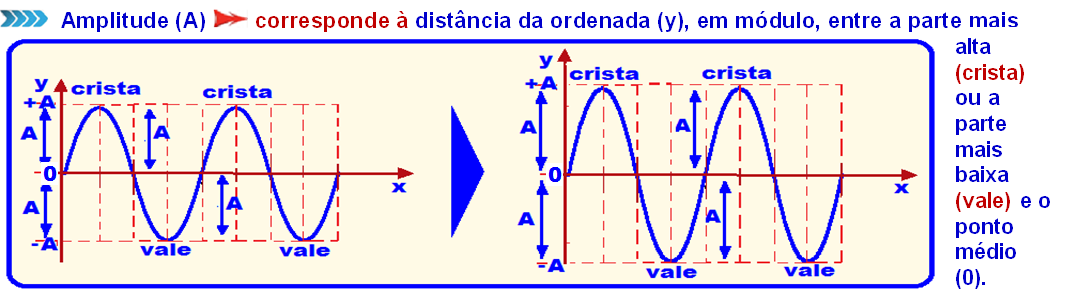
Wave amplitude (A)
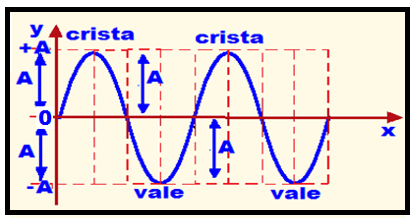
Amplitude (A) corresponds to the distance of the ordinate (Y), in module, between the highest part (crest) or the lowest part (valley) and the midpoint (0). 
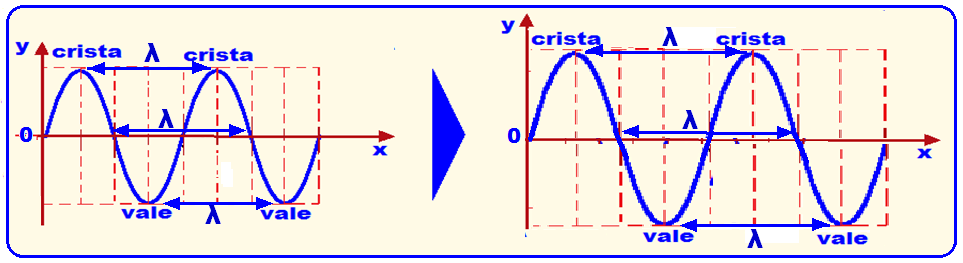
Wavelength (λ)
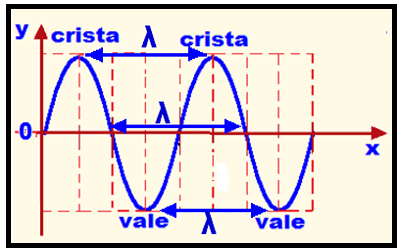
It represents the distance traveled by the wave until it starts repeating again , that is, it is the shortest distance between two consecutive points that are in phase agreement , such as the shortest distance between two crests or two troughs.
Period (T) time it takes for the wave to travel one wavelength (1λ), which is the same time it takes for any point on the wave to oscillate (come and go) completely and which is the same time it takes for the source to generate a complete wave.
Frequency (f) represents how many complete oscillations a wave makes in each unit of time, or how many complete wavelengths pass through a point on the wave in each unit of time.
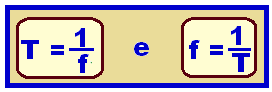
If the period T is in seconds (s) the frequency will be in hertz (Hz), which means cycles per second and the relationship between f and T is below:
Formulas
If the medium is the same, V, λ and f are also the same.
The amplitude A is not related to V, f and λ, but only to the amount of energy carried by the wave. The greater the energy, the greater the amplitude and vice versa.
Circular two-dimensional waves
Two-dimensional plane waves
Waves in three-dimensional media The wave propagates in space and in all directions. Example: Sound waves and light.
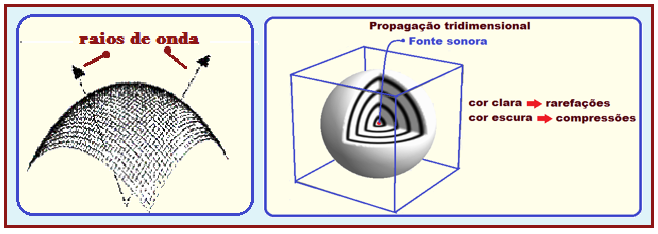
The wavefronts are spheres and the wave rays are radial and leave the disturbance source in all directions.
Interesting exercises you should check out:
01-(FUVEST-SP) In a lake the wind produces periodic waves that propagate at the speed
of 2m/s. The wavelength is 10m. Determine the period of oscillation of a boat:
a) when anchored in this lake.
b) when it moves in the opposite direction to the propagation of the waves , at a speed of 8 m/s.
Resolution:
a) With the boat anchored (stationary) V = 2 m/s λ = 10 m fundamental wave equation V = λ.f 2 = 10.f f = 0.2 Hz T = 1/f T = 1/0.2 T = 5 s.
b) As they move in opposite directions, the relative speed between the boat and the wave is V = 2 + 8 V = 10 m/s. 
The wavelength remains the same λ = 10 m = ΔS so, to travel ΔS = λ = 10 m the wave must take the time of one period Δt = T with a speed of V = 10 m/s V = ΔS/Δt
10 = 10/T T = 1 s.
Using the given expression V =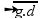 
:
In the shallowest part V 1 = 
V 1 = 5 m/s.
In the deepest part V 2 V 2 = 10 m/s.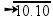 
Since, by the statement, the frequency f is the same V 1 = λ 1 .f 5 = λ 1 .f f = 5/λ 1 (I) V 2 = λ 2 .f 10 = λ 2 .f f = 10/λ 2 (II).
Equating (I) with (II) 5/ λ 1 = 10/ λ 2 5 λ 2 = 10λ 1 λ 2 = 2λ 1 .
R – B
03-(UNICAMP-SP) The GPS system (“Global Positioning System”) consists of a set of satellites in orbit around the Earth that transmit electromagnetic signals to receivers on the Earth’s surface.
The propagation speed of the signals is 300,000 km/s. For the system to work well , atmospheric absorption of this electromagnetic signal must be small .
The following figure shows the percentage of electromagnetic radiation absorbed by the atmosphere as a function of wavelength.
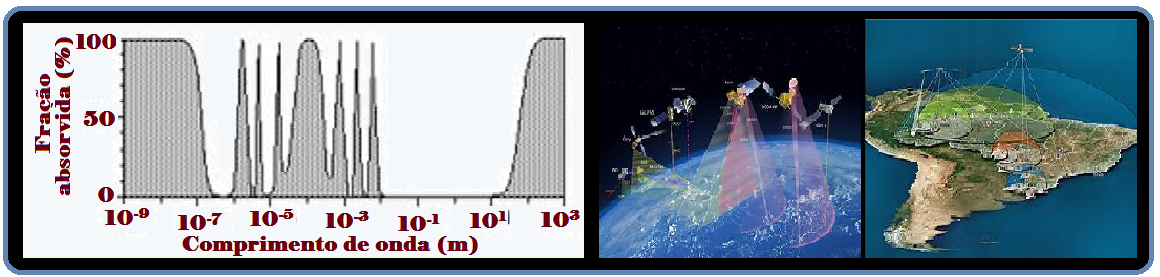
a) The frequency of the GPS signal is 1,500 MHz. What is the corresponding wavelength? What percentage of the signal is absorbed by the atmosphere?
b) One of the most important applications of the GPS system is determining the position of a certain receiver on Earth.
This determination is made by measuring the time it takes for the signal to travel from the satellite to the receiver.
What is the variation Δt in the time measurement made by the receiver that corresponds to a variation in the satellite-receiver distance of Δx = 100 m? Assume that the signal trajectory is rectilinear.
Resolution:
a) Given V = 300,000 km/s = 3.10 8 m/sef = 1,500MHz = 1500.10 6 Hz.
Applying the fundamental wave equation V = λf 3.10 8 = λ.1,500.10 6 λ = 2.0.10 -1 m.
See from the graph that for this wavelength ( λ = 2.0.10 -1 m) , the percentage (fraction) of signal absorption by the atmosphere is zero.
b) Δ x = Δ S =100m V = Δ S/ Δ t 3.10 8 = 100/ Δ t Δ t = 3.3.10 -7 s
04-(FUVEST-SP) A sensor, mounted on a Petrobrás platform, with a fixed position in relation to the seabed, records the successive positions of a small ball floating on the surface of the water , as a sea wave passes over this ball continuously.
The ball describes an approximately circular motion in the vertical plane, remaining around the same mean position , as reproduced in the sequence of recordings below , at the times indicated. The interval between recordings is shorter than the wave period.
The propagation speed of this sinusoidal wave is 1.5 m/s.
For these conditions: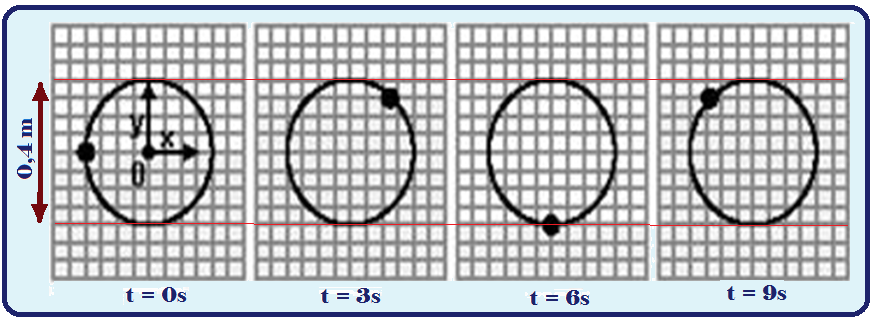
a) Determine the period T, in seconds, of this sea wave.
b) Determine the wavelength , in m, of this sea wave. 
c) Draw a diagram of the profile of this wave at time t = 14 s, as seen from the fixed platform. Indicate the appropriate values on the horizontal and vertical axes.
Resolution:
a) It is a mixed wave, as it oscillates horizontally and vertically and these oscillations in a mixed wave occur at the same time in these two directions.
Note in the figures above that the time interval of 6s corresponds to three quarters of the period T, that is, T=8s.
b) f=1/T f = (1/8) Hz V = λ.f 1.5 = λ.(1/8) λ = 12 m.
w)
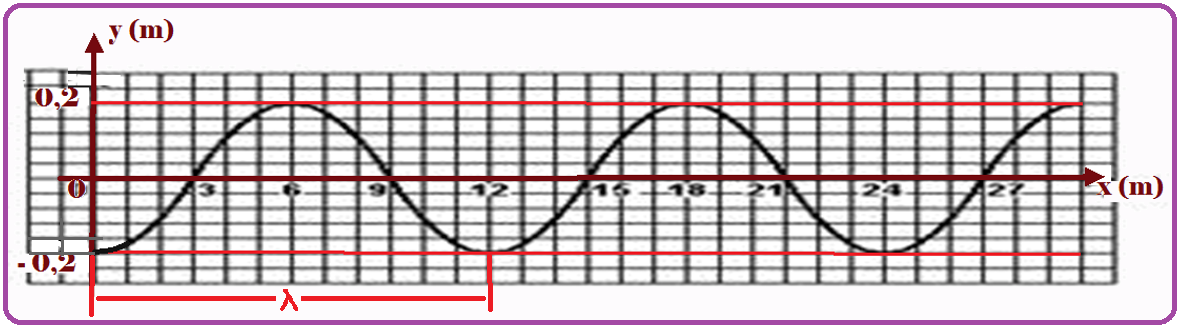
05-(UFRJ-RJ) Through a suitable device , waves are produced in an elastic medium, in such a way that the frequencies of the waves obtained are in the range of 15Hz to 60Hz. The graph shows how the wavelength (λ) varies as a function of the frequency (f).
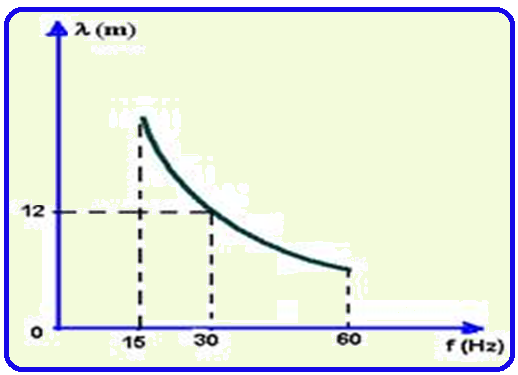
a) Calculate the shortest wavelength produced in this experiment.
b) For a wavelength of 12 m, calculate the period of the wave.
Resolution:
a) When f = 30 Hz, λ = 12 m fundamental wave equation V = .f V = 12.30
V = 360 m/s (constant-same medium).
The smallest λ occurs when f = 60 Hz (see graph) 360 = λ.60 λ minimum = 6 m.
b) When λ = 12 m, f = 30 Hz T = 1/f T = (1/30) s.
06-(FUVEST-SP) A large aquarium, with glass side walls, allows you to see a wave propagating on the surface of the water.
The figure represents the profile of such a wave at instant T o . During its passage, a buoy, in a given position, oscillates up and down and its vertical displacement (y), as a function of time, is represented in the graph
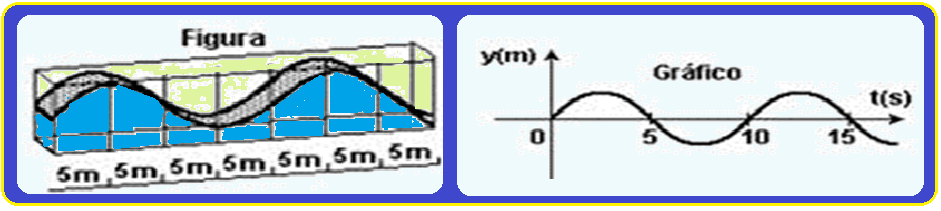
Using this information, calculate the wave propagation speed.
Resolution:
From the figure, the wavelength λ can be the distance between two successive crests λ = 20 m.
From the graph, the period T is the time interval that the wave takes to start repeating T =
10 s f = 1/T f = (1/10) Hz.
Fundamental wave equation V = λ.f V = 20.(1/10) V = 2.0 m/s.