Tubos Sonoros – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Tubos Sonoros
01- 5lλ/4=5 — λl=4m — V=λf — 340=4.f — f=85Hz
02- A
03- V=λf — 340=λ.440 — λ=0,77m — Para atingir o teto o som percorre 5m — n=5/0,77 — n=6,49 R- E
04- a) Quando f=1000Hz — I=3,0.10-6W/m2 — I=P/4pr2 — 3.10-6=4.3.102 — P=36.10-4W
b) V=λf — 340=λ.1000 — λ=0,34m — 0,34=2L — L=0,17m
05-
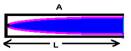
Fechado — λA/4=L — λA=4L — V=λAfA
V=4LfA — fA=V/4L — R- E
06- Tubos fechados só emitem harmônicos ímpares — fn=nV/4L — f1=1X340/4X0,5 — f1=11770Hz f3=3X340/4X0,5 — f3=510Hz R- B
07- a) 4λ/4=7 — λ=7m — 340=7f — f=48,6Hz
b) V=d/t — 340=9045/t — t=26,6s
08- a) Múltiplas reflexões de sons do próprio ambiente.
b)A freqüência predominante corresponde ao som fundamental
2λ/4=0,3 — λ=0,6m — 330=0,6f — f=550Hz
09- V=λf — λ/4=L — λ=4L — 340=4L3400 — f=0,025m R- B
10- a) área do tímpano — S=πR2=3,14.(4.10-3)2=3,14.16.10-6=50,24.10-6m2 — P=F/S — 1,01.104=F/50,24.10-6 — F≈0,507N
b)
λ/4=2,8.10-2 — λ=11,2.10-2m — V=λf — 340=11,2.10-2f — f=3.035,7Hz
11- Como fio tubo estão em ressonância a freqüência é a mesma para os dois (modo fundamental)
Fio — fn=n/2L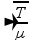
— µ=m/L — n=1 (fundamental) — f=1/2L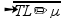
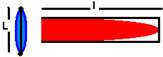
Tubo — λ/4=l — λ=4l — V=c=λf — f=c/4λ
Igualando as freqüências — f= f=1/2L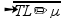 = c/4λ — T=(c/2λ)2/µL
12- Tubo fechado só tem harmônicos ímpares e sua freqüência fundamental é f1=200Hz — fn=nf1 (n=1,3,5,…) — Quando o som for de 16.000Hz, o harmônico n é de — 16.000=n.200 — n=80. Mas, 80 é par e o tubo não possui esse harmônico mas sim, o primeiro ímpar anterior que é o 79.
O primeiro harmônico é n=1. Assim, temos que determinar o número de harmônicos ímpares compreendidos entre 1 e 79 que é 38. Portanto o número de freqüências audíveis é de 40. R- D
13- f2=nV/2L — n=1 (fundamental) — f1=1.340/2.0,02 — f1=8.500Hz — n=1 (fundamental) — f10=1.340/2.10 — f10=17Hz R- A
14- I – 2λ/4=L — λ=2L — V=λf — V=2Lf — fI=V/2L
II – λ/4=L — λ=4L — V=λf — V=4Lf — fII=V/4L
III – λ/2=L — λ=2L — V=λf — V=2Lf — fIII=V/2L
R- C
15- fn=nV/2L — 1700=n.340/2.0,25 — n=2,5 — R- D — na extremidade aberta, em cima temos que ter um ventre.
16- 3λ/4=0,6 — λ=0,8m — V=λf — 340=0,8f — f=425Hz
17- A posição dos orifícios deve coicidir com nós (ausência de vibração) de uma onda sonora estacionária para que não haja entrada ou saída de ar nos mesmos e considere a freqüência mais baixa possível. (Dado: velocidade do som no ar=340m/s).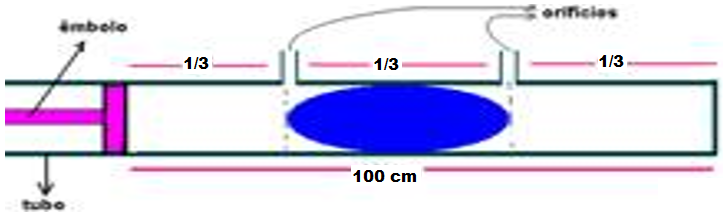
Como na posição dos orifícios temos nós e a frequência sendo a mais baixa possível teremos o seguinte formato das ondas estacionárias entre os dois nós.
λ/2=1/3 — λ=2/3m —V=λf — 340=(2/3)f — f=510Hz
18- Tubo aberto com três nós
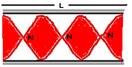
6λ/4=L — λ=2L/3 — V=λf — 340=2L/3.30 — L=17m
19- Os tubos fechados só ressoam para harmônicos ímpares — se a frequência fundamental é 500Hz, ele ressoará para: 1500Hz, 2500Hz, 3500Hz, 4500Hz, etc.
R- C
20 – Dados — L = 7 cm = 0,07 m — fmáx = 20.000 Hz — fmín = 20 Hz; v = 340 m/s — a figura mostra a configuração para o primeiro harmônico (n = 1) de um tubo aberto — o comprimento do tubo é igual a meio comprimento de onda — λ1/2=L — λ1=2L — frequência do primeiro harmônico — V= λ1.f1 — 340=2L.f1 — f1=340/2.(0,07) — f1=17.000/7 Hz — cálculo da frequência do n-ésimo harmônico — fn=nf1 — os harmônicos audíveis tem freqüências menores que 20.000Hz — fn<20.000 — nf1<20.000 — n.(17.000)/7<20.000 — n<140/17 — n<8,24 — sendo n um número inteiro — n<8 — portanto os sons audíveis estão compreendidos entre o primeiro e o oitavo harmônico e o som audível mais alto (maior frequência) é o do oitavo — f8=8f1 — f8=8.(17.000/7) — f8=19.428 Hz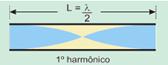
21- Considere que os três tubos estejam emitindo harmônicos de mesma ordem — a velocidade de propagação do som é mesma, pois se trata do mesmo meio, o ar — equação fundamental da ondulatória — V=λf — λ=V/f — para o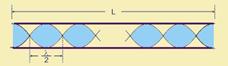
enésimo harmônico o comprimento L do tubo é dado por — L=n.( λ/2) (II) — (I) em (II) — L=n.(V/f)/2 — L=nV/2f — observe nessa expressão que o comprimento L do tubo é inversamente proporcional à frequência f do som emitido — observando a tabela fornecida — fvermelho < fazul < froxo — Lvermelho > Lazul > Lroxo — R- D
22- fn=nV/4L — f5=5V/4L — f5=5.340/4.2 — f5=212,5 Hz — R- C
23- Trata-se de um tubo aberto nas duas extremidades cujas características estão fornecidas abaixo:
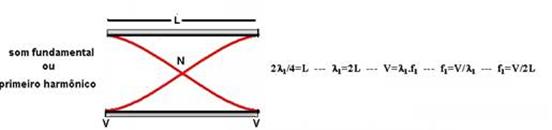
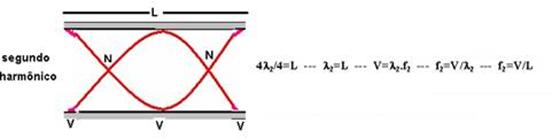
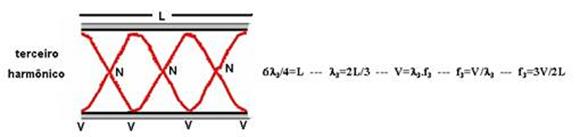
Generalizando:
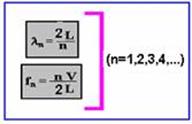
L=50cm=0,5m — V=340m/s — frequência fundamental — f1=V/2L=340/2.0,5 — f1=340Hz — R-34.
24- Inicialmente o fio se comporta como uma corda sonora vibrante, com as características a seguir:
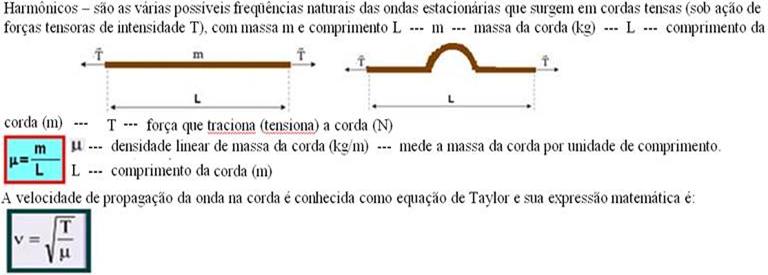
Cálculo da velocidade de propagação V da onda no fio elétrico — μ=m/L=0,001/2 — μ=0,0005kg/m=5.10-4kg/m — V=√(T/μ) — V=√(80/5.10-4) — V=√(16.104) — V=4.102=400m/s — 1o harmônico ou freqüência (som) fundamental — (dois nós e um
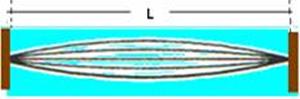
fuso) — γ1/2=L — γ1=2L — V= γ1f1 — f1=V/ γ1 — f1=V/2L — f1=400/2.2 — f1=100Hz (frequência do som fundamental emitido pelo fio elétrico) — essa frequência (100Hz) é a mesma com que a coluna de ar no buraco vibra — agora você tem um tubo sonoro fechado numa das extremidades vibrando de modo fundamental (enunciado) com velocidade do ar V=330m/s —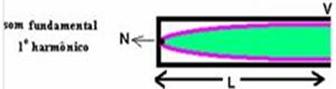 
o som fundamental num tubo fechado possui as seguintes características — γ1/4=L — γ1=4L — V= γ1.f1 — 330= γ1.100 —
γ1=3,3m — γ1=4L — 3,3=4L — L=0,825m — R- C