Tubos sonoros
Tubos Sonoros
Cálculo da velocidade de propagação do som no ar
Considere um diapasão (fonte sonora) produzindo sons sobre a extremidade aberta de um tubo de vidro de comprimento L, sendo preenchido vagarosamente com água, o que conseguimos elevando o reservatório R de água, mantendo assim os níveis de R e do tubo aberto (figura abaixo)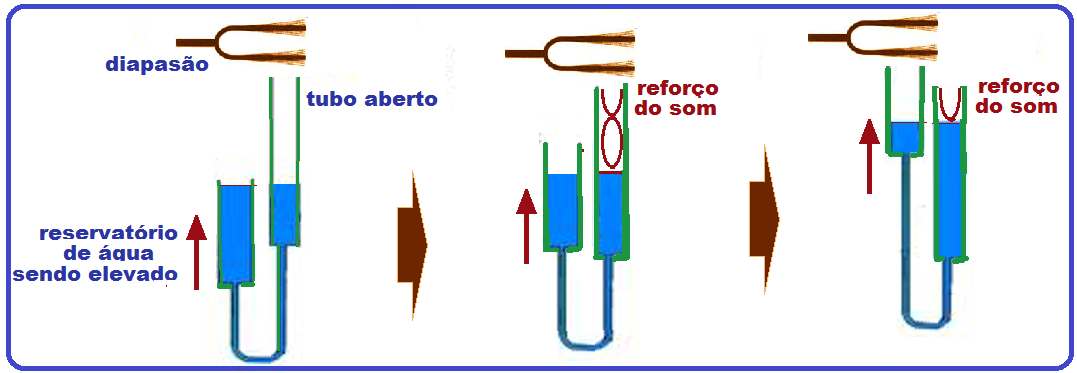
Quando o reservatório é levantado, o nível da água no tubo aberto vai subindo e assim, a intensidade do som emitido pelo diapasão é reforçado.
Isso ocorre porque, no interior do tubo, as ondas sonoras emitidas pelo diapasão sofrem interferência com as ondas refletidas na superfície da água, dando origem a ondas estacionárias que, para determinadas alturas da coluna de ar reforçará o som proveniente do diapasão.
O som terá intensidade máxima quando cada compressão, refletida pela água, volta para a abertura justamente quando a próxima está saindo do diapasão e assim elas se reforçam mutuamente.
O diapasão e a coluna de ar no interior do tubo estão em ressonância
O primeiro reforço ocorre quando a altura da coluna de água é um quarto do comprimento de onda do som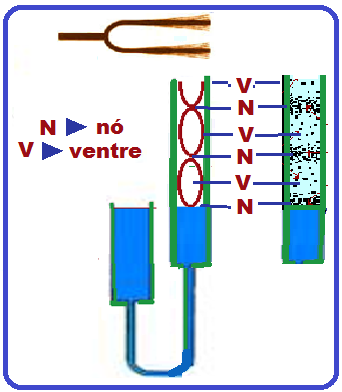 
Os sucessivos reforços sonoros ocorrem sempre que na extremidade aberta do tubo surgir um ventre (vibração máxima das partículas de ar).
A extremidade fechada é sempre um nó (vibração nula das partículas de ar).
Este processo é utilizado na determinação da velocidade de propagação do som no ar, conhecendo a freqüência f do diapasão e medindo-se a altura da coluna de ar (diferença do nível da água) entre duas intensidades máximas de som consecutivas, que nos fornece o comprimento de onda λ.
A distância d entre dois ventres (máximos) consecutivos fornece λ (d= λ /2).
Assim, conhecidos V e λ, determinamos a velocidade do som no ar através da equação fundamental da ondulatória
V = λ f.
Tubo fechado numa das extremidades
Seu princípio de funcionamento é o mesmo do processo acima onde o nível da água representa a extremidade fechada que é sempre um nó.
A extremidade aberta é sempre um ventre.
Nestes instrumentos, uma coluna de ar é posta a vibrar ao soprar-se uma das extremidades do tubo, chamada embocadura, próxima à extremidade aberta sendo que a outra extremidade é fechada.
Embocadura é a forma apropriada de usar a boca e a língua contra o bocal de um instrumento de sopro.
Na extremidade aberta um jato de ar soprado é comprimido por um calço para depois colidir contra um corte em diagonal (orifício), bem abaixo, na parede do tubo.
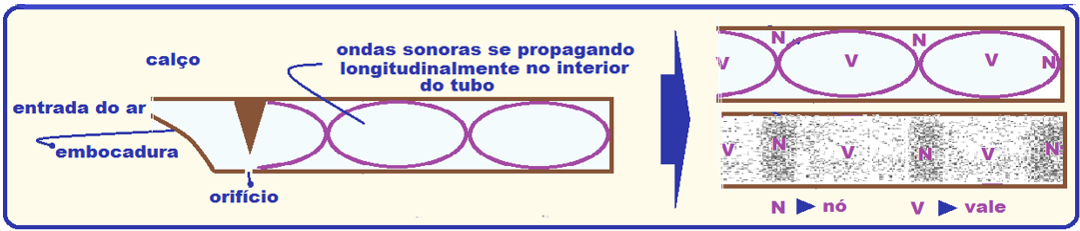Assim, o jato de ar sofre turbilhonamentos e variações de pressão que o forçam a ir, alternadamente ora para fora, ora para dentro do tubo.
Dessa maneira, a coluna gasosa interna do tubo é golpeada interminentemente, dando origem a uma onda longitudinal que se propaga no interior do tubo, com nós e ventres, provocando a emissão do som.
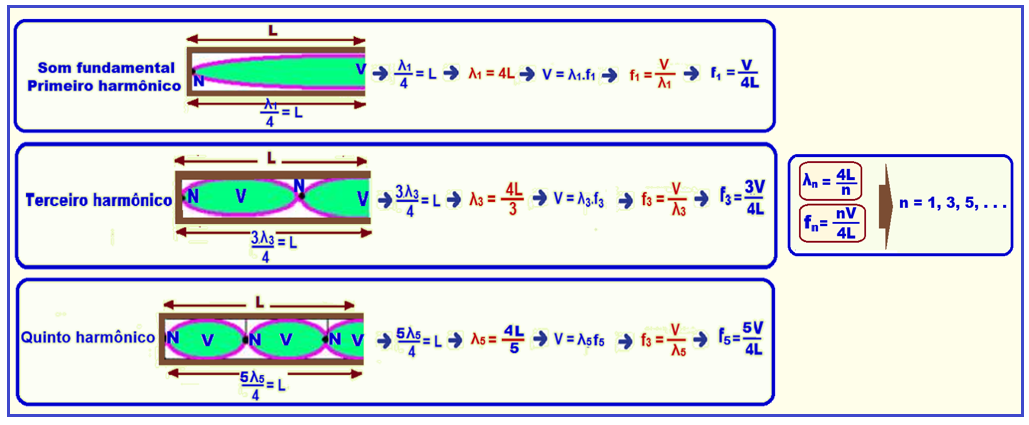
Comprimentos de onda e frequências para um tubo fechado
A seguir temos os sucessivos comprimentos de onda e freqüências para um tubo fechado numa das extremidades, de comprimento L.
V representa os ventres (pontos de vibração máxima) e N os nós (pontos de vibração nula).
Devido às configurações (simetria) das ondas em seu interior, tubos abertos só fornecem harmônicos impares.
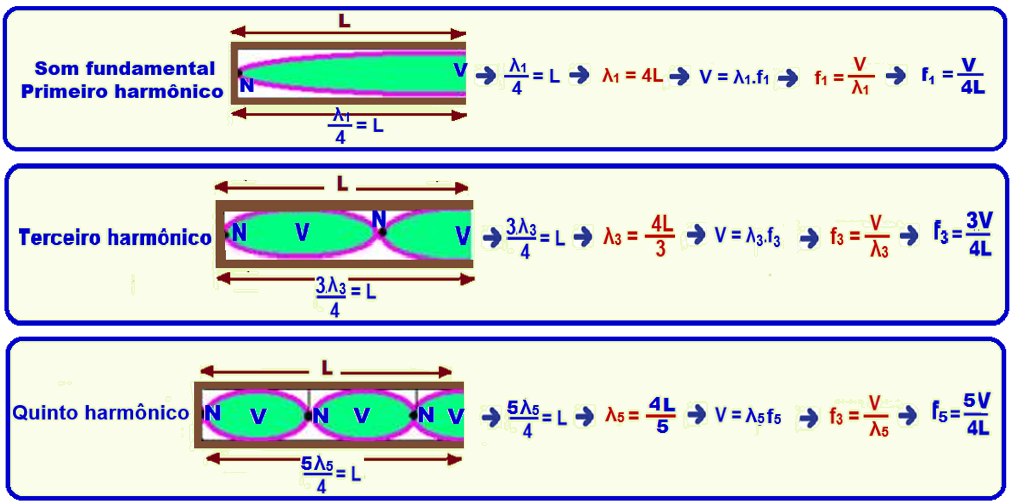
Expressões genéricas para n harmônicos:
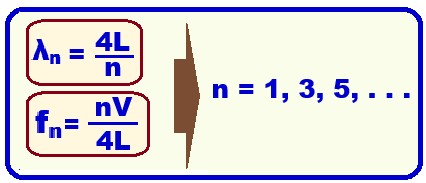
Tubo aberto nas duas extremidades
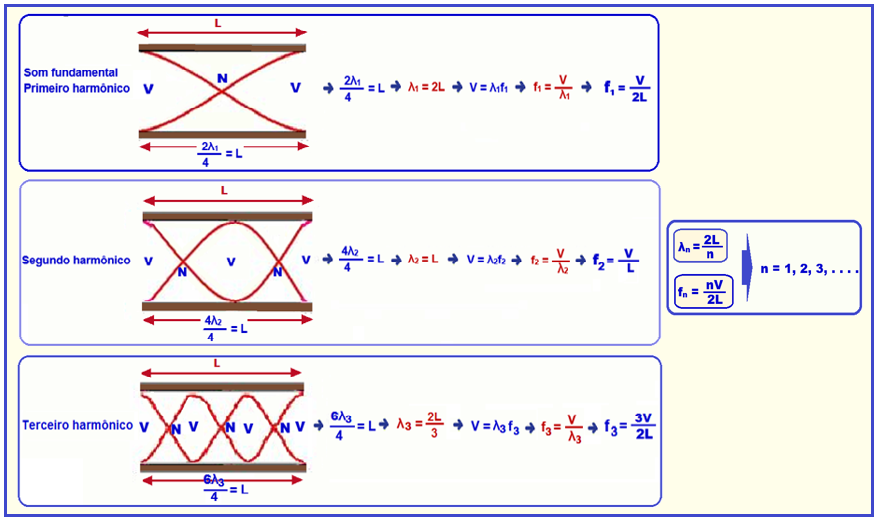
Como ambas as extremidades são abertas, em cada uma delas devemos ter ventres.
Seus harmônicos, freqüências e comprimentos de onda são os seguintes.
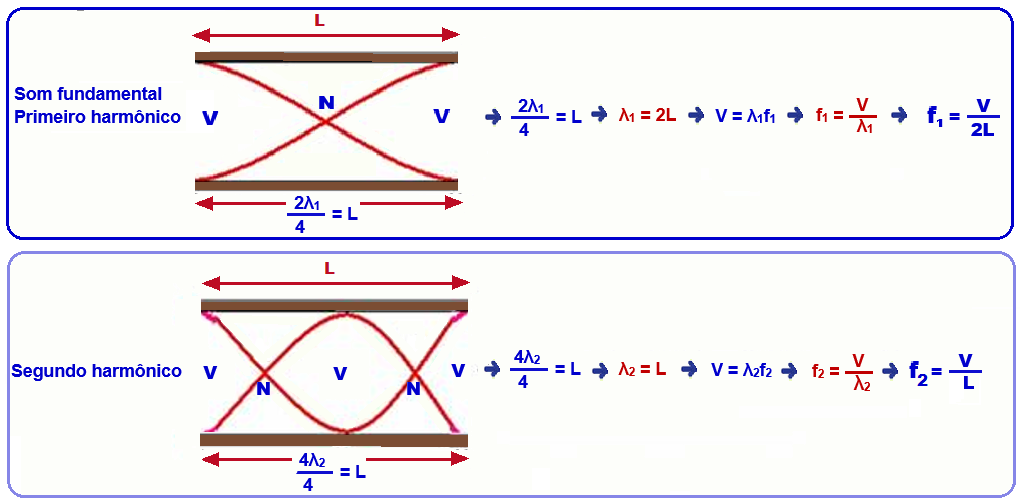
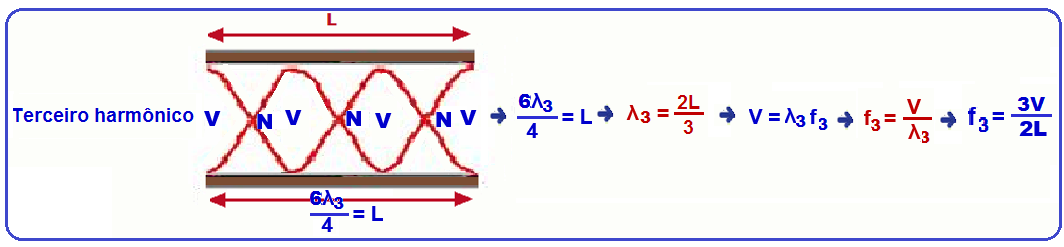
Expressões genéricas para n harmônicos:
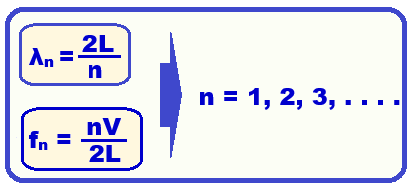
O que você deve saber, informações e dicas
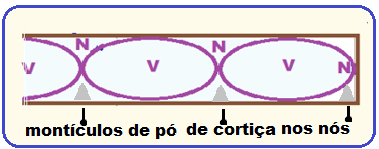
É possível visualizar através de montículos de pó de cortiça a localização de nós (região isenta de vibração, e de som) no sistema de ondas estacionárias que se estabelece como resultado da superposição da onda sonora direta e a onda sonora refletida.
Comprimentos de onda e frequências para um tubo fechado
Para produzir sons diferentes (notas diferentes) num instrumento de sopro (por exemplo, flauta doce, tubo fechado), ao mesmo tempo que o músico sobra no bocal, seus dedos tampam e destampam os orifícios distribuidos pelo corpo da flauta.
Esse comportamento provoca mudanças no comprimento da onda estacionária, que corresponde ao comprimento da coluna de ar no interior da flauta, o que influi também na variação da frequência do som obtido, produzindo maior variedade de sons (notas) emitidos.
Comprimentos de onda e frequências para um tubo aberto nas duas extremidades
Nos instrumentos mais simples como o berrante e a corneta, com ambas as extremidade abertas, o comprimento do tubo é fixo.
Mas, para se obter uma quantidade maior de freqüências, altera-se o comprimento dos tubos (abertos ou fechados).
Alguns possuem furos que podem ser tampados com os dedos (flauta simples) ou por meio de mecanismos de chaves ‘válvulas’, (saxofone, flauta transversal, etc.)
A existência de furo nos tubos (como é o caso da flauta, saxofone, clarinetes, pistão, órgãos antigos, etc), acarretará na formação de um VENTRE naqueles locais.
A velocidade de propagação da onda sonora na coluna de ar presente no interior de qualquer tubo é depende da temperatura absoluta do gás, pois V =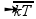 
.
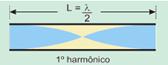
Assim, uma variação de temperatura pode alterar a afinação de um instrumento musical de sopro. Por exemplo, um aumento de temperatura, causa um aumento na velocidade de propagação do som (V é diretamente proporcional à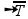 
e, assim, o tubo emitirá um harmônico fundamental de maior freqüência, portanto mais agudo.
Os instrumentos de corda também são afetados pela variação de temperatura que pode afetar o comprimento das cordas o que alterará a força tensora nas mesmas, desafinando os instrumentos.
Quando você coloca uma concha junto ao ouvido, ouve um “ruído de mar”, como muita gente diz.
Na verdade, esse som é produzido por qualquer cavidade colocada junto ao seu ouvido como, por exemplo, a sua própria mão em forma de concha ou um canudo. 
A verdadeira origem desse som, na realidade, são as múltiplas reflexões de sons do próprio meio ambiente, no interior da concha, de sua mão ou do canudo.
Assim, você está apenas ouvindo a todos os sons que estão ao seu redor.
A forma de concha funciona como um amplificador do som ambiente. É por isso que alguns anfiteatros ao ar livre têm este formato e também os auto falantes.
Encostando a concha na orelha, o ar que passar por ela vai bater e voltar nas suas superfícies internas curvadas e, esta ressonância do ar acaba criando o som que a gente percebe.
Se você quizer aprofundar seu conhecimento sobre tubos sonoros, analise atentamente as resoluções dos exercícios de números: 02; 03; 08; 10; 11; 17; 21 e 24.
Resoluções de alguns exercícios interessantes:
01–(ITA-SP) Um tubo sonoro aberto em uma das extremidades e fechado na outra apresenta uma freqüência fundamental de 200Hz.
Sabendo-se que o intervalo de freqüências audíveis é aproximadamente de 20Hz a 16.000Hz, determine o número de freqüências audíveis emitidas pelo tubo.
Resolução:
Tubo fechado só tem harmônicos ímpares a freqüência fundamental desse tubo é f1 = 200Hz.
Da teoria para tubos fechados 
fn = nf1 (n = 1,3,5,…) Quando o som for de 16.000Hz, o harmônico n é de 16.000 =n.200 n = 80.
Mas, 80 é par e o tubo não possui esse harmônico mas sim, o primeiro ímpar anterior que é o 79.
O primeiro harmônico é n = 1.
Assim, temos que determinar o número de harmônicos ímpares compreendidos entre 1 e 79 que é 38. Portanto o número de freqüências audíveis é de 40.
02-(FUVEST-SP) Um músico sopra a extremidade aberta de um tubo de 25cm de comprimento, fechado na outra extremidade, emitindo um som na freqüência f = 1.700Hz.
A velocidade do som no ar nas condições do experimento é V=340m/s.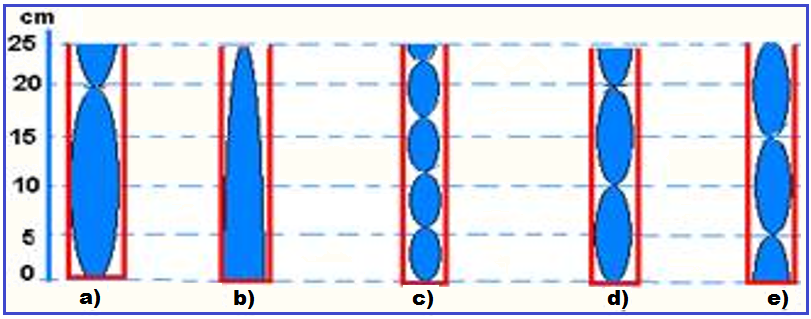 
Dos diagramas abaixo, aquele que melhor representa a amplitude de deslocamento da onda sonora estacionária no tubo pelo sopro do músico, é:
Resolução:
Cálculo de n quando a frequência for de f = 1700 Hz para o tubo fechado numa extremidade de comprimento L = 25 cm = 0,25 m fn = nV/2L 1700 = n.340/2.0,25 n = 2,5.
Assim, você terá 3 nós (um na extremidade fechada) e, na extremidade aberta, em cima deverá ter um ventre.
R- D
03- (UDESC-SC) Dois tubos sonoros de um órgão têm o mesmo comprimento, um deles é aberto e o outro fechado. O tubo fechado emite o som
fundamental de 500 Hz à temperatura de 20oC e à pressão atmosférica normal.
Dentre as frequências abaixo, indique a que esse tubo não é capaz de emitir.
a) 1500 Hz
b) 4500 Hz
c) 1000 Hz
d) 2500 Hz
e) 3500 Hz
Resolução:
Os tubos fechados só ressoam para harmônicos ímpares.
Se a frequência fundamental (n=1) é 500Hz, ele ressoará para: (n = 3 3×500 = 1500 Hz), (n = 5 5×500 = 2500Hz), (n = 7 7×500 = 3500 Hz), (n = 9 9×500 = 4500 Hz), etc.
R- C
04-(ITA-SP)
O tubo mais curto de um órgão típico de tubos tem um comprimento de aproximadamente 7 cm. Qual é o
harmônico mais alto na faixa audível, considerada como estando entre 20 Hz e 20.000 Hz, de um tubo deste comprimento aberto nas duas extremidades?
Resolução:
São dados L = 7 cm = 0,07 m fmáx = 20.000 Hz fmín = 20 Hz v = 340 m/s.
A figura mostra a configuração para o primeiro harmônico (n = 1) de um tubo aberto nas duas extremidades o comprimento do tubo (L) é igual a meio comprimento de onda (λ1) λ1/2 = L λ1 = 2L. Frequência do primeiro harmônico V = λ1.f1 340 = 2L.f1 f1 =340/2.(0,07) 
f1 = 17.000/7 Hz.
Expressão da frequência do n-ésimo harmônico fn = nf1.
Os harmônicos audíveis tem freqüências menores que 20.000Hz fn < 20.000 nf1 < 20 000
n.(17.000)/7 < 20.000 n < 140/17 n < 8,24 ( sendo n um número inteiro n < 8).
Portanto os sons audíveis estão compreendidos entre o primeiro e o oitavo harmônico e o som audível mais alto (maior frequência) é o do oitavo harmônico.
f8 = 8f1 f8=8.(17.000/7) f8 =19 428 Hz.