Ondas Sonoras – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Ondas Sonoras
01- a) V=ΔS/Δt — 340=ΔS/3 — ΔS=1020m (ida e volta) — ΔS=510m
b) V=ΔS/Δt — 340=ΔS/0,1 — ΔS=34m (ida e volta) — ΔS=17m
02- V=ΔS/Δt — 350=ΔS/0,100 — ΔS=35m (ida e volta) — ΔS=35/2=17,5m
03- E
04- T = 8.10-3s — T=1/f — 8.10-3=1/f — f=125Hz
05– C
06- C
07- E
08- Como a freqüência (f) dobra e o período (T) é o inverso da freqüência, ele será reduzido à metade, o que ocorre na figura C.
Ou, sendo V= λf — se f dobrar, sendo V constante (mesmo meio), o comprimento de onda λ deverá ser reduzido à metade, passando de 40cm para 20cm.
09- a) V=ΔS/Δt — 1540=0,2/Δt — Δt=1,3.10-4s
b) V=ΔS/Δt — 1540=ΔS/2,5.10-5 — ΔS=3,85cm — até o ponto A — d=10-3,85 — d=6,15cm
10- V= λf — 340= λ1000 — λ =0,34m=34cm R- D
11- a 0oC — V0=330m/s a 40oC — V=330+0,59X40 — V=353,6m/s
a razão V/Vo é 353,6/330=1,07 e é linear (reta) R- A
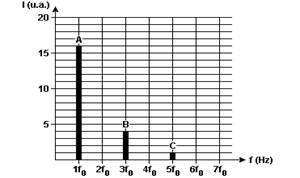
12- a) A — λA=1,5m
B — λB=0,5m
C — λC=0,3m
b) λS=1,6-0,1=1,5m
c) a velocidade de propagação é a mesma para as três ondas A, B e C e vale 340m/s.
cálculo da frequência de cada uma — V=λf — f=V/λ
fA=V/λA — fA=340/1,5=226,7Hz
fB=V/λB — fB=340/0,5=680Hz
fC=V/λC — fC=340/0,3=1133.3Hz
– O menor comprimento de onda que o exercício manda chamar de fo é o da A — fA=fo=226,7Hz
Segundo o enunciado λ=A2 — λA=42 — λA=16 ua
– A maior freqüência é a da onda C e vale — fC/fo=1133,3/226,7=5 — fC=5fo
λC=(AC)2 — λC=12 — λC=1 ua
Colocando-os no gráfico, temos:
13- a) V=ΔS/Δt — 1400=ΔS/0,8 — ΔS=1120m (ida e volta) — ΔS=560m
b) a frequência no ar e na água é a mesma (mesma fonte) e vale f=4.104Hz
ar — V=λf — 370=λar.4.104 — λar=9,25.10-3m
água — V=λagua.f — 1400= λagua.4.104 — λagua=35.10-3
λar/λagua=9,25.10-3/35.10-3=0,264
14- a) 2001, Uma odisséia no espaço, pois o som não se propaga no vácuo.
b) Os dois estão corretos, pois a luz se propaga no vácuo
15- Quando, novamente, som e imagem forem simultâneos, a pessoa estará ouvindo o som da pancada anterior, que estará percorrendo a distância de 172m em 0,5s.
V=ΔS/Δt — V=172/0,5 — V=344m/s
16- a) distância até o paredão d
emerso — Var=2d/0,731 — imerso — Vágua=2d/0,170 Vágua/Var=2d/0,170X0,731/2d=4,3
b) a frequência f é a mesma (mesma fonte)
Vágua/Var=λágua.f/λar.f — 4,3=λáguaλlar
17- Período T=20.10-6s — f=1/T — f=1/20.10-6 — f=5.104Hz — f=50.000Hz — R- D
18- Tempo que o som demora para percorrer ΔS=3X340=1.020m, com V=340m/s — V=ΔS/Δt — 340=1020/Δt — Δt=3s.
Nesse tempo, o corredor com V=10m/s, percorreu — V=ΔS/Δt — 10=ΔS/3 — ΔS=AX=30m
19- V=ΔS/Δt — 1520=ΔS/3 — ΔS=4.560m
20- Para anular o som original, o computador deve enviar ondas que provoqueminterferência destrutiva. R- A
21- O som chega ao observador com atraso e som e imagem serão simultâneos quando o atraso for um múltiplo do período das marteladas, ou seja, a cada 0,9s, 1,8s, 2,7s, etc. No caso, a menor distância ocorre com um atraso de Δt=0,9s.
V=ΔS/Δt — 330=ΔS/0,9 — ΔS=297m
22- Calculo do instante em que o alto-falante está emitindo o som de freqüência F1=1.080Hz
F(t)=1000+200t — 1080=1000+200t — t=0,4s
Calculo do intervalo de tempo que qualquer som emitido pela fonte demora para chegar à pessoa P que está a Δ=34m da fonte.
V=ΔS/Δt — 340=34/Dt — Δt=0,1s
O som que a pessoa percebe tem um atraso de 0,1s em relação ao som emitido pela fonte. Assim, t2=0,4s – 0,1s=0,3s
F(2)=1000+200.0,3 — F2=1.060Hz
23- através do trilho — V=ΔS/Δt — 3400=L/t1 — t1=L/3400
– pelo ar — V=ΔS/Δt — 340=L/t2 — t2=L/340
Como a viagem pelo ar demora mais, temos que t2 – t1=0,18 — L/340-L/3400=0,18 — L=68m
24-
As ondas eletromagnéticas emitidas na região litorânea do Brasil atingem a região amazônica após sofrer reflexão total na ionosfera — R- A
25- A distância percorrida pelo som até que Patrícia ouça o eco de sua voz direta é igual a 2d (ida e volta) — v=∆S/∆t — v = 2d/∆t — 340=2d/0,4 — d=136/2 — d=68m — R- B
26- 01. Falsa — a frequência de uma onda não se altera quando ela reflete ou refrata, permanecendo constante, igual a frequência com que foi emitida pela fonte.
02. Correta — trata-se da afirma a 1ª lei da reflexão.
04. Correta — desde que a onda seja mecânica — as ondas eletromagnéticas também são transversais, mas não provocam vibrações nas partículas do meio — a vibração dá-se nas intensidades dos campos elétrico e magnético que se propagam pelo meio.
08. Correta — a velocidade de uma onda depende das condições do meio — por exemplo, no ar, a velocidade do som depende da umidade e da temperatura e na água depende da profundidade.
R- (02 + 04 + 08) = 14
27- Como o som vai e volta ele percorre ∆S=2h — V=∆S/∆t —1,6.103 = 2h/0,8 — h=1,6.103.0,4 — h=640m — equação fundamental da ondulatória — V=λ.f — 1,6.103= λ.4.104 — λ=1,6.103/4.104 — λ=0,4.10-1=4.10-2m —
R- A.
28- Raio, relâmpago e trovão são fenômenos atmosféricos que ocorrem antes ou durante tempestades, causados por descargas elétricas entre nuvens ( relâmpago ) ou entre uma nuvem e o solo ( raio ), acompanhados de um estrondo ( trovão ) — o raio ocorre quando uma nuvem, carregada de eletricidade estática, atinge um potencial eletrostático tão elevado que a camada de ar existente entre ela e o solo deixa de ser isolante, tornando-se condutor, permitindo a movimentação das cargas elétricas até o solo — com o relâmpago ocorre a mesma coisa só que é entre as nuvens — essas descargas elétricas produzem uma grande luminosidade devido ao aquecimento do ar, que pode ser vista bem distante — o trovão é o som que acompanha a violenta expansão do ar quando é rapidamente aquecido — devido à diferença de velocidades da luz e do som (luz, 3.108m/s e som, 340m/s), quando o raio ou relâmpago ocorre a grande distância do local de observação, o trovão é ouvido alguns segundos depois do clarão — R- E.
29- Pressão=força/área — Pr=F/S — densidade=massa/volume — ρ=m/Vo — Vo=S.ℓ — ρ=m/S.ℓ — Pr=F/S —F=m.a — Pr=m.a/S — multiplicando o numerador e denominador por ℓ — Pr=m.a.ℓ/S.ℓ — Pr=m.a.ℓ/Vo — mas, m/Vo=densidade=ρ — Pr=ρ.a.ℓ — aceleração a=ve/t — Pr= ρ.(Ve/t).ℓ — Ve= ℓ/t — Pr=ρ.Ve.Ve — Pr=ρ.Ve2 —
Ve=√(Pr/ρ) ou Ve=(Pr/ρ)1/2 — R- C.
