Standing Waves – EN
Standing Waves
Formation of standing waves
We obtain standing waves by superposing two identical waves, of the same amplitude, same frequency, same wavelength and that move in the same direction and opposite directions.
Consider a string fixed at one end and a source producing periodic waves at the other.
which, upon reaching the fixed end, undergo reflection and return.
Thus, the incident and reflected waves superimpose , creating standing waves.
To understand how standing waves arise , carefully observe the sequences of figures below, where, in all of them, at the same time , in the two figures on the left, we have waves moving in opposite directions and, in the figure on the right, their superposition, at the same time.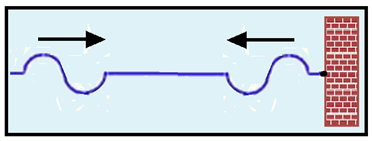
The time interval between one figure and another is a quarter of a period (T/4), that is, between each interval the wave traveled a quarter of a wavelength.
At time t = 0, the two waves are exactly superimposed and the wave resulting from this superposition has amplitude 2A. (constructive interference).
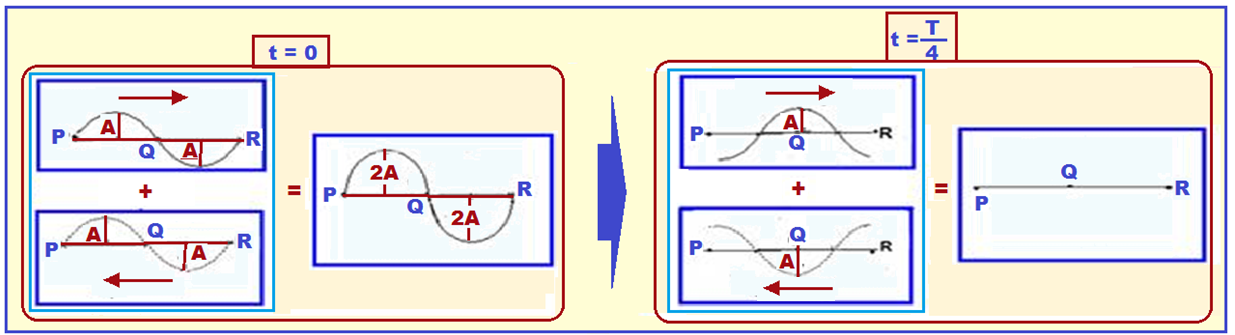
At time t = T/4, each of them has moved λ/4 and their configurations are shown in the two figures on the left. Note, in the figure on the right, that all the points of these waves cancel each other out (destructive interference).
At time t = T/2, the resulting wave has amplitude 2A.
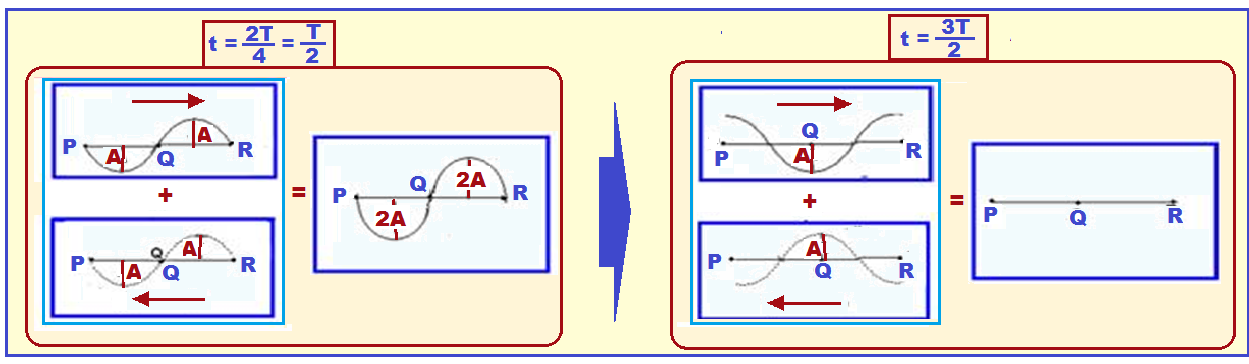
At time t = 3T/2 these waves cancel each other out again.
At instant t=T , these waves returned to the initial situation and from then on the repetition begins.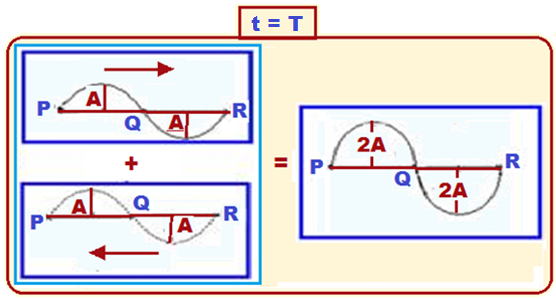
Note that at all instants, points P, Q and R of the resulting wave did not move. These points, which are always fixed, are called nodes and are in destructive interference.
Also note that at all instants, all points between P and Q and between Q and
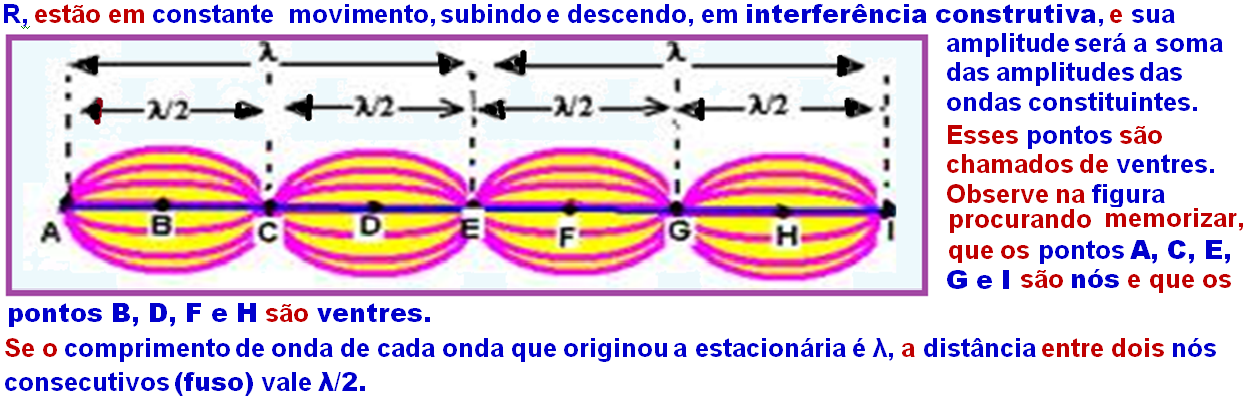
Each of these amplitudes is twice the amplitudes of the constituent waves.
Since the nodes are at rest, there can be no passage of energy through them , meaning that there is no energy transport in a stationary rope .
Thus, standing waves are not propagating waves, but rather the different ways in which a string, membrane, etc. vibrates.
Sound interference
It occurs when two or more sound waves overlap at the same point.
Let us suppose two sound waves of slightly different frequencies, one of f A = 100 Hz and the other of f B = 110 Hz.
Then you will hear a loud sound (constructive interference) and then a soft sound (destructive interference) and so on. This phenomenon is called a beat (figure).
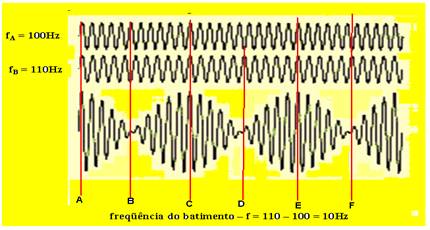
Note that the resulting wave presents points where the amplitude is maximum (loud sounds, constructive interference) as in points A, C and E, it decreases and practically disappears or is cancelled out (destructive interference) as in points B, D and F.
The beat frequency is defined as f beat = f major – f minor .
The phenomenon of beating is often used in the tuning of musical instruments.
If the frequencies of the sharpening source and the instrument are different, the beat is heard.
The frequency of the beat decreases as the instrument is tuned , and when it disappears, the instrument is in tune.

What you should know, information and tips





![]()

![]()
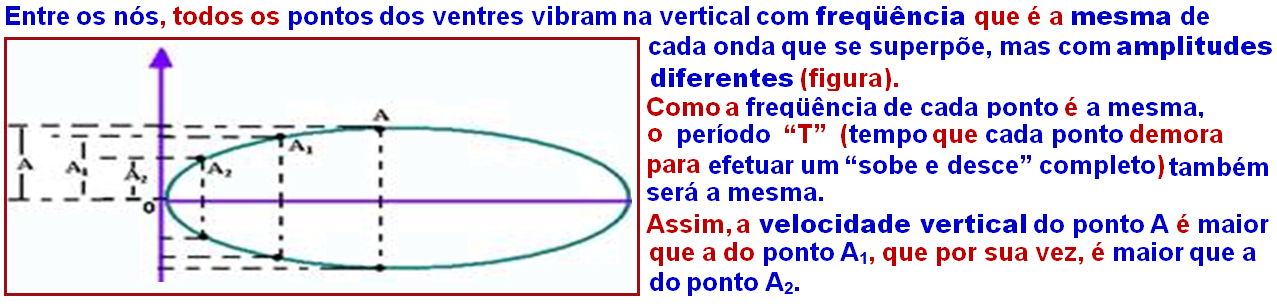
Each of the amplitudes of the standing wave is twice the amplitudes of the constituent waves.
![]()
Since the nodes are at rest, there can be no passage of energy through them, meaning that there is no energy transport in a standing wave.
Thus, standing waves are not propagating waves , but rather the different ways in which a string, membrane, etc. vibrates.
![]()
The beat frequency is defined as f beat = f major – f minor .
![]()
The phenomenon of beating is often used in the tuning of musical instruments.
If the frequencies of the sharpening source and the instrument are different, the beat is heard.
The frequency of the beat decreases as the instrument is tuned , and when it disappears, the instrument is in tune.
![]()
Formulas
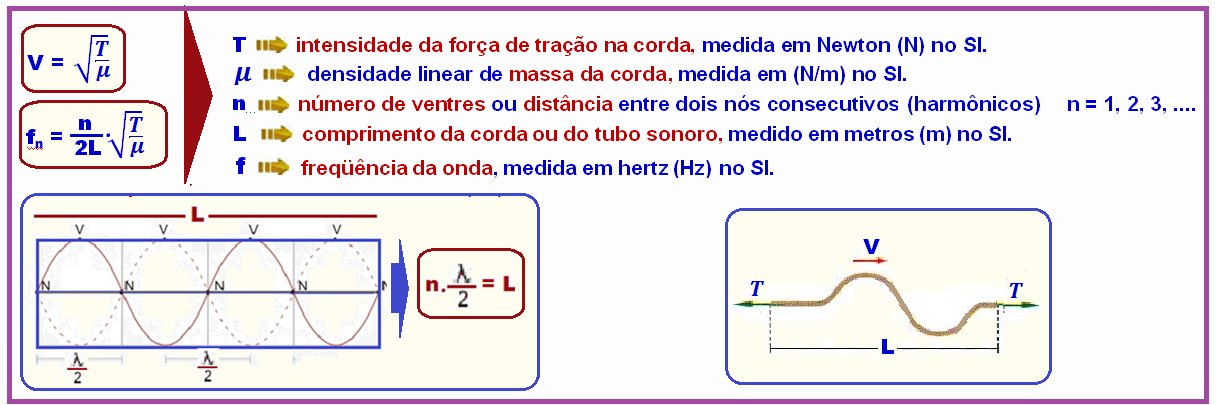
![]()
Some interesting exercises in which you might want to analyze the resolutions:

02- (UFMS) The figure shows standing waves in a string of length 45 cm, with linear mass density μ = 6.2 g/m, with both ends fixed, and which is vibrating at 450 Hz.
Give as your answer the sum of the numbers corresponding to the correct statements.
It is correct to state that:
(01) all points of the string vibrate with the same amplitude.
(02) all points of the string vibrate at the same frequency.
(04) the wavelength on the string is 90 cm.
(08) the wave propagation speed in the rope is 135 m/s.
(16) the tension force on the rope is approximately 113N .
Resolution:
(01) Wrong. The movement of each point of the standing wave is only vertical and check in the figure below that points A, A1 and A2 have different amplitudes in their complete “up and down”.

(02) Correct. This frequency of 450Hz is the frequency of the waves that superimpose and is the same for all points of the string that vibrate.
(04) Wrong. 3λ/2 = 45 λ = 30 cm. ![]()
(08) Correct. V = λf V = 30,450 = 13,500 cm/s = 135 m/s. ![]()
(16) Correct. V=√(F/μ) 135 = √(F/6.2.10 -3 ) (135) 2 = (F/6.2.10 -3 ) 2 18.225 = F/0.0062 ![]()
![]()
![]()
![]()
F = 112.995 N.
Sum = (02 + 08 +16) = 26

Resolution:
Applying the fundamental wave equation to:
City radio V = λ c .f c . ![]()
Pirate radio V = λ p .f p . ![]()
As the speed (V) of wave propagation is the same, as it is the same propagation medium (air), and the frequencies (f), according to the statement, are the same , the wavelengths (λ) will also be the same.
R- And

Resolution:
Point 2 on the string is a node of the standing wave and remains fixed .
Points 1 and 3 have zero speed at the upper and lower ends and maximum speeds when they pass through the center (where these points are), but they have speeds in opposite directions, that is, while one is going up the other will be going down.
R-D.

Resolution:
Observe in the figures below the standing waves formed in each case:
First figure λ 1 /2 = L γ 1 = 2L V 1 = γ 1 .f 1 V 1 = 2L.f 1 (I). ![]()
![]()
![]()
![]()
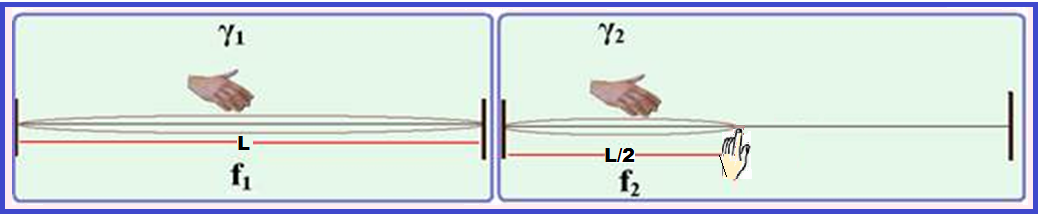
Second figure γ 2 /2 = L/2 γ 2 = L V 2 = γ 2 .f 2 V 2 = Lf 2 (II). ![]()
![]()
![]()
![]()
Since the propagation speed in each case is the same (same medium, air) ![]() V 1 = V 2 I = II 2Lf 1 = Lf 2 — 2,220 = f 2 f 2 = 440 Hz.
V 1 = V 2 I = II 2Lf 1 = Lf 2 — 2,220 = f 2 f 2 = 440 Hz. ![]()
![]()
![]()
A- A
