Efeito Doppler – Resolução

Resolução comentada das questões de vestibulares sobre

Efeito Doppler

 

01-

I – Errada  —  mais agudo  —  ambulância se aproximando  —  recebe mais frentes de onda.

II – Correta  —  a distância entre o observador e a fonte é sempre a mesma (raio da circunferência).

III – Errada  —  mais grave  —  ambulância se afastando  —  recebe menos frentes de onda.

IV – Errada  —  vide I, II e III acima.

R – C

02- (1) Falsa  —  a freqüência da fonte é a mesma

(2) Falsa

(3) Verdadeira  —  a distância fonte-observador é a mesma

(4) Falsa  —  vale também para a luz que não necessita de um meio material para se propagar.

F F V F

03- D         

04- A         

05- C          

06- D 

07- Apenas a componente horizontal de U, U_x influi no movimento, pois as frentes de onda são planas (vide figura)

U_x=Ucos60^o  —  U_x=6,6.0,5  —  U_x=3,3m/s  —  cálculo da freqüência da fonte  —  V=lf  —  330=0,165f  —  f=2.000Hz

f_a=2000(330-3,3)/330  —  f=653.400/330  —  f=1.980Hz  R- B

08-

a) Maior. À medida que a pessoa se aproxima da fonte, ele observa um aumento do número de frentes de onda passando por ele por unidade de tempo em relação a situação em que a pessoa se encontra parada, implicando num aumento da freqüência.

b) Se aproximando  —  f₁=735(343+V)/343  —  f₁=735 + 2,1V

 Se afastando  —  f₂=735(343-V)/343  —  f₂=735-2,1V

 Δf=f₁-f₂  —  78=735+2,1V – (735-2,1V)  —  78=735+2,1V -735 +2,1V  — V=18,6m/s

09- 

– f₁  —  a fonte se afasta do observador que está em repouso

. f₁=f.V/(V+V_f)  —  f₁=400.340/(340+1,7)  —  f₁=136.000/341,7  —   f₁=398Hz

– f₂  —  som se aproxima do observador que está parado

F₂=V/(V-V_f)  —  f₂=400.340/(340-1,7)  —  f₂=136.000/338,3  —  f₂=402Hz

– a frequência de batimento, por definição, é fornecida por f_B=f_maior – f_menor  —  f_B=402-398  —  f_B=4Hz   R- C

10-  V_o=0  —  V_f=?  —  f_a=436Hz  —  f=440Hz

 Cálculo de V_f (velocidade com que o diapasão chega ao solo)  —  Dopper  —   f_a=f.V/V+V_f)  —  436=440.330/(330+V_f)  —  436/440=330/330+V_f  —  145.200=143.880 + 436V_f  —  V_f≈3m/s

Queda livre  —  aplicando Torricelli com V_o=0 e a=g=10m/s²  —  V²=V_o² + 2.a.DS  —  3²=0² + 2.10.h  —  h≈0,45m

 

11- V_o=80/3,6 m/s  —  V_f=0  —   f=700Hz  —  V=340m/s  —  f_a=f(V+V_o)/V  —  f_a=700(340+80/3,6)/340  —  f_a=700(1 + 80/3,6.340) — f_a=700 + 56.000/1.224  —  f_a≈744Hz  R- B

12- V_A=V_B=125/3,6=34,7m/s  —  as freqüências aparentes são iguais, ou seja, f_aA=f_aB)

Ambulância A – está se afastando do observador parado  —  f_aA=f_A.V_som/(V_som+V_A) (I)

Ambulância B – está se aproximando do observador parado  —  f_aB=f_B..V_som/(V_som-V_B) (II)

Dividindo membro a membro I por II:

F_aA/f_aB = f_A.340/340+34,7 X 340-34,7/f_B.340  —  1=305,3.f_A / 374,7.f_B  —  f_A/f_B=374,7/305,3  —  f_A/f_B=1,23

13- Automóvel se aproximando do observador parado  —  f_a=f.V/(V-V_f)  —  284=f.330/(330-V_f)  —  284/f=330/330-V_f   I

Automóvel se afastando do observador parado  —  f_a=f.V/(V+V_f)  —  266/f=330/330+V_f   II 

Dividindo I por II:

284/f X f/266=330/330-Vf X 330+V_f/330  —  284/266=330+V_f/330-V_f  —  266(330+V_f) = 284(330-V_f)

87.780 + 266V_f = 93.720-284V_f  —  550V_f = 5.940  —  V_f = 10,8m/s  —  R- A

14- A

15- Observe o esquema da figura abaixo  —  no instante t = 0 a jovem (ouvinte ou observador) está na posição mostrada na figura  —   nesse ponto, a frequência ouvida (f) é igual a frequência da sirene (f_o) tal que f/f_o=1  — A partir desse instante, atéT/2, há afastamento relativo entre a jovem e a sirene, de modo que a frequência ouvida por ela é menor que a frequência emitida pela sirene f/f_o<1  —  quando t =T/2, ela volta a ouvir a frequência emitida pela fonte  —  De T/2 até T, ocorre aproximação relativa entre a jovem e a sirene e ela passa a perceber uma frequência maior que a emitida pela sirene f/f_o>1  —  as velocidades máximas de afastamento e de aproximação ocorrem em t = T/4 e em t =3T/4, instantes em f/f_oatinge valores mínimo e máximo, respectivamente  —  R- A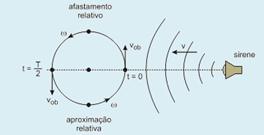

16- 

(01) Errada  —  a velocidade de propagação de uma onda só depende da característica da própria onda e das condições do meio.

(02) Errada —   velocidade de propagação da onda independe da velocidade da fonte.

(04) Correta  —  quando a onda sonora se reflete na parede, esta funciona como fonte  —  como o morcego está se aproximando da fonte, ocorre o efeito Doppler e ele detecta um som mais agudo que o emitido, ou seja, de maior frequência.

(08) Correta  —  o meio é o mesmo.

(16) Errada  —  como já especificado, chama-se efeito Doppler. 

 R- (04 + 08)=12

17- a) Dados  —  v_som = v = 340 m/s  —   λ = 50 cm = 0,5 m  —  equação fundamental da ondulatória  —  v= λf  —  340=0,5f  —  f=680Hz

b e c) Dados  —   v_fonte = 0; v_ouvinte = 72 km/h = 20 m/s  —  a frequência aparente (f_ap) percebida pelo motorista da ambulância (ouvinte) é dada pela expressão do efeito Doppler  —  f_ap={(v_som + v_ouvinte)/(V_som + V_fonte) }.f  —  colocando os valores  — f_ap=(340 + 20)/(340 + 0).680  —  f_ap=720Hz  —  esse valor significa que o motorista recebe 720 frentes de onda por segundo  — em três segundos, a quantidade de frentes de ondas (N) recebidas é  —  N = 3 (720)  —  N = 2.160.

18- A questão refere-se ao efeito Doppler, que dá a frequência aparente percebida por um ouvinte quando entre ele e a fonte ocorre movimento relativo. Quando há aproximação relativa, a frequência aparente é maior que a emitida pela fonte e, menor, quando há afastamento relativo.

a) Errada. A velocidade do som num fluido depende da velocidade desse fluido. A frequência aparente para o golfinho é maior que 9,74 kHz, como se a baleia se movesse com a mesma velocidade da correnteza em águas paradas.

b) Errada. Nada se pode afirmar, pois não foi fornecida a velocidade do som na água.

c) Correta. Haveria aproximação relativa entre o golfinho e a baleia. Assim, a frequência percebida pelo golfinho seria maior que a frequência emitida pela baleia.

d) Errada. O golfinho emitirá som na mesma frequência recebida.   

R- C

19- V_m=72km/h=20m/s  —  conforme o enunciado, quando o carro se aproxima do radar, a frequência da onda refletida

(f) é maior que a da onda emitida (f_o)  —  o que implica que a diferença ∆f = f – f_o deve ser maior que zero  —  para isso, você deve escolher o valor positivo para a velocidade média V_m  na equação ∆f = f – f_o ±(V_m/c).f_o  —  substituindo  —   ∆f=+ (20/3.10⁸).2,4.10¹⁰  —   ∆f= + 1.600 Hz  —  R- A

20- Equação do efeito Doppler  —  f/f_o=(V – V_o)/(V – V_f)  —  225/235=(340 – 0)/(340 – V)  —  V=-15,1m/s  —  supondo a velocidade da pessoa nula quando a mola estiver esticada em 20m  —  E_mf = E_mi  —  mgh_o=kx²/2  —  80.10.20=k.4²/2  —  k=2.000N/m  —  condição em que a corda não está esticada  —  E_mi=E_mf  —  mgh=mV²/2  —  10h=(-15,1)²/2  —  h=11,4m  — 

Condição em que a corda se encontra tracionada  —  E_mi=E_mf  —  mgh’=mV²/2 + kx²/2  —  80.10.(16 + x)=80.(-15,1)²/2 + 2.000.x²/2  —  x₁=2,4m  —  x₂=-1,6m (não convém)  —  distância pedida  —  h’=16 + 2,4  —  h’=18,4m

21- 

Como o carro de polícia que emite som de frequência f se aproxima do observador que está parado, este perceberá

um som de frequência maior que a real emitida pelo carro  —  R- B

 

22- Você deve sempre seguir a orientação de regras de sinais indicadas abaixo:

0. Correta  —  v_o negativa (observador se afasta da fonte, suposta parada)  —  v_f negativa  —  a fonte se aproxima do observador, suposto parado)  —  f_o/(u ±v_o) = f_F/(u±v_F)  —  f_o/(u – v_o) = f_F/(u – v_F)  —  f_o/(340 – 30) = 500/(340 – 60)  —

f_o/310 = 500/280  —  f_o=155000/280  —  f_o=553,57Hz.

1. Falsa  —  v_o negativa (observador se afasta da fonte, suposta parada)  —  v_f negativa  —  a fonte se aproxima do observador, suposto parado)  —  f_o/(u ±v_o) = f_F/(u±v_F)  —  f_o/(u – v_o) = f_F/(u – v_F)  —  f_o/(340 – 30) = 500/(340 – 60)  —

f_o/310 = 500/280  —  f_o=155000/280  —  f_o=553,57Hz. (observe que é a mesma situação que a anterior, apenas inverteram-se os sentidos e, é claro que a frequência percebida pelo observador deve ser a mesma).)

23- Esse fenômeno que provoca alterações na frequência das ondas chama-se efeito Doppler  —  equação fundamental da ondulatória  —  v=λ.F  —  1540 = λ.2,2.10⁶  —  λ = 1540/2,2.10⁶=700.10^-6m  —  λ=7.10².10^-6.10³mm  —  λ=0,7mm

R- C.

24- O efeito Doppler refere-se à variação da freqüência notada por um observador quando a distância entre ele e uma fonte de ondas está aumentando ou diminuindo.

Na aproximação entre fonte e observador, o mesmo perceberá o som emitido pela fonte mais agudo (maior freqüência, recebe maior número de frentes de onda na unidade de tempo) do que perceberia se fonte e observador estivessem parados. Nesse caso, o comprimento de onda aparente percebido pelo observador será menor que o comprimento da onda emitido pela fonte (observador O1 da figura abaixo).

No afastamento entre fonte e observador, o mesmo perceberá o som emitido pela fonte mais grave (menor freqüência, recebe menor número de frentes de onda na unidade de tempo) do que perceberia se fonte e observador estivessem parados. Nesse caso, o comprimento de onda aparente percebido pelo observador será maior que o comprimento da onda emitido pela fonte (observador O2 da figura ao lado).

Observe que o motorista da ambulância não percebe nenhuma alteração no som emitido pela sirene, pois eles se movem juntos.

R- B

 

Voltar para os exercícios