Cordas vibrantes – Harmônicos – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Cordas vibrantes – Harmônicos
01- 75 oscilações – 30s — 1 oscilação — T=30/75s — f=1/T — f=75/30 — f=2,5Hz — fn=nf1 — supondo n=1 — f1=2,5Hz — a próxima ocorre quando n=2 — f2=2f1 — f2=2.2,5 — f2=5Hz R- D
02- L=0,6m — som fundamental (1 fuso) — n=1 — fn=nV/2L — f1=V/2L — 220=V/2.0,6 — V=264m/s R- D
03- a) λ/2=12 — λ=24cm=0,24m
b) P=mg — P=0,18.10 — P=1,8N — v = 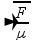 — v =
— v = 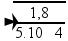 — V=
— V=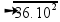 — V=60m/s
— V=60m/s
V= λf — 60=0,24f — f=250Hz
04- Os três maiores comprimentos de onda são os 3 primeiros
1o – λ1/2=90 — λ1=180cm 20 -2λ2/2=90 — λ2=90cm 3o – 3λ3/2=90 — λ3=60cm
05- Som fundamental — n=1 — f1=1/2.0,5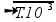 — 200=1/2.0,5
— 200=1/2.0,5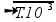 — 4.104=T/10-3 — T=40N=P
— 4.104=T/10-3 — T=40N=P
P=mg — 40=m10 — m=4kg R- B
06-λ1/2=50 — λ1=100cm R- D
07- a) λ = 2.35 = 70 cm
f = 680 Hz
v = λ.f = 0,7.680 = 476 m/s
b) v = λ.f
340 = l680
λ = 340/680 = 0,5 m = 50 cm
08- fn=840Hz — fn+1=1260Hz — fn+1-fn=1260-840=nV/2L — 210=1.210/2L — L=0,5m=50cm
09- Quando tocada na região da boca, comprimento é L e f=440Hz — V=λ1f1 — freqüência fundamental – 1o harmônico –
λ1/2=L — λ1=2L — V=2L.440 — V=880L
Quando tocada na região da boca, quando o comprimento for L/3 a freqüência fundamental será — λx/2=2L/3 — λx=4L/3
V=λx.fx — V=4L/3.fx — 880L=4L/3. fx — fx=660Hz
10- µ=10g/m=0,01kg/m
Adjacentes — uma é n e a seguinte n+1
fn=n/2L. — fn+1=(n+1)/2L.
— fn+1=(n+1)/2L. — fn – fn+1=1/2L.
— fn – fn+1=1/2L. — (125-100)=1/2.2
— (125-100)=1/2.2 (125-100)=1/2.2
(125-100)=1/2.2 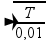 — (100)2=(T/0,01)2 — 104=T/10-2 — T=100N=P — P=mg — 100=m10 — m=10kg R- A
— (100)2=(T/0,01)2 — 104=T/10-2 — T=100N=P — P=mg — 100=m10 — m=10kg R- A
11- a) RESSONÂNCIA
b) I – Todo corpo tem suas freqüências naturais de vibração (modos de vibração).
II – Quando o corpo é submetido a estímulos externos periódicos com freqüência igual a uma de suas freqüências naturais, o corpo oscilará com maior amplitude, quando se diz que o mesmo está em ressonância.
III – No caso, Flavita ajustava a tensão na corda 4 para deixá-la com as mesmas freqüências naturais das da corda 5, pressionada entre o 4o e o 5o traste.
12- A fonte é a mesma (mesma f)—A tração é a mesma (mesmo peso – P/2) — L é o mesmo (distância entre fonte e roldanas iguais)
A corda com três fusos é a mais densa (m1), pois como T é a mesma (v = ) V e m são inversamente proporcionais e V é menor na mais densa. Da equação V=λf, como f é a mesma, menor V implica em menor l, que é o da corda com três fusos (m1).
) V e m são inversamente proporcionais e V é menor na mais densa. Da equação V=λf, como f é a mesma, menor V implica em menor l, que é o da corda com três fusos (m1).
Fio 1 — 3o harmônico — n=3 — fn=nV/2L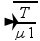 — f3=3V/2L
— f3=3V/2L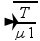
Fio 2 — 1o haemônico — n=1 — f1=1V/2L
f1=f3=f — 1V/2L. = 3V/2L
= 3V/2L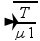 —
—  = 3
= 3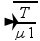 — (
— ( )2 = (3
)2 = (3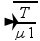 )2 — µ1=µ/9
)2 — µ1=µ/9
13- Sendo V inversamente proporcional a m — VA>VB. Como o comprimento de onda é o mesmo, de V=λf, concluímos que V é diretamente proporcional a f, ou seja, fA > fB. R- C
14- O Sol considerado é a frequência fundamental — λSol/2=0,64 — λSol=1,28m — V=λSolfSol=392.1,28=501,76m/s
Como a corda é a mesma (mesmo meio), a velocidade V é a mesma para a freqüência Lá, também fundamental —
V=λLá.fLá — 501,76=λLá.440 — λLá=1,14m — som fundamental — λLá/2=L — 1,14/2=L — L=0,57m
15- Se o comprimento da corda é igual a meio comprimento de onda, trata-se da freqüência fundamental e λ/2=1 — λ/=2m
V= λ.f — V=2.260 — V=520m/s — V= , — 520=
, — 520=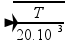 — T=5.408N
— T=5.408N
16- Mesma corda (mesmo meio), a V é a mesma. —- considerando a freqüência fundamental (λ=2L) — λMifMi=λLáfLá — 2L1.660=2L2.880 — L2/L1=3/4
17- a) T=2,5.10-3s — f=1/T — f=1/2,5.10-3 — f=400Hz
b) Nota desafinada – T1 – f=400Hz – µ=5,0.10-3kg/m – som fundamental n=1 — fn=n/2L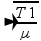 — 400=1/2.1
— 400=1/2.1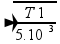 — T1=3.200N
— T1=3.200N
Nota afinada – T2 – f=440Hz – m=5,0.10-3kg/m – som fundamental n=1 — fn=n/2L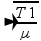 — 440=1/2.1
— 440=1/2.1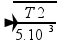 — T2=3.872N
— T2=3.872N
O aumento de tensão na corda será ΔT=T2 – T1=3.872 – 3.200=672N
18- a) som fundamental — λ1/2=50 — λ1=1m — V=λ1f1=1.500 — V=500m/s
b) V=λf — 500=0,5f — f=1000Hz
19- V e L são constantes (mesma corda).
fn+1=(n + 1)V/2L — fn=nV/2L — fn+1/fn = (n+1)V/2LX2L/nV — fn+1/fn+ = (n+1)/n
20- fn=nf1 — fn=n.100 (n=2,3,4,5) R- C
21- Relação entre as equações da frequência e da velocidade — fn=n.V/2L — V=√(T/μ) — fn=1/2L. √(T/μ) — para a corda 1 — f1=1/2L. √(T/μ) — 36=1/2.(0,60).√(40/μ1) — (72.0,60)2=(√40/μ1)2 — μ1=0,021 — frequência fundamental da corda 2 —
f’1=1/2L. √(T2/μ) — f’1=1/2.(0,40).√(90/0,021) — f’1=81 Hz
22- V=√T/μ=√(240/2,4.10-4) — V=√(100.104) — V=10.102 — V=103=1.000m/s — R- A
23- Velocidade de propagação da onda — V=λ.f — V=50.0,5 — V=25m/s — V=∆S/∆t — 25=10/∆t — ∆t=0,4s R- B
24- Observe nas figuras abaixo as ondas estacionárias formadas em cada caso — γ1/2=L — γ1=2L — V1= γ1.f1 — V1=2L.f1
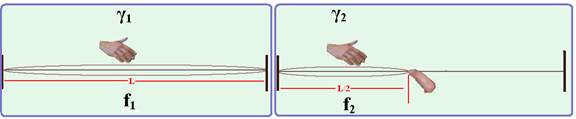
(I) —γ2/2=L/2 — γ2=L — V2= γ2.f2 — V2=L.f2 (II) — como a velocidade de propagação em cada caso é a mesma — V1=V2 — I=II — 2Lf1=Lf2 — 2.220=f2 — f2=440Hz — R- A
25- Observe abaixo a expressão genérica para n harmônicos:
enésimo harmônico — (“n + 1” nós e n fusos)
n.γn/2=L — .γn =2L/n — V=.γn.fn — fn=V/γn — fn=nV/2L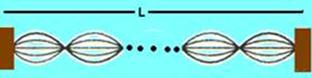
Lembrando que f1=V/2L — fn=nf1
Se você tiver dois harmônicos consecutivos — fn=n.V/2L e f(n + 1)=(n + 1).V/2L — ∆f=(n + 1).V/2L – n.V/2L — ∆f=nV/2L +
V/2L – nV/2L — ∆f=V/2L — 175 – 150=V/2.2 — V=100m/s — R- A
