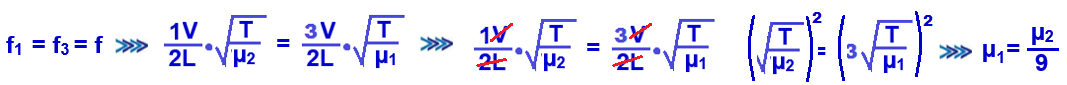Cordas vibrantes
Cordas vibrantes – Harmônicos
No estudo da acústica, uma harmônica de uma onda sonora corresponde à uma frequência específica de vibração que tem a propriedade de causar o fenômeno de ressonância.
Essas frequências são denominadas frequências de ressonância.
Assim, o conjunto de todos os modos de oscilação possíveis é chamado de série harmônica.
Para que você estude detalhadamente os harmônicos deve dividi-los em duas partes, cordas vibrantes e tubos sonoros.
Cordas vibrantes
As cordas vibrantes correspondem à fios flexíveis e tracionados (tensionados) em seus extremos,
utilizados em instrumentos musicais como, violão, guitarra, violino, cavaquinho, banjo, etc.
Harmônicos de uma corda vibrante
Os harmônicos de uma corda vibrante são as várias possíveis freqüências naturais das ondas estacionárias que surgem em cordas tensas (sob ação de forças tensoras de intensidade T), com massa m e comprimento L e densidade linear de massa µ.



Velocidade V de propagação da onda na corda
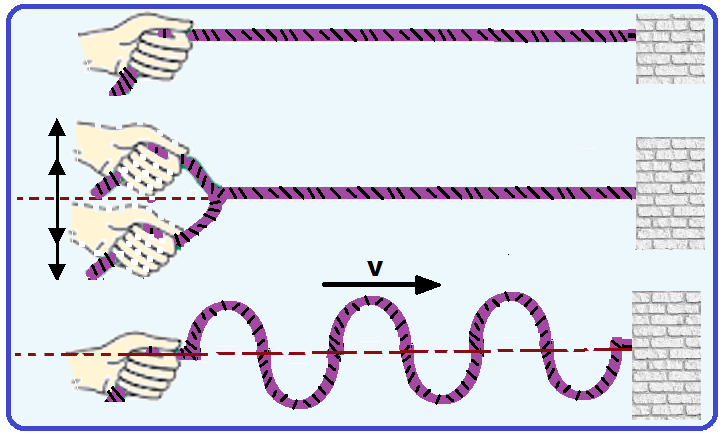
As ondas periódicas são originadas por fontes que executam oscilações periódicas (são repetidas em intervalos de tempos iguais).
Sendo assim, podemos dizer que a propagação de uma onda periódica em um meio homogêneo e isótropo é um movimento uniforme, com a onda se propagando com velocidade constante V, tal que V = ΔS/Δt.
Equação fundamental da ondulatória
Observe na figura as características de uma onda transversal se propagando numa corda, com com velocidade V: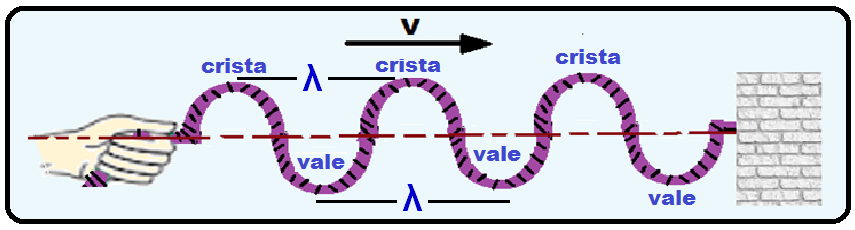
![]() Comprimento de onda (λ)
Comprimento de onda (λ) ![]() distância entre duas cristas ou dois vales consecutivos.
distância entre duas cristas ou dois vales consecutivos.
![]() Período (T)
Período (T) ![]() que é o intervalo de tempo para que cada ponto homogêneo da onda execute uma oscilação completa, ou percorra um comprimento de onda λ.
que é o intervalo de tempo para que cada ponto homogêneo da onda execute uma oscilação completa, ou percorra um comprimento de onda λ.
![]() Frequência (f)
Frequência (f) ![]() número de oscilações completas que cada ponto homogêneo da onda executa na unidade de tempo.
número de oscilações completas que cada ponto homogêneo da onda executa na unidade de tempo.
Observe nas informações acima que, num intervalo de tempo Δt que corresponde a um período T (Δt = T), a onda percorre uma distância ΔS que corresponde a um comprimento de onda λ (ΔS = λ).
V = ΔS/Δt ![]() V = λ/T
V = λ/T ![]() T = 1/f
T = 1/f ![]() V = λ/(1/f)
V = λ/(1/f) ![]() V = λ.f (equação fundamental da ondulatória)
V = λ.f (equação fundamental da ondulatória)

Fórmula de Taylor para cordas vibrantes
Pode-se provar que, para a propagação de um pulso transversal ou de uma onda periódica transversal numa corda, a velocidade (V) com que uma onda periódica se propaga depende da densidade linear de massa (µ) da corda e da intensidade da força tensora (T) a que ela está sujeita.
A relação entre essas grandezas foi provada matematicamente pelo britânico Brook Taylor (1685-1731), onde você pode determinar a velocidade de propagação de uma onda numa corda utilizando a equação conhecida como Fórmula de Taylor, expressa a seguir:

Modos de vibração (harmônicos) em cordas vibrantes
Considere uma corda de comprimento L fixa em seus extremos.
Produzindo-se uma perturbação em qualquer ponto entre os extremos fixos, esta perturbação propaga-se até cada uma das extremidades, refletem-se e retornam em sentido contrário, formando
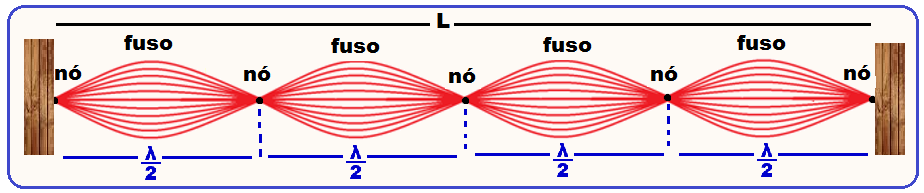
ondas estacionárias com nós (pontos que não vibram) e ventres (distância entre dois nós, que chamamos de fuso, onde todos os pontos estão em movimento vibratório).
As figuras abaixo mostram os diversos modos de vibração numa mesma corda (mesmo meio, mesma velocidade).
A onda estacionária de freqüência mais baixa é chamada freqüência fundamental. Ela corresponde a uma onda estacionaria com um único ventre, o harmônico fundamental ou primeiro harmônico.
As demais freqüências naturais são chamadas sobretons ou harmônicos superiores, pois as freqüências subsequentes são múltiplos inteiros da freqüência fundamental.
![]()

![]()
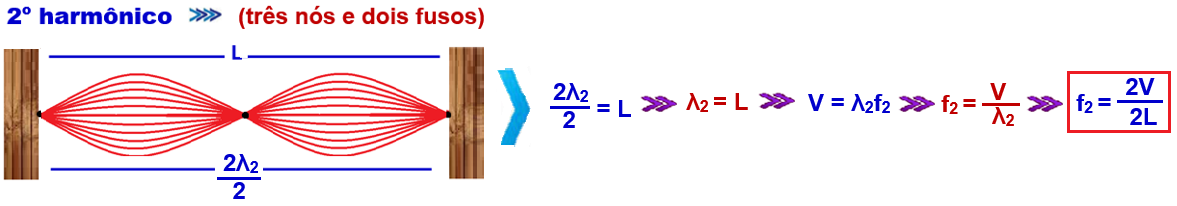
![]()

![]()
Enésimo harmônico ![]() (“n + 1” nós e n fusos)
(“n + 1” nós e n fusos)
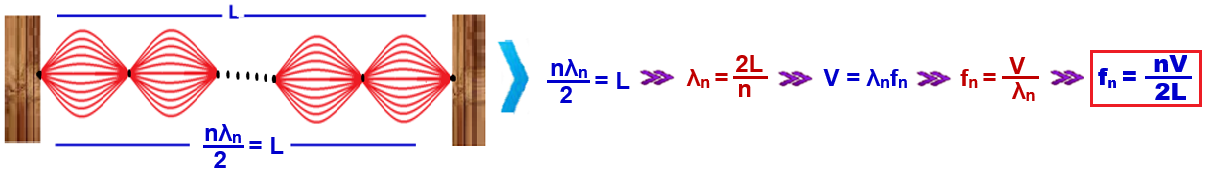
Lembrando que f1 = V/2L ![]() fn = nf1
fn = nf1
Generalizando:

Observe que existe uma relação simples entre o comprimento L da corda e o comprimento de onda λ da onda estacionária de frequência fn que nela se estabelece.
Generalizando, para o enésimo harmônico ![]() n = 1, 2, 3, 4, 5, …
n = 1, 2, 3, 4, 5, …
O número inteiro n corresponde ao número do harmônico: n = 1, para o harmônico fundamental; n = 2, para o segundo harmônico; n = 3, para o terceiro harmônico; e assim por diante.
Da equação de Taylor, para o enésimo harmônico, teremos ![]() V =
V = , que, substituída em fn = n
, que, substituída em fn = n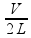 , nos fornece:
, nos fornece:

Observe na expressão acima que temos três variáveis, comprimento da corda L, densidade linear de
massa (corda mais grossa ou mais fina) µ e força de tração T.
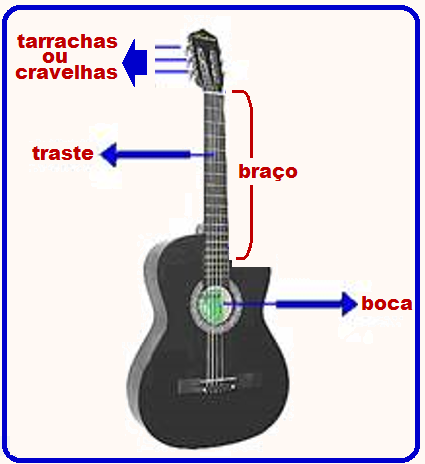
As cordas de um violão, por exemplo, são dedilhadas com o polegar, indicador, médio e anular da mão direita e, para variar o comprimento da corda L, o músico coloca os dedos da mão esquerda fazendo pressão no espaço entre os trastes, produzindo assim as diversas notas musicais.
Para variar a densidade linear µ, o músico muda de uma corda para a outra e, para afinar o instrumento ele varia a força de tração girando as cravelhas ou tarraxas ( roscas para essa finalidade).
Variando dessa maneira essas três grandezas o músico obtém as várias notas musicais (harmônios, freqüências).
O que você deve saber, informações e dicas
 A frequência de uma onda é sempre a mesma frequência da fonte produtora da onda.
A frequência de uma onda é sempre a mesma frequência da fonte produtora da onda.
Dessa forma, independentemente do meio em que a onda se propaga, sua frequência não vai ser modificada.
![]() A velocidade de propagação de uma onda mecânica em um determinado meio só depende das propriedades elásticas do meio.
A velocidade de propagação de uma onda mecânica em um determinado meio só depende das propriedades elásticas do meio.
![]() Procure entender e memorizar as informações e as expressões matemáticas fornecidas acima.
Procure entender e memorizar as informações e as expressões matemáticas fornecidas acima.
 Analise atentamente as resoluções desses exercícios interessantes:
Analise atentamente as resoluções desses exercícios interessantes:
![]() 01- (UNICAMP-SP) Para a afinação de um piano usa-se um diapasão com frequência fundamental igual a 440Hz, que é a frequência da nota Lá.
01- (UNICAMP-SP) Para a afinação de um piano usa-se um diapasão com frequência fundamental igual a 440Hz, que é a frequência da nota Lá.
a) A nota Lá de certo piano está desafinada e o seu harmônico fundamental está representado na curva tracejada do gráfico.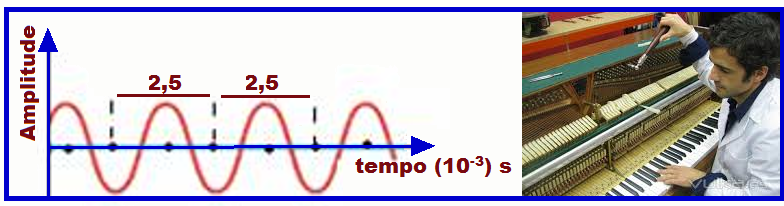
a) Obtenha a freqüência da nota Lá desafinada.
b) O comprimento dessa corda do piano é igual a 1m e sua densidade linear é igual a 5,0.10-2g/cm. Calcule o aumento de tensão na corda necessário para que a nota Lá seja afinada.
Resolução:
a) Observe no gráfico que representa o harmônico fundamental da nota Lá desafinda que o período (tempo decorrido entre duas cristas ou vales consecutivos) vale T = 2,5.10-3s ![]() f = 1/T
f = 1/T ![]() f = 1/2,5.10-3
f = 1/2,5.10-3 ![]() f = 400Hz (frequência do harmônico funfamental da nota Lá desafinada).
f = 400Hz (frequência do harmônico funfamental da nota Lá desafinada).
b) Tração (tensão) T1 da nota Lá desafinada de frequência f=400Hz, densidade linear µ = 5,0.10-3kg/m.
![]()
Tração (tensão) T2 da nota Lá afinada (frequência do diapasão) f = 440H z, densidade linear µ = 5,0.
10-3kg/m.
![]()
O aumento pedido de tensão na corda necessário para que a nota lá seja afinada será ΔT =T2 – T1 = 3.872 – 3.200 = 672N.
![]() 02- (UFMG-MG) Bruna afina a corda mi de seu violino, para que ela vibre com uma freqüência mínima de 680 Hz.
02- (UFMG-MG) Bruna afina a corda mi de seu violino, para que ela vibre com uma freqüência mínima de 680 Hz.
A parte vibrante das cordas do violino de Bruna mede 35 cm de comprimento, como mostrado nesta figura: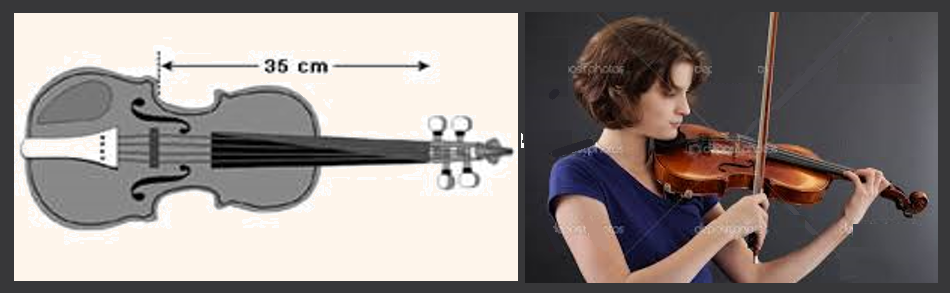
Considerando essas informações,
a) Calcule a velocidade de propagação de uma onda na corda mi desse violino.
b) Considere que a corda mi esteja vibrando com uma freqüência de 680 Hz.
Determine o comprimento de onda, no ar, da onda sonora produzida por essa corda.
Velocidade do som no ar = 340 m/s
Resolução:
a) Pelo enunciado a frequência mínima de vibração que ele fornece é a frequência fundamental f1 = 680 Hz ![]() comprimento da corda L = 35cm
comprimento da corda L = 35cm ![]() comprimento de onda do primeiro harmônico λn = 2L/n
comprimento de onda do primeiro harmônico λn = 2L/n ![]() n= 1
n= 1 ![]() λ1 = 2.35/1
λ1 = 2.35/1 ![]() λ1 = 70 cm
λ1 = 70 cm
V =λ.f ![]() V = 0,7.680
V = 0,7.680 ![]() V = 476 m/s (velocidade da onda na corda mi, constante).
V = 476 m/s (velocidade da onda na corda mi, constante).
b) Dados: frequência de vibração da corda mi f = 680 Hz que é a mesma que no ar, pois a frequência independe do meio de propagação e velocidade de propagação do som no ar V = 340 m/s.
Equação fundamental da ondulatória ![]() v = λ.f
v = λ.f ![]() 340 = λ.680
340 = λ.680 ![]() λ = 340/680 = 0,5 m = 50 cm
λ = 340/680 = 0,5 m = 50 cm
 03-(UFG) Na experiência de ressonância em cordas representada na figura, dois fios de densidades diferentes estão tensionados, através de roldanas ideais, por um bloco que pende deles dois.
03-(UFG) Na experiência de ressonância em cordas representada na figura, dois fios de densidades diferentes estão tensionados, através de roldanas ideais, por um bloco que pende deles dois.
As extremidades esquerdas de ambos estão ligadas a uma fonte que produz pequenas vibrações com freqüência conhecida. 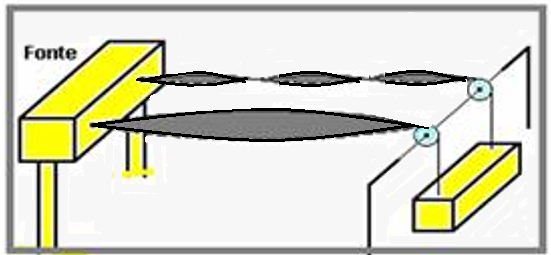
A distância entre a fonte e as roldanas é L. Verifica-se que, quando a freqüência da fonte atinge o valor f, ambos os fios entram em ressonância, o mais denso no terceiro harmônico e o outro, na freqüência fundamental. Dados: v =  (velocidade da onda na corda).
(velocidade da onda na corda).
Conhecendo a densidade linear de massa µ do fio mais denso, determine a densidade linear de massa do outro fio;
Resolução:
Cada fio possui possui a mesma frequência f de oscilação que é a da fonte, f1 = f2 = f ![]() a força de tração também é a mesma para cada fio, pois(suportam o mesmo peso (P/2), T1 = T2 = T.
a força de tração também é a mesma para cada fio, pois(suportam o mesmo peso (P/2), T1 = T2 = T.
O comprimento L de cada fio é o mesmo (distância entre fonte e roldanas iguais).
O fio com três fusos é a mais denso (µ1), pois como T é a mesma (v =  ) V e µ são inversamente proporcionais e V é menor na mais densa.
) V e µ são inversamente proporcionais e V é menor na mais densa.
Da equação V = λf, como f é a mesma, menor V implica em menor λ, que é o da corda com três fusos (µ1).