Teorema de Stevin – Resolução
Resolução comentada das questões de vestibulares sobre
Teorema de Stevin – Pressão Hidrostática – Vasos Comunicantes
01– A pressão hidrostática é fornecida por Ph=dcafé.g.h e observe que ela não depende das dimensões do tubo e da cafeteira e, como os pontos A e B estão abertos, a pressão nos dois é a mesma e ficam na mesma altura — R- A
02– ΔP=Pmáx – Patm=1,02 – 1,00 — ΔP=0,2atm=0,2.105N/m2 — ΔP=dgh — 2.104=103.10.h — h=2m — regra de três — 5m – 0,5atm — 2m – xatm — 5x=2.0,5 — x=1/5=0,2m=20cm — R- C
03- P=d.g.h — 0,05.105N/m2=103kg/m3.10m/s2.h — h=0,5m — h=50cm
04– R- D (veja teoria)
05– A pressão no fundo do recipiente varia linearmente com a altura e independe da área de seção reta de cada cilindro — R- A
06- Como as bases tem a mesma área (S), o líquido é o mesmo (água) e a as alturas das colunas líquidas são as mesmas, a pressão (P) no fundo dos recipientes é a mesma — P=F/S — portanto os valores das forças exercidas pela água nas bases dos recipientes é a mesma (
) — as forças exercidas pelas balanças sobre as bases correspondem ao peso dos volumes dos líquidos contidos em cada recipiente — maior volume, maior peso (
) — R- E
07- Quando você abre a válvula,a água flui da caixa da esquerda para a da direita até que elas tenham a mesma altura — a altura da caixa da esquerda diminui e consequentemente a pressão na base da mesma também diminui — R- A
08– R- E (veja teoria)
09- P=dgh — P=103.10.4 — P=4.104N/m2 — P=F/S — 4.104=F/12 — F=4.104/12.10-4 —– F=48N — R- B
10- a) Com a torneira aberta, o volume de água que preencheu o recipiente II é o mesmo que escoou do recipiente I —
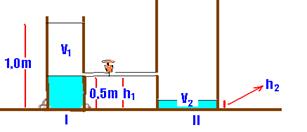
V1=V2 — S1.h1= S2.h2 — πR12.h1= πR22.h2 — R12.0,5= (2R1)2.h2 — h2=0,125m
b) P=Patm + d.g.h — P= 105 + 103.10.1 — P=1,1.105N/m2
11- A cada 10m de profundidade que você desce sob a superfície da água sua pressão devido à coluna líquida aumenta de 1 atm — PValdirene= 1.000atm – Patm(1atm) — PValdirene=999atm — regra de três — 1atm – 10m — 999atm – x —
x=999 x 10 — x=h=9.990m
12– a) P= Patm + dgh — 4.105 = 105 + 103.10.h — h=3.105/104 — h=30m
b) Para sofrer na subida vertical uma variação de pressão ΔP=104N/m2, em Δt=1s, ele deve se deslocar — ΔP=d.g.h — 104=103.10.h — h=1m — V= Δh/Δt — V=1/1 — V=1m/s
13- Pressão exercida pelo êmbolo na profundidade h — P=Patm + F/S — P=Patm + 6,28/π.(R)2=Patm + 6,28/3,14.2/2.10-4 — P= Patm +2.104 — Pressão exercida pelo líquido na profundidade h — Plíq=Patm + dgh=Patm + 1,25.103.10.h — Plíq=Patm + 1,25.104.h — P=Plíq — Patm + 2.104=Patm + 1,25.104.h — h=2/1,25 — h=1,6m
14- Psanguínea=Phidrostática — ds.g.hs=dHg.g.hHg — 103.0,5=13,6.103.hHg — hHg=0,0367mHg — hHg=36,7mmHg
15– P=d.g.h — 9.103=103.10.h — h=0,9m — R- E
16- A pressão do ar aprisionado no barco à profundidade h=(2,20 – 1,70)=0,5m é dada por P= Patm + d.g.h — P -Patm=d.g.h=103.10.0,5 — P – Patm=5,0.103N/m2
17- P=1atm=105N/m2 — h=10m — P=dgh — 105=d.10.10 — d=1,0.103k/m3 — d’=0,8d — P’=105N/m2 — P’=d’.g.h’ — 105=0,8.103.10.h’ — h’=105/8.103 — h’=12,5m — R- D
18- P=Patm + dgh=1,01.105 + 1,00.103.10.(1,0 + 2,0) — P=1,01.105 + 3,00.104 — P=1,01.105 + 0,30.105 — P=1,31.105N/m2 — R- D
19- P1=ρ.g.h — P2=1,2ρ.g.h’ — P1/P2=ρ.g.h/1,2ρ.g.h’ — P1=P2=P — 1= ρ.g.h/1,2ρ.g.h’ — h’=1/1,2h10/12h=5/6h — h – 5/6h=(6h – 5h)/6=h/6 — h’=h/6 — R- B
20- R- A (veja teoria)
21- Do gráfico — Patm=0,5.105=5,0.104N/m2 — quando h=15m – P=5,0.105N/m2 — P=d.g.h — 5.105=d.10.15 — d=0,033.105=3,3.103kg/m3
22- Como haverá redução na altura do nível de líquido na caixa da esquerda, pela lei de Stevin, p =
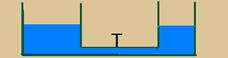
d.g.h, haverá menor pressão no fundo da caixa — R- A
23- Aumentando-se a altitude, diminui a espessura da camada atmosférica sobre a superfície, diminuindo a pressão — Curitiba encontra-se na altitude de 945m — R- C
24- Dados — A = 2,4 m2 — h = 1,8 m — d = 1,2 g/cm3 = 1.200 kg/m3 — g = 10 m/s2 — a força máxima suportada correspode ao peso do líquido — F = P = m.g = d.V.g = d.A.h.g = 1.200.(2,4).(1,8).(10) — F = 51.840 N — 50.100 N < F < 52.000 N — R- D
25- Dados — Z = 100 mL/s = 0,1 L/s — d = 1 kg/L = 103 kg/m3 — Pcol.deágua = 103Pa — g = 10 m/s2 — pelo teorema de Stevin a pressão da coluna líquida é — Pcol.deágua=dgh — 103=103.10.h — h=0,1m — caixa cúbica de volume 1m3 tem área da base Ab=1m2 — cálculo do volume derramado — V=Ab.h=1.(0,1) — V=0,1m3=100L — a vazão (Z) é a razão entre o volume derramado e o tempo — Z=V/Δt=100/0,1 — Δt=103s — R- D
26- De acordo com Teorema de Stevin, pontos de mesmo líquido em repouso que estão na mesma horizontal estão sob mesma pressão — então, no ponto A da horizontal que passa pela interface entre a água e o líquido mais denso, a pressão deve ser a
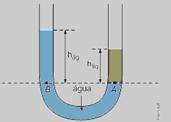
mesma que no ponto B situado na água, na mesma horizontal — pA = pB — 
— como dliq > dág —
hlíq < hág — R- D
27- Dados — dag = 1 g/cm3 = 103 kg/m3; — dglic = 1,3 g/cm3 = 1,3.103 kg/m3 — hág= 10 cm = 10-1 m; hglic = 1 m — g = 10 m/s2 — patm = 1,01.105 Pa — pressão da coluna de água — Pág=dágghág=(103).10.(10-1) — Pág=1,0.103Pa=0,01.105Pa — pressão da coluna de glicerina — Pglic=dglicghglic=(1,3.103).(10).(1) — Pglic=1,3.104Pa=0,13.105Pa — na superfície que separa água-glicerina a pressão a pressão é P1=Patm + Pág=1,01.105 + 0,01.105 — P1=1,02.105Pa — no fundo do recipiente, a pressão (p2) é vale — P2=Patm + Págua + Pglic — P2=1,01.105 + 0,01.105 + 0,13.105 — P2=1,15.105 Pa. — R- E
Obs: segundo o Sistema Internacional de Unidades o plural das unidades é feito apenas acrescentando a letra s no final, quando não terminada em s. Caso seja terminada em s, não sofre flexão, e quando grafadas por extenso, deve ser em letras minúsculas. Exemplos: pascal – pascals; decibel – decibels; newton – newtons.
28- Dados: m = 900 kg; A1 = 2.500 cm2 = 25.10-2 m2 ; A2= 25 cm2 = 25.10-4 m2; dóleo = 900 kg/m3; h = 4m — de acordo com o teorema de Stevin, pontos de um mesmo líquido em repouso que estão na mesma horizontal suportam a mesma pressão — a
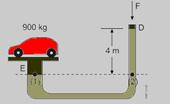
pressão no ponto (1) provocada pelo peso do carro é igual à pressão no ponto (2) provocada pela força 
, somada à da coluna líquida — P1=P2 — mg/A1=F/A2 + dóleogh — 9000/25.10-2=F/25.10-4 + 900.10.4 — 36.000 – 36.000=F/25.10-4 — F=0 —
R- A
29- 76cm Hg ————– 10m de H2O—————–1,0atm—————– 105N/m2
X Hg——————- 5 m de H2O ————–Yatm——————–Z N/m2
X=76×5/10 — X=38cmHg — Y=5×1/10 — Y=0,5atm — Z=0,5×105/1 — Z=0,5.105N/m2 — apressão no fundo é a soma da pressão atmosférica com a pressão da coluna de água — P=1,0 + 0,5 — 1,5atm — P=76 + 38 — P=114cmHg —
P=105 + 0,5.105 — P=1,5.105Nm2 — R- B
30- A diferença de pressão hidrostática (ΔP) entre dois pontos de desnível h, para um líquido de densidade dliq, é dada pelo teorema de Stevin — ΔP = dliq.g.h — assim,, essa diferença só depende da densidade do líquido, do desnível e da gravidade local — R- B
31- h = 2.000 m — g = 10 m/s2; r = 0,9 g/cm3 = 9 ´102 kg/m3 — teorema de Stevin — DP = r g h = 9 ´102 ´ 10 ´ 2 ´ 103 = 180 ´ 105 — DP = 1,8 ´ 107 Pa — R- B
32- Ptorneira = Págua + Patm — F/S = dgh + Patm — 80/4.10-4 = 1.103.10.h + 1.105 — 2.105=104h + 1.105 — h=105/104 — h=10m
R- E
33- Observe na figura abaixo que a pressão no ponto B no interior do líquido é fornecida por PB =
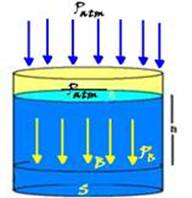
Patm + dlíquido.g.h — essa expressão é chamada de Teorema Fundamental da Hidrostática ou de Teorema de Stevin — uma das conseqüências do teorema de Stevin é de que todos os pontos de uma superfície horizontal (a uma mesma altura h) suportam a mesma pressão, desde que o líquido seja o mesmo.
R- D
34- Teorema de Stevin — observe a figura abaixo:
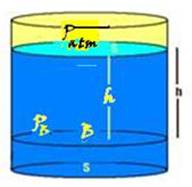
Teorema de Stevin — A pressão no ponto B devida apenas à coluna líquida Plíquido=dlíquido.g.h é chamada depressão hidrostática e PB=Patm + dlíquido.g.h é chamada de pressão total, pressão absoluta ou simplesmente pressão.
A pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h).
O gráfico da pressão total P em função da altura “profundidade” h, (P=Patm+ d.g.h, que é uma função do primeiro
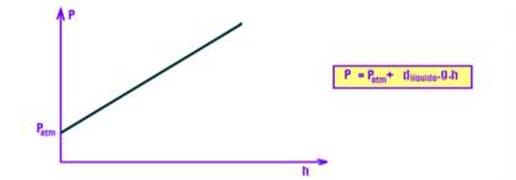
grau)), é uma reta inclinada.
A pressão devido á coluna líquida é maior quanto maior for a profundidade, ou seja, a maior a altura da coluna líquida,
Observe na teoria acima, que a pressão que a água deve exercer para acionar o sifão depende apenas da altura da coluna líquida, não dependendo das dimensões do recipiente, ou seja, do volume de água nele armazenada — assim, mesmo
um pequeno volume de água armazenado, mas com altura suficiente pode acionar o sifão — portanto, a economia deve-se ao volume de água armazenada no tanque — R- B.35-(EsPCEx-012)
Teorema de Stevin — P = Po + d.g.h — 2,2.105 = 1,0.105 + d.10.5 — d=1,2.105/50 — d=0,024.105=2,4.103kg/m3
R- E.
36- A) Pressão sobre o mergulhador que se encontra a uma profundidade de 30 m é determinada a partir da expressão — P = Po + μgh – (Teorema Fundamental da Hidrostática ou de Teorema de Stevin), onde Po é a pressão atmosférica ao nível do mar, μ é a
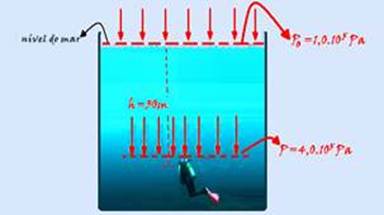
densidade da água do mar 1,0.103kg/m3, h é a profundidade em que se encontra o mergulhador e g é a aceleração da gravidade 10 m/s2 — P=1.105+103x10x30 — P=1.105+3.105 — P=4.105 N/m2 ou P=4 atm — a pressão hidrostática (devida somente à coluna de água) é P=3,0.105N/m2 (Pa) ou P=3,0 atm e a pressão (absoluta, total) é P=4,0.105N/m2 (Pa)ou P=4,0 atm. — Observação: à cada 10m de profundidade na água, a pressão devido à coluna líquida aumenta de 105Pa ou de 1 atm — Exemplo: Se um peixe está a 20m de profundidade da superfície líquida da água, ele suporta uma pressão
hidrostática de Ph=2,0.105Pa ou 2atm. A pressão total deve ser acrescida da pressão atmosférica na superfície — Pt=105Pa + 2.105Pa=3.105Pa ou de 3 atm.
B) Trata-se de uma transformação isotérmica (temperatura constante) — Po.Vo/To = P.V/T — T= To — Po.Vo = P.V=constante (Lei de Boyle) — pressão na superfície — Po=1 atm — volume na superfície — Vo — à uma profundidade onde a pressão é P, o volume é V=25% de Vo=0,25Vo — Po.Vo = P.V — 1.Vo=0,25Vo.P — P=4 atm — observe que essa pressão é exatamente igual à pressão sobre o mergulhador a 30m de profundidade, então ele não poderá ultrapassar essa profundidade sem que o seu pulmão possa vir a sofrer danos