Teorema de Arquimedes – Empuxo – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Teorema de Arquimedes – Empuxo

01- R- C – Veja teoria

02– R- C – (Veja teoria)

03- (O1)- Correta – em seu interior existe ar, que faz diminuir sua densidade média, ficando menor do que a da água.

(02)- Correta – ele está flutuando e em equilíbrio, então a força resultante sobre ele é nula.

(04)- Correta – o empuxo é igual ao peso do volume de líquido deslocado e, no caso é igual ao próprio peso, pois ele está em equilíbrio.

(08)- Falsa – Veja (04)

(16)- Correta – nesse caso, sua densidade média será a da água mais a das chapas de aço

(32)- Falsa – ele desloca apenas a parte de água e o volume do navio é diferente do volume de água deslocada e, se o volume é diferente as densidades devem ser diferentes para manter a igualdade – d_navio.V_navio.g=d_água.V_{água deslocada}.g

(01+02+04+16)=23

04- Enquanto ele está no ar a tensão no cabo é constante e tem valor máximo  —  à medida que o bloco vai penetrando na água, ele vai deslocando mais líquido, o empuxo vai aumentando e a tensão no cabo diminuindo  —  quando ele está totalmente imerso e descendo, o empuxo é máximo (independente da profundidade) e a tensão é constante e mínima.

R- C

05- Sendo o líquido que envolve o recipiente a água e o líquido que o está preenchendo também a água (mesma densidade), para cada unidade preenchida com água, o recipiente desce também uma unidade  — Observe atentamente a sequência de figuras abaixo e verifique que a resposta é a C 

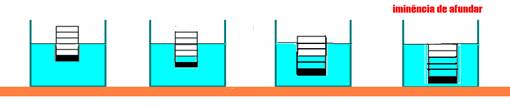
R- C

06- A diferença na leitura da balança corresponde a ao empuxo sofrido pela mão ao ser mergulhada, (veja teoria)     

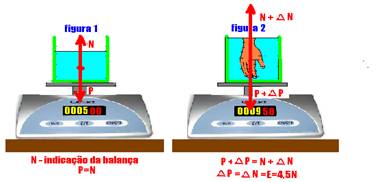
  —  Volume de líquido deslocado=volume da mão =V  —  E=d­_água.V.g  —  4,5=10³.V.10  —  V=4,5.10^-4m³  —  V=4,5.10^-4.10⁶  —  V=4,5.10²cm³ ou V=450 cm³  

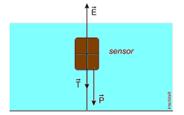
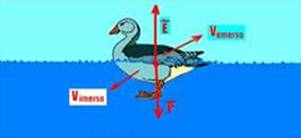
07- A maioria dos peixes ósseos apresenta bexiga natatória (atualmente denominada vesícula gasosa), uma bolsa cheia de gases acima do estômago cujo volume é regulado por meio de trocas de gases com o sangue e, pela sua dilação ou contração, determina a posição do peixe na água. Para aumentar a profundidade, os peixes contraem a bexiga natatória e, com isso, aumentam a sua densidade tornando-se mais pesado que a água e descendo. Ao subir, fazem o contrário.

R- A

08- R- E – Veja teoria

09- R- B – Veja teoria

10- Estando o contrapeso em equilíbrio, em cada líquido, o peso é igual ao empuxo  —  como o contrapeso é o mesmo, o peso é o mesmo e, portato o empuxo é o mesmo  —  R- D

11- Sua densidade é menor que a de B, então ele flutua em B, e maior que a de A, então ele afunda em A  —  R- E

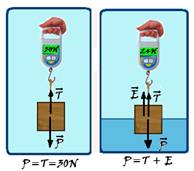
12- Na figura I, N_o é a indicação da balança  —  N_o=P

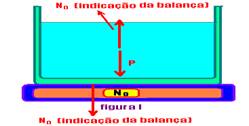
Na figura II, se o corpo imerso recebe do líquido uma força vertical e para cima (Empuxo), pelo princípio da ação e reação o corpo reage sobre o líquido com força de mesma intensidade(Empuxo), mesma direção (vertical) e sentido sentido contrário (para baixo).

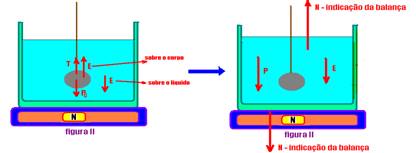
A balança indica apenas as forças que agem no líquido, indicadas na figura da direita acima, que são: peso P do sistema (recipiente mais líquido), empuxo sobre o líquido (E) e a reação normal da balança (indicação da balança N)  —  N=P + E  —  da figura I  —  N_o=P  —  N=N_o + E  — N – N_o=E  —  assim, o empuxo é fornecido pela diferença entre as indicações da balança antes e depois de imergir a esfera.

R- (4 + 8)=12

13- O peso do bloco é constante  —  à medida que o cilindro vai imergindo na água, o empuxo vai

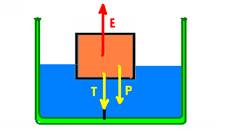
aumentando e consequentemente a tração no fio também vai aumentando, mas a diferença entre eles, que é o peso permanece constante  —  T + P=E  —  T – E=P (constante)  —  R- C

14-  01- Falsa – era graças ao empuxo que ele recebia do ar, vertical e para cima, maior que seu peso.
02- Falsa – o princípio de Arquimedes é válido para qualquer corpo imerso em qualquer fluido (líquidos e gases).

04- Correta – ele é causado pela variação da pressão com a profundidade ou altitude, sendo que nos pontos inferiores do corpo, a força que causa o empuxo é maior que nos pontos superiores.

08- Falsa – o empuxo é igual ao peso do volume de ar deslocado.

16- Correta – E=d.V.g=1,3×2.000×10  —  E=2,6.10⁵N.

32- Falsa – Veja 01.

64- Correta – diminuindo parte do gás, diminuía o volume dos balões, diminuindo assim o volume de ar deslocado, o que implica em diminuir o empuxo.

15- 01- Correta – P=mg=4.10  —  P=40N

02- d=m/V=4/5=0,8kg/m³  —  Falsa

04- E=dVg=1,3.5.10  —  E=65,0N  —  Correta

08- Falsa – para mantê-lo em equilíbrio, o empuxo é igual ao peso.

16- Verdadeira – não haveria fluido para ser deslocado.

(01 + 04 + 16)=21

16- Se as caixas tem a mesma massa, têm o mesmo peso (P=mg) e, se estão em equilíbrio, o peso de cada uma é igual ao respectivo empuxo  —  R- C

17- a) Sim ,ele flutua quando nas câmaras a água é expulsa e substituída por ar, tornando o peso do submarino menor que o empuxo.

b) Não depende, pois o volume de líquido deslocado (empuxo) é o mesmo em qualquer profundidade.

c) Ponto C, devido ao teorema de Stevin  —  P=d.g.h  —  d e g são os mesmos  —  maior h, maior pressão  

18- Forças que agem sobre o bloco  —  peso P (vertical e para baixo)  —  N força que o bloco troca

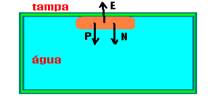
com a tampa (vertical e para baixo)  —  empuxo E (vertical e para cima)  —  P + N=E  —   mg + N=d.V.g  —  d_bloco.V._.g + N=d_água.V.g  — 

N=d_água.V.g – d_bloco.V.g  —  N=(1,0.10³ – 0,25.10³).V.g  —  N=0,75.10³.V.g  —  P= 0,25.10³.V._.g  —  N/P=(0,75.10³.V.g)/(0,25.10³.V.g)  —  N/P=3

19- O empuxo, com o submarino totalmente submerso, é sempre o mesmo (peso do volume de líquido deslocado), expulsando a água, o peso torna-se menor que o empuxo.  —  R- E

20- a) As forças que atuam sobre o submarino são o peso e o empuxo e, como ele se encontra em repouso (equilíbrio estático), os módulos destas forças são iguais. Portanto E = P.
b) O empuxo diminui pois o volume de líquido deslocado é menor.
21- Ambos aumentaram o empuxo sobre a massa. Arquimedes aumentou a densidade do líquido e Ulisses aumentou o volume de líquido deslocado.

22- Com água  —  P_tubo=E  —  d_tubo.V_tubo.g=d_água.V_imerso.g  —  d_tubo.S.h.=1.S.10  —  d_tubo=10/h  —  com líquido  —  d_tubo.V_tubo.g=d_líquido.V_imerso.g  —  d_tubo.S.h.g=d_líquido.V_imerso.g  —  d_tubo.S.h=d_líquido.S.8  —  (10/h).S.h=d_líquido.S.8  —  d_líquido=1,25g/cm³  —  R- E

23- Colocando as forças que agem sobre o cubo  —  peso (P) vertical e para baixo  —  indicação do dinamômetro (força de

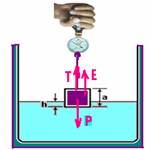
tração no fio) – T=18N  —  empuxo (E) vertical e para cima  —  equilíbrio  —  T + E=P  —  18 + d_água.V_imerso.g = m_c.g  —  18 + 10³.S.h_imerso.10=m_c.10  —  18 + 10³.(0,1).(0,1).0,02 = 10.m_c  —  m_c=2010  — m_c=2kg  —  R- A

24- Começando pela letra b:

b) bloco flutuando com 3/4 de seu volume submerso  —  equilíbrio  —  P=E  —  d_b.V_b.g=d_a.V_imerso.g  —

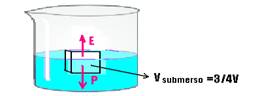
d_b.60.10^-6=10³.(60.10^-6/4)  —  d_b=180.10³/240  —  d_b=0,75.10³kg/m³ ou d_b=7,5.10²kg/m³ ou d_b=0,75g/cm³

a) corpo totalmente suberso e atado pelo fio ao fundo do recipiente  —  T = E – P —  T = d_a.V.g – d_b.V.g  —

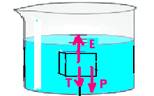
 T=10³.60.10^-6.10 – 0,7510³.60.10^-6.10  —  T= 0,6 – 0,45  —  T=0,15N ou T=1,5.10^-1N

25- O módulo do empuxo sobre o corpo imerso é igual ao módulo do peso do fluido deslocado. Tanto a esfera quanto o barquinho deslocaram a mesma quantidade de água, pois os níveis de água nos dois recipientes subiram a mesma altura.

Desse modo, os módulos dos dois empuxos são iguais ao módulo do peso dessa mesma quantidade de água, ou seja, E_e = E_b .

26- a) volume de água deslocada  —  V_imerso=S.H=8.10^-3.5.10^-2  —  V_imerso=4.10^-4m³  —  estando o recipiente em equilíbrio  —  P=E  —  mg=d_água.V_imerso.g  —  m=1.000.4.10^-4  — m=0,4kg

b) nesse caso, o recipiente está na iminência de afundar, e sua massa será m_c (massa dos

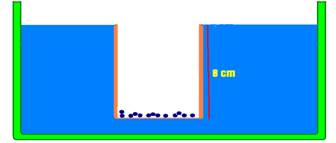
 chumbinhos) + m (massa do recipiente)  —  V_imerso= S.h=8.10^-3.8.10^-2  —  V_imerso=64.10^-5m³  —  peso do recipiente + peso dos chumbinhos=P_s=(m + m_c).g  —  equilíbrio  —  P_s=E  —  (m + m_c).g=d_água.V_imerso.g  —  (0,4 + m_c)=1.000.64.10^-5  —  m_c=0,64 – 0,4  — 

m_c=0,24kg=240g  —  n_chumbinhos=240/12  —  n_chumbinhos=20

c) não mudariam  —  observe na expressão seguinte que a aceleração da gravidade se cancela  —  P=E  —  d_cV_c.g_marte=d_água.V_água.g_marte  —  assim , g não interfere na rwesolução.

27- Colocando as forëas que agem sobre o cilindro —  peso (P) vertical e para baixo  —  empuxo (E)

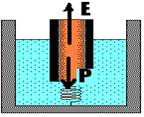
 vertical e para cima —  como a mola não está deformada ela não influi na resolução  —  P=E  —   d_cVg=d_a.V.g  —  0,5.1.16.g=0,8.1.h.g  — 8= 0,8h  —  h=10cm

28- Rompendo o fio as foças que agem sobre a bolinha durante sua subida no trecho (2) são  —  peso (P) e empuxo (E)  —  F_R=ma  —  E – P=ma  —  d₂Vg – mg=ma  —  d₂=5d₁  —  d₁=m/V  —  d₁=0,01/V  —  V=0.01/d₁  —  5d₁.0,01/d₁.10 – 0,01.10=0,01.a  —  0,5 – 0,4=0,01.a  —  a=40m/s²  —  aplicando Torricelli ainda no meio (2)  —  V²=V_o² + 2.a (h – 0,2)  —  8²=0² +2.40.(h – 0,2)  —  h=0,8 + 0,2  —  h=1,0m

29- Estando o iceberg flutuando, ele está em equilíbrio  —  P=E  —  m_gelo.g=d_água.V_imerso.g  —  d_gelo.V_gelo=d_água.V_imerso  —  d_gelo/d_água=V_imerso/V_gelo  — 0,92/1,03= V_imerso/V_gelo   —  0,893=fração submersa/fração total=89,3%

30- a) A massa do recipiente, da água e do barquinho sobre a balança é a mesma, quer o barquinho esteja flutuando, quer esteja submerso. Portanto, M₁ = M₂ .

b) Quando o barquinho está flutuando, o empuxo sobre ele é igual a seu peso e, portanto, maior do que o empuxo quando submerso. Sendo maior o empuxo no barquinho flutuando, o volume da água por ele deslocado nesse caso é maior do que o volume da água por ele deslocado quando está submerso. Uma vez que o volume dentro do recipiente sob o nível da superfície livre da água é o volume da água acrescido do volume de água deslocado, concluímos que o volume dentro do recipiente sob o nível da superfície livre é maior com o barquinho flutuando do que com o barquinho submerso. Assim,a altura da superfície livre com o barquinho flutuando é maior do que a  altura da superfície livre com o barquinho submerso, ou seja, h₁ > h₂ .

31- O acréscimo de peso na balança corresponde ao empuxo, que é igual ao peso do volume de líquido deslocado e, observe, que ele é maior em 2 do que em 3  —  R- B

32- Sem carga  —  P=E=d_a.V_i.g=10³.S.d_o.10=10³(20.5).d_o.10  —  P=10⁶.d_o  —  com carga de 10 automóveis  —

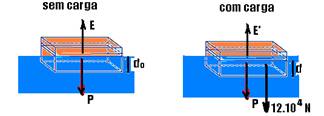
P’=10×1.200×10=12.10⁴N  —  E’=P + 12.10⁴  —  d_a.S.d=P + 12.10⁴  —  10³.(20.5).d=10⁶.d_o + 12.10⁴  —  10⁶d – 10⁶d_o=12.10⁴  —  10⁶(d – d_o)=12.10⁴  —  (d – d_o)=12.10⁴/10⁶  —  (d – d_o)=12.10^-2m=12cm  —  R- C

33- a)

b) A redução da indicação do dinamômetro representa o empuxo E=0,075N=75.10^-3N  —  E=d.V.g  —  75.10^-3=

=d.10^-5.10  —  d=75.10^-3/10^-4  —  d=7,5.10²kg/m³

34- Cálculo do empuxo que age sobre cada bexiga  —  E=d.V.g=1,2.2.10^-3.10  —  E=2,4.10^-2N  —  peso da menina  —  P=mg=24.10  —  P=240N  —  número de bexigas  —  n=240/2,4.10^-2  —  n=240/0,024  —  n=10.000 bexigas

35- Em ambos os casos o peso do sistema é equilibrado pelo empuxo aplicado pela água.

P = E = d_ll V g  em ambos os casos o volume imerso é o mesmo e a altura h não se altera.

V (1º caso) = V (2º caso)  —  3/5.5V=x  —  x=3V  —   como o bloco menor tem volume V, então, um volume  2V do bloco maior ficará imerso, o que corresponde a uma fração y do volume total (5V) dada por  —  y=2V/5V  —  y=2/5  —  R- A

36- Colocando as forças que agem sobre o cilindro  —  E₁ + E₂=P  —  ρ₁V₁.g + ρ₂.V₂.g = ρ(V₁ + V₂).g  —  ρ₁.S.h/3 + ρ₂.S.2h/3= ρ.S.h  —  ρ₁/3 + ρ₂.(2/3)= ρ  —  ρ= (ρ₁ + 2ρ₂)/3  —  R- D

37- Como a vela se mantém sempre em equilíbrio à medida que vai queimando  —  E=P  —  d_água.V_i.g = d_chumbo.V_chumbo.g + d_vela.V_i.g  —  d_água.S.(e + y).g=d_chumbo.S.e.g + d_vela.S.(x + y).g  —  d_águae + d_águay=d_chumboe + d_velax + d_velay  — (d_chumbo –d_água)e + d_velax = (d_água – d_vela )y  —  observe nessa expressão que, se x diminui, y também diminui ( à medida que a vela queima,em relação à superfície da água, a altura da chama (x) diminui e a parte imersa (Y) também diminui e sobe)  —  quando quando a chama chega à superfície da água (x=0), ainda existe parte imersa, pois, y≠0  —  R- D

38- Se o peso do conjunto (boia + flutuador) é desprezível, sobre ele, com volume imerso V_i=10^-3m³,

age apenas o empuxo (E), vertical e para cima  —  sobre a alavanca, no ponto C, reage a força da válvula (F), horizontal e para a esquerda  —

E=d.V.g=10³.10^-3.10  —  E=10N  —  d_BC=1  —  d_AB=5  —  a soma dos momentos das forças E e F em relação ao polo B deve ser nula  —  M_E + M_F=0  —  E.d_AB=F.d_BC  —  10.5=F.1  —  F=50N  —  R- A

39- Forças que agem sobre o submarino:

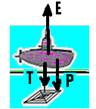
(01)- d_a=3d_s  —  cálculoda força de tração no fio  —  equilíbrio  —  E= P + T  —  d_a.Vg= d_sVg + T  —   3d_sVg –  d_sVg = T  —  T=2d_sVg (tração à que o fio está submetido)  —  o fio suporta  —  T=3P  —  T=3d_sVg  —  a tração que ele suporta é maior que a traação à que ele está submetido  —  o fio não não rompe  —  Falsa

(02)- Verdadeira- Veja (01)

(04)- E=3d_sVg  —  P=d_sVg  —  o módulo do empuxo é 3 vezes maior que o módulo da força peso  —  Falsa

(08)- Verdadeira – veja (01)

(16) Falsa – massas diferentes, pois as densidades são diferentes

(32) Falsa – empuxo é igual ao peso do volume de água deslocada e P=mg

(02) + (08) = 20

40- a) P=P_atm + d.g.h=1.0.10⁵ + 10³.10.2  —  P=1,0.10⁵ + 0,2.10⁵  —  P=1,2.10⁵Nm²

b)Forças que agem sobre o homem:

P_a=T=40N  —  T + E=P  —  40 + d_aVg=mg  —  40 + 10³.V.10=80.10  —  10⁴V=800 – 40  —  V=760.10^-4m³=76L

41- Como as bolas possuem densidades diferentes, sofrem empuxos diferentes e a mais densa fica em baixo e a menos densa em cima, do álcool líquido  —  R- D

 

42- Densidade da criança  —  d_c=m/V  —  quando inspira a criança aumenta seu volume diminuindo sua densidade  —  sendo o peso do ar inspirado praticamente desprezível, o peso da criança não se altera  —  E=P  —  d_água.V_imerso.g=d_corpo.V_corpo.g  —  V_imerso/V_corpo=d_corpo­/dagua  —  observe nessa expressão que, se a densidade do corpo diminui, a razão entre o volume imerso (V_imerso) e o volume total (V_corpo) também diminui  —  R- C

 

43- Observe na figura a forças que agem sobre a esfera totalmente imersa  —  d_e = 5 g/cm³e d_a = 1

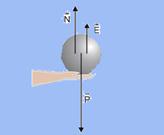
g/cm³  —  como a esfera está em equilíbrio  —  N + E = P  —  N = P – E  —  N = d_e V g – d_a V g  —  N = (d_e – d_a)V g  —  N/P=(d_e – d­_a)Vg/d_eVg  — 

N/P=(5 – 1)/5  —  N/P=0,8  —  R- C

44- A figura mostra as forças agindo nos objetos A e B  —  P_A e P_B  —   módulos dos pesos de A e B,

P_ág  —  módulo do peso da água em cada recipiente  —  E_A e E_B: módulos dos empuxos aplicados pela água nos objetos A e B, respectivamente  —  N_A e N_B: módulos das reações aos empuxos em A e B, respectivamente  —  T_A e T_B: módulos das forças que as hastes exercem em A e B, respectivamente  —  V_A e V_B são os volumes de A e B, respectivamente  —  como esses volumes são iguais  —  V_A = V_B = V  —  d_ág­, d_A e d_B  são as densidades da água, e dos objetos A e B, respectivamente  —  m_ág é a massa de água contida em cada recipiente, ambas iguais  —  g é a aceleração da gravidade local  —  analisando cada uma das afirmativas:

(01) Errada  —  a indicação da “balança” é a intensidade resultante da força normal aplicada no prato  —  cada um dos pratos recebe uma normal devida ao peso da água e outra normal devida ao empuxo  —  lembre-se que: {E = d_liq V_imerso g} e {P = d_corpo V_corpo g}  —  como os corpos estão totalmente imersos, V_imerso = V_corpo  —  indicação da “balança” da esquerda  —   

Sendo V_A=V_B, as duas balanças fornecem a mesma indicação.

(02) Correta  —  como os objetos estão em equilíbrio, as forças atuantes em cada um deles estão equilibradas. Note que o objeto A, de cortiça, tem densidade menor que a da água. Por isso a tendência dele é flutuar. Logo a haste exerce nele força de compressão para baixo . Já, o objeto B, de chumbo, mais denso que a água, tende a afundar. Assim, a haste exerce nele força de tração para cima   —  o chumbo tem densidade bem superior à da água, certamente mais que o dobro. Assim, a diferença entre as densidades do chumbo e da água é maior que 1  —  (d_B – d_ág­) > 1  —  T_A < T_B.
(04) Errada  —  como já destacado em (01), os volumes deslocados de água são iguais, portanto a água exerce forças de mesma intensidade nos dois objetos.

(08) Errada  —  antes, a indicação de cada “balança” era apenas a de massa de água, a mesma nas duas “balanças”. Fazendo-se a imersão dos corpos, como os empuxos são iguais, os acréscimos nas duas balanças também serão iguais.

(16) Correta. E empuxo é igual ao peso de líquido deslocado. Assim, o acréscimo de massa corresponde a massa de água deslocada. 

R- (02 + 16) = 18

45- (01) Errada  —  o líquido menos denso fica em cima e sua superfície livre fica num nível mais alto  —  assim: d_B < d_A.

(02) Correta  —  note na figura que o desnível entre os pontos 1 e 3 (h_1,3) é igual ao desnível entre os pontos 2 e 4 (h_2,4)  —  h_1,3 = h_2,4 = h  —  pelo teorema de Stevin, as pressões nos pontos 3 e 4 são iguais  —  p₃ = p₄  —  p₁ + d_A g h = p₂ + d_B g h  —  subtraindo membro a membro  —  p₂ – p₁ = (d_A – d_B) gh  —  como d_A > d_B  —  p₂ – p₁ > 0  —  p₂ > p₁.

(04) Errada  —  os pontos 5 e 6 estão no mesmo líquido e pertencem à mesma horizontal  —  logo, estão sob mesma pressão.

(08) Correta  —  embre-se que  —  E = d_líq V_imerso g  —  como d_B < d_A , num mesmo corpo totalmente imerso, o líquido B exerce menor empuxo.

(16) Correta  —  vide (02). 

R- (02 + 08 + 16) = 26

46- Dados  —  ρ_iceberg/ρ_água=0,90  —  A = 30 km²  —  h_emersa = 100 m  —  como o iceberg está em equilíbrio, a resultante de forças nele agindo (peso e empuxo) é nula.

E = P  — ρ_águaV_submerso g = ρ_icebergV g  —  V_submerso/V=ρ_iceberg/ρ_água=0,9  —   A.h_submersa/A(h_submersa + h_emersa)=0,9  —  h_submersa/(h_submersa + 100)=0,9  —  h_submersa   =   0,9 h_submersa + 90  —  0,1 h_submersa = 90  —  h_submersa= 900 m = 0,9 km  —  volume submerso  — 

V_submerso = Axh_submersa = 30×0,9  —  V_submerso = 27 km³. 

47- I. Errada  —  se colocado em água doce o ovo vai para o fundo, é porque ele é mais denso que ela  —  d_ovo > d_águadoce  —  d_águadoce < d_ovo  —   se na água salgada o ovo flutua  —  d_ovo < d_águasalgada  —  comparando as duas conclusões  —   d_doce < d_ovo < d_águasalgada.

II. Correta  —  o empuxo é igual ao peso de líquido deslocado.

III. Errada  —  a pressão não afeta, pois qualquer variação é transmitida integralmente em todas as direções a todos os pontos do líquido.   

R- B

48- Observe as figuras abaixo  —  d_a, a densidade da água  —  d_b, a densidade da bola  —   V, o volume da bola  —   V_o, o volume imerso da bola  —  na Fig. 1 o sistema está em repouso  —  o empuxo é igual ao peso da bola  —  E=P  —  d_agV_o=mg  —  d_aV_o=d_bV  —  d_b/d_a=V_o/V (I)  — 

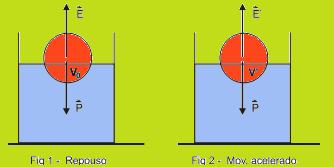
considere, agora, a Fig 2 para o caso do movimento ter aceleração vertical  —  para tal, vamos considerar a água um fluido incompressível e desprezar eventuais forças de viscosidade  —  considere, por exemplo, que a aceleração do elevador seja a para cima  —   camada de água em contato com o fundo do recipiente recebe desse fundo uma força normal  de intensidade  maior

que o peso, para haver aceleração  —  N – P = m a  —  N – m g = ma  —  N = m(a + g)  —  portanto, a pressão hidrostática no fundo do recipiente também aumenta, assim como em todos os pontos do líquido  —  ou seja, numa profundidade h a pressão hidrostática passa a ser  —  p = d_a (g + a) h  —  o empuxo ocorre pela diferença de pressão entre as faces superior e inferior do corpo, que é a própria pressão hidrostática  —  como pressão é o produto da força pela área  —  E’ = Δp.A  —  E’ = d_a(g + a).(h_i.A)  —  nessa expressão, h_i é a altura imersa do corpo e A é a área de atuação do empuxo  —  mas o produto (h_i.A) = ao volume imerso (V’)  —  dessa forma, para o corpo acelerando para cima, o empuxo é  —  E’ = d_aV’(g + a)  —   princípio fundamental da dinâmica  —  E’ – P = m a  —  d_aV’­(g + a ) – m g = m a  —  d_aV’­(g + a ) = d_bV(g + a)  —  d_b/d_a=V’/V (II)  — 

comparando (I) e (II), você conclui que V’ = V_o  —  se o elevador acelerasse para baixo, você obteria o mesmo resultado  —  assim, o volume imerso (V_o) independe da aceleração do elevador  —  R- E

49- Nos recipientes II e III, os volumes deslocados de água são iguais aos volumes das porções imersas de gelo e de bolas  —    volume imerso de gelo = volume de água deslocado pelo gelo  —  volume imerso de bolas = volume de água deslocado pelas bolas  —  VII  —  volume de água no recipiente II  —  VIII  —  volume de água no recipiente III  —  como nos três recipientes a água está no mesmo nível, nos recipientes II e III os volumes de água somados aos volumes imersos dão o mesmo volume de água (VI) contida no recipiente I  —  VII + Vgelo = VI  —   VIII + Vbolas = VI  —  o empuxo é igual ao peso do volume de água deslocado (E = d_água.V_desl.g)  —  recipiente I  —   PI = P_água = d_água.VI.g  —  recipiente II  —  PII = P_água + P_gelo  —  PII = d_água.VII.g  + d_água.V_gelo.g  —  PII = d_água.(VII + V_gelo).g  —  PII = d_água.VI.g  —  recipiente III  —  PIII = P_água + P_bola  —  PIII = d_água.VIII.g + d_água.V_bolas.g  —  PIII = d_água.(VIII + V_bolas).g  —  PIII = d_água.VI.g  —   PI = PII = PIII  —  R- E 

50- a) Dados: d_g = 0,920 g/cm³; d_água = 1,025 g/cm³ —  forças que agem sobre o cone de gelo  —  peso

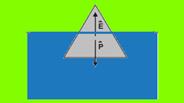
 e empuxo  —  a fração submersa  de volume do cone vale  —  f=V_subm/V_gelo  —  como ele está em equilíbrio E=P  —  d_água.V_imerso.g = d_gelo.V_gelo.g  — 

V_imerso/V_gelo = f=d_gelo/d_água  —  f=0,920/1,025  —  f=0,898  —  f=89,8%  —  se o cone fosse invertido, essa fração continuaria a mesma, pois o empuxo seria o mesmo, resultando na mesma equação do item anterior que mostra que a fração imersa depende apenas das densidades do gelo e da água, que são constantes.

b) Os fatores mencionados (variações da aceleração da gravidade e da pressão atmosférica) em nada afetam o experimento  —  a justificativa está na própria expressão encontrada no item anterior que mostra que a fração imersa depende apenas das densidades do gelo e da água, que independem das variações da pressão e da aceleração da gravidade.

51- a) A densidade é inversamente proporcional ao volume  —  o gráfico  mostra que quando a temperatura diminui, até 4 °C ocorre diminuição do volume, portanto um aumento da densidade  —  ou seja, quando a temperatura diminui correntes  de convecção  formam-se na água  —   a água da superfície se resfria, aumenta a densidade e desce, subindo a água que está no fundo  —  porém, quando a temperatura baixa de 4°C o volume começa a aumentar diminuindo a densidade, cessando o processo de convecção  —  assim, a água da superfície congela, e o gelo também é menos denso que a água, ficando na superfície  —  essa camada de gelo, que é um isolante térmico, impede a perda de calor da água que está abaixo para o meio ambiente.

b) T = 0,2 N  —  V = 1.000 cm³ = 10^-3 m³  —   d = 998 kg/m³  —   d’ = 1.000 kg/m³  —  na figura, a 20^oC –

equilíbrio  — P + T = E  —  P = d V g – T  —  P  = 998.10^-3.10  – 0,2  —  P = 9,98 – 0,2  —  P = 9,78 N  —  a 4°C  —  P + T’ = E’  —  T’ = E’ – P  —  T’ = d’ V g – P  —  T’ = 1.000.10^-3.10 – 9,78  —  T’= 10 – 9,78  —  T” = 0,22 N. 

52- V = 26 cm³ = 26.10^-6 m³  —   d = 10³ kg/m³  —   g = 9,8 m/s²  — E = d_liq.V_imerso.g  —  E = (10³).(26.10^-6).(9,8)  —  E = 0,2548 N  —   R- A

53- O empuxo é uma força vertical, para cima que o líquido exerce sobre um corpo nele imerso e é avaliado pelo princípio de Arquimedes: o empuxo tem a mesma intensidade do peso de líquido deslocado. 

R- B

54- Se o volume emerso é 1/8 do volume do corpo, o volume imerso é 7/8 desse volume  —  como o corpo está em equilíbrio, o peso e o empuxo têm a mesma intensidade  —  P=E  —  d_corpo.V_corpo.g=d_água.V_imerso.g  —  d_corpo/d_água=V_imerso/V_corpo  —  d_corpo/1=(7/8)V_corpo/V_corpo  —  d_corpo=7/8  —  d_corpo=0,875 g/cm³  —  R- B

55- P/E=12,5  —  E=P/12,5  —  princípio fundamental da dinâmica  —  F_R=ma  —  P – E = ma  —  mg – (mg/12,5) = ma  —  10 – 10/12,5=a  —  a=10 – 0,8  —  a=9,2m/s²  —  R- B

56- Veja figuras  —  a = 4 cm  —   dágua = 1 g/cm³  —  A_imersa = 0,7.A_total  —  Δh = 0,50 cm  —  a área

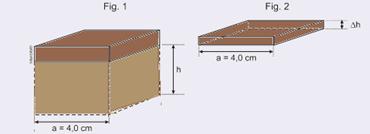
imersa é a área do fundo mais uma parte da área das 4 paredes laterais, de altura h  —  de acordo com o enunciado  —  A_imersa=0,7ª_total  —  a² + 4ah=0,7.6.a²  — 

4 h = 3,2 a  —  h = 0,8 a  —  como o cubo é um sólido reto e está em equilíbrio em água, seu peso é equilibrado pelo empuxo:

P = E  —  d_cubo.V_total.g = d_água.V_imerso.g  —  d_cubo/d_água=V_imerso/V_total  —  d_cubo/1=a²h/a³  —  d_cubo=a².0,8ª/a³ 

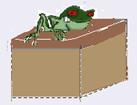
—  d_cubo=0,80 g/cm³   — o aumento do empuxo equilibra  o peso da rã  —  P_r=ΔE  —  mg=d_água.ΔV.g  —  m=d_água.A.Δh  —  m=1,0.16.0,5  —  m=8,0g  — 

R- E

 

57- I. Falsa  —  enunciado do princípio de Arquimedes: “Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido  para cima denominada de Empuxo, cuja intensidade  é igual ao peso do volume de líquido deslocado“

Características do empuxo:

Observe na expressão acima que a intensidade do empuxo (força para cima) é diretamente proporcional à densidade do líquido no qual ele está total ou parcialmente imerso  —  como a densidade da água do Mar Morto é maior que a do Mar Vermelho, a embarcação sofrerá maior empuxo no Mar Morto.

II. Correta  —  quanto maior a profundidade maior será a pressão e, quanto maior a pressão maior será a temperatura de ebulição da água  —  assim, o ponto de ebulição da água ao nível do Mar Morto é maior que o ponto de ebulição da água ao nível do mar que é de 100^oC=292^oF

III. Correta  —  pelo texto fornecido a diferença de altura entre o Mar Morto e o Mar Vermelho é de h=420m  —  W_P=

P.h=m.g.h=1000x10x420=4 200 000J.

IV. Falsa  —  a pressão hidrostática (devida somente à altura da coluna líquida) é fornecida por P_h=d_água.g.h  —  observe nesta expressão que, com g e h são os mesmos, ela depende apenas da densidade do líquido  —  será maior no Mar Morto porque aí a densidade da água é maior.

R- E.

 

58- Volume do cubo  —  V=0,1.0,1.0,1=10^-3m³  —  quando o cubo está no ar o dinamômetro no qual ele está suspenso pelo fio, a tração no mesmo é seu peso  — T= P=40N (figura 1)  —  quando ele se encontra com metade de seu volume imerso num líquido, ele recebe um empuxo, vertical e para cima, de intensidade  —  E=d_líq.g .V/2= d_líq.10.10^-3/2  —

E= d_líq.5.10^-3  —  nesse caso, a força de tração no fio é a indicação do dinamômetro de valor 

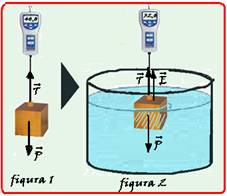
—  T=32N  —  como o bloco está em equilíbrio  —  P = T + E (figura 2)  —  40 = 32 + E  —  E=8N  —  8= d_líq.5.10^-3  —  d_líq=1,6.10³kg/m³= 1,6g/cm³  —  R- C.

59- Com o dinamômetro no ar, a indicação da força de tração no fio (indicação do dinamômetro) é igual ao peso do bloco  —  T=P=m.g=3.10  —  P=30N  —  quando o bloco é imerso na água, surge sobre ele um empuxo para cima, tornando-o mais leve (peso aparente) e, nesse caso, a força de tração T é a indicação do dinamômetro, ou seja, T=24N 

—  como o empuxo é o peso do volume de líquido deslocado (V’), que é igual ao peso da metade do volume (V) do corpo  —  volume do corpo V=ℓ³=(10^-1)³  —  V=10^-3m³  —  metade do volume  —  V’=(10^-3/2)m³  —  E=d_líquido.V’_{líquidodeslocado}.g  —  E=d_líquido.(10^-3/2).10  —  E=5.10^-3.d_líquido  —  como o bloco está em equilíbrio  —  P=T + E  —  30 = 24 + 5.10^-3.d_líquido  —  d_líquido=(6/5).10³=1,2.10³kg/m³  —  d_líquido=1,2kg/m³=1,2g/cm³  —  R- B.

60- Com o peixe totalmente imerso na água o módulo do empuxo (força vertical e para cima) é igual ao peso do volume do líquido deslocado — E= P_líquido=m_líquidog  —  d_líquido=m_líquido/V  — 

  m_líquido=d_líquido.V_líquido  —  E=d_líquido.V_líquido.g  —  onde  — Analisando as alternativas:

a) Falsa  —  observe na expressão E=d_líquido.V_líquido.g que o empuxo E é diretamente proporcional ao volume de líquido deslocado que é igual ao volume do peixe.

b) Falsa  —  como a massa não varia o peso também não variará, pois, P=m.g (m e g são constantes)

c) Falsa  —  a densidade da água é a mesma, próximo ou não do peixe.

d) Falsa  —  quando enche a bexiga natatória de gases, o volume do peixe aumenta sem variar sua massa m  —  assim, a densidade do peixe diminui, pois d=m/V (observe nesta expressão que d é inversamente proporcional a V, pois m é constante)

e) Correta  —  o módulo da força peso da quantidade de água deslocada pelo corpo do peixe aumenta, pois esse módulo é igual ao empuxo E.

61- Considere que o ar se comporta como um gás ideal e note que o número de moles de ar no interior do balão é proporcional à sua densidade.

a) Volume do balão  —  1 L=1 dm³=10^-3 m³  —  V=3.10⁶.10^-3  —  V=3.10³ m³  —  cálculo do empuxo (força vertical, para cima e de intensidade E= ρ_amb.V.g) do balão  —  E= ρ_amb.V.g=1,26.3.10³.10  —  E=3,78.10⁴ N.

b) Equação geral dos gases perfeitos  —  P.V=n.R.T  —  P.V=(m/M).R.T  —  o enunciado afirma que durante a transformação a pressão P e o volume V permanecem constantes  —  P.V=constante, então (m/M).R.T=constante  —  como M e R já são constantes, então o produto da massa m pela temperatura T  também será constante  —  m.T=constante  —  observe que o enunciado afirma que número de moles de ar no interior do balão é proporcional à sua densidade, o que implica que a massa m também será proporcional à densidade ρ.T=constante  —  ρ_amb.T_amb = ρ_quente.T_quente  —  1.26.300 = 1,05.T_quente  —  T_quente=360K.

62- Se um corpo estiver flutuando parcialmente imerso num líquido, a força resultante sobre ele é

nula (equilíbrio vertical) —  P = E   — P=d_c.V_total.g  —  E=d_líquido.V_imerso.g  — P = E  —  d_c.V_total.g=d.V_imerso.g  —  d_corpo/d_líquido=V_imerso/V_total  —  cálculo do raio do tronco  —  perímetro=2.π.R  —  1,2=2.3.R  —  R=0,2m  —  volume total do tronco  —  V_total=π.R²=3.(0,2)²  —  V_total=0,36m³  —  densidade do tronco  —  d_corpo=0,8.10³kg/m³  —  d_líquido=1,0.10³kg/m³  —  d_corpo/d_líquido=V_imerso/V_total  — 0,8.10³/1,0.10³=0,36/V_imerso  —  V_imerso=0,288m³  —  R- B

63- Considerando a carga totalmente imersa na água ela sofrerá um empuxo (força vertical e para cima) de intensidade  —  E=d_água.V_carga.g  —  E=(1,0.10³kg/m³).(20.10^-3m³).(10m/s²)  — E=200km/s²=200N  —  peso da carga (vertical e para baixo de intensidade  —   P=mg=50.10  —   

  P=500N  —  sobre a carga agem para cima duas forças de tração (2T) aplicadas pela corda  —  sendo a ascensão com velocidade constante a força resultante sobre a carga é nula  —  F_R=0  —  P=E + 2T  —  500=200 + 2T  —  T=150N  —  R- D

64- a) A força que o ar exerce sobre o balão corresponde ao empuxo (força vertical e para cima) cuja intensidade é o peso do volume de ar deslocado pelo balão (que é o próprio volume do balão) e fornecido por  —  E=ρ_ar.V_balão.g=1,3.0,5.10  —  E=6,5N.

b) Dado do exercício  —  volume máximo do balão  —  V_b=0,5m³  —  o balão contém hélio  —  ρ_He=0,18kg/m³  — 

ρ_He=m_He/V_b  —  0,18=m_He/0,5  —  m_He=0,09kg.

c) Veja figura abaixo:

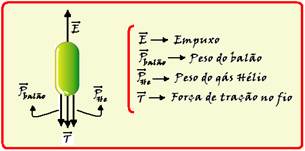
d) Estando o sistema em equilíbrio, a força resultante sobre o balão é nula  —   T + P_balão + P_He = E  —  T + m_balão.g +

ρ_He.V_balão.g = E  —  T + 0,1.10 + 0,18.0,5.10 = 6,5  —  T=4,6N.

65- Empuxo  —  “Todo corpo imerso num líquido recebe uma força para cima que é igual ao peso do volume do líquido deslocado”  —  o volume do líquido deslocado corresponde a 3/4 do volume do cilindro (parte imersa)  —  V_L=(3/4).S.h=(3/4).(400.10^-4).  (12.10^-2)  —  V_L=36.10^-4m³  —  E= ρ_L.V_L.g=(0,8.10³).36.10^-4.10  —  E=28,8 N  —  peso do cilindro  —  P_cilindro= mg   —  P_cilindro=d_cilindro.V_cilindro.g=  —   P_cilindro=d_cilindro.(S.h).g= d_cilindro.(400.10^-4).12.10^-2.10  —  P_cilindro= d_cilindro.48.10^-3  —  como o cilindro encontra-se em equilíbrio  —  E = P  —  28,8 = 48.10^-3. d_cilindro  —  d_cilindro=28,8/48.10^-3  —  d_cilindro=0,6.10³kg/m³=0,6.10³.10^-3 — 

d_cilindro=0,6g/cm³  —  R- D

66-Todo corpo imerso em um líquido recebe uma força vertical e para cima denominada Empuxo que obedece à seguinte equação  —E=densidadedolíquidoxvolumedelíquidodeslocadoxaceleraçãodagravidade  — observe que, quanto maior a densidade do líquido, no caso do mar morto (alta concentração salina), maior será a força do empuxo para cima e com mais facilidade ele flutua  —  R- B.

 

Voltar para os exercícios