Princípio de Pascal e Prensa hidráulica – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Princípio de Pascal e Prensa hidráulica
01- Princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal:
“ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido” — R- E
02- Veja o esquema de um freio hidráulico na figura abaixo;
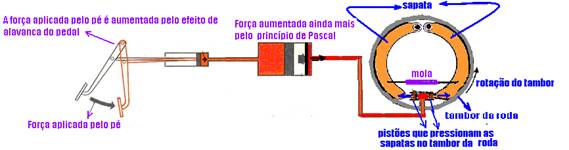
R- A
03- A pressão é a mesma em todos os pontos, inclusive em cada cilindro (Princípio de Pascal) — R- C
04- Força. A força que age na roda é muito maior do que aquela aplicada no pedal (Princípio de Pascal), devido à diferença de área entre os êmbolos e também devido ao sistema de alavancas do pedal do freio.
05- Sendo a pressão em cada êmbolo a mesma — F1/A1=F2/A2 — F2/F1=A2/A1 — R- E
06- F1/S1=F2/S2 — F1/S1=F2/4S1 — F2=4F1 — como o sistema está em equilíbrio — F2=4F1=P — veja nas figuras
abaixo que o trabalho realizado por F1 para o êmbolo menor descer é o mesmo realizado por F2 para o êmbolo maior subir — W=F1.h1=F2.h2 — se o trabalho realizado é o mesmo, a energia mecânica do sistema se conserva — R- B
07- a) Estando o êmbolo maior em equilíbrio, a força aplicada pelo líquido sobre ele, equilibra o peso do automóvel — F=p=mg=3.103.10 — p=3.104N — a pressão exercida pelo cilindro é a mesma que a exercida pelo êmbolo P=F/S=p/S=3.104/6.10-3 — P=0,5.107 — P=5.106N/m2
b) O volume de líquido expulso pelo cilindro ao descer h1 é o mesmo que faz o êmbolo subir h2 — S1.h1=S2.h2 — 3.10-5.h1=
6.10-3.0,2 — h1=12.10-4/3.10-5 — h1=4.10 — h1=40m=4.000cm — (a válvula impede o retorno do líquido, fazendo com que esse deslocamento corresponda a muitos “vai e vem” do pistão)
08- Peso do caminhoneiro — p=mg=80.10 — p=800N=F1 — F1/S1=F2/S2 — 800/πR12 = F2/πR22 —
800/π(5.10-3)2=F2/π.(3.10-2)2 — F2=28.800N — massa dessa carga — p=mg — 28.800=m.10 — m=2.880kg — R- A
09- F1/A1=F2/A2 — 2/π(5.10-3)2=F2/π(1.10-2)2 — F2=2.10-4/25.10-6 — F2=0,08.102 F2=8N — essa força equilibra uma massa — p=Mg — 8=M.10 — M=0,8kg=800g — R- B
10- L e M — P/A=PM/2A — PM=2P — L e N — P/A=PN/3A — PN=3P — R- A
11- A2=8.A1 — F/A1=400/8.A1 — F=50N
12- Como as unidades são as mesmas e estão, na equação, em cada lado da igualdade, não é preciso transformá-las em m2 — mA.g/a=mB.g/b — 4/80=mB/20 — mB=1kg — R- C
13- F1/π(d1/2)2=F2/π(R2)2 — 100/π(0,05/2)2=10.000/π(R2)2 — 100/0,0625=10.000/(R2)2 — R2=√6,25 — R2=2,5m — d2=5,0m — a pressão é a mesma nos dois êmbolos e vale — P=10.000/π(6,25) — P=10.000/3,1416.6,25 — P= — P=509,3Pa — R- C
14- independe da unidade — A1=50 — P=F1/A1=F1/50 — A2=2 — P=F2/A2=30/2=15 — F1/50=
15 — F1=750N — R- E
15- dP=30dF — Velocidade constante — equilíbrio dinâmico — FP=pP=m.g — FPdP=30dF — FP/SP=FF/SF — m.g/π(dP/2)2=F/(dF/2)2 — 9.000×10/(30dF)2=F/(dF)2 — 90.000/900=F — F=100N — R- A
16- FA/SA=FB/SB — FA/πD2=FB/π(4D)2 — FA/1=FB/16 — FA/FB=16
17- 200/25=F/2.000 — F=p=400.000/25 — F=p=16.000N
18- F1/S1=F2/S2 — 1200/(S2/2)=F2/S2 — F2=F3=400N — R- B
19- Força (F1) ampliada pelo sistema de articulações quando no pedal é aplicada a força F=50N —
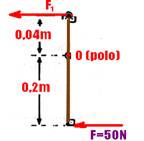
colocando o pólo O na articulação central e lembrando que a soma dos momentos das forças em relação ao pólo é nula — – F.d1 + F1.d2=0 —
– 50.0,2 + F1.0,04=0 — F1=250N — essa força é transmitida até o êmbolo 1 de área S1=40mm2=4.10-5m2 que está ligado, por meio de vaso comunicante até o êmbolo 2 de área S2=80mm2=8.10-5m2 — aplicando o teorema de Pascal
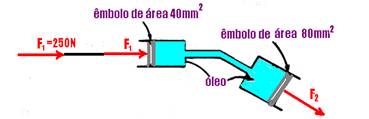
nos êmbolos 1 e 2 — F1/S1=F2/S2 — 250/4.10-5=F2/8.10-5 — F2=500N — R- E
20- Colocando o pólo no ponto fixo, calculando o momento de cada força em relação à ele e
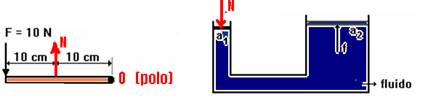
igualando a zero — – 10.0,2+ 1N.0,1=0 — N=20N — aplicando o teorema de Pascal — N/a1=F/5.a1 — 20/1=F/5 — F=100N — R- D
21- Qualquer acréscimo de pressão efetuado em um ponto de um fluido em equilíbrio é transmitido integralmente aos demais pontos desse líquido — Teorema de Pascal — R- A
22- Dados — F1 = 4.000 N — A1 = 10 cm2 — A2 = 0,05 cm2 — L = 1 m — m = 1 g = 10-3 kg
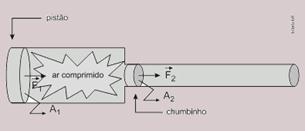
quando você aplica a força 
sobre o pistão de área A1, através do ar comprimido, transmite-se sobre o chumbinho de área A2, a força 
— a relação entre essas grandezas é dada pelo princípio de Pascal — F1/A1=F2/A2 — 4.000/10=F2/0,05 — F2=20N — essa força , também suposta constante, realiza trabalho sobre o chumbinho ao longo do cano da espingarda, aumentando sua velocidade a partir do repouso (vo = 0) — pelo teorema da energia cinética, considerando como a força resultante sobre o chumbinho — WF2=ΔEcin — F.L=mV2/2 — 20.1=10-3.V2/2 — V=200m/s — R- B
23- a) Alavanca inter-resistente – a força transmitida localiza-se entre o pólo (parte inferior do pedal) e a força aplicada pelo operador (parte superior do pedal).
b) Princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal:
“ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido” — A maioria dos sistemas multiplicadores de forças é baseado no princípio de Pascal e, para explicá-lo considere um líquido ideal no interior de dois cilindros verticais de seções diferentes e interligados. Esses cilindros, em contato com a parte superior do líquido, possuem dois êmbolos de áreas S1 e S2.
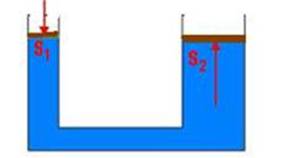
Uma força de intensidade F1 aplicada ao êmbolo de menor área (S1), provocará um aumento de pressão dado por ΔP=F1/S1 e, pelo princípio de Pascal esse acréscimo de pressão se transmitirá integralmente a todos os pontos do líquido e das paredes, inclusive para o êmbolo de maior área (S2). Então, o êmbolo maior fica sujeito a uma força F2, tal que ΔP=F2/S2. Pelo princípio de Pascal essa variação de pressão se transmite integralmente do êmbolo menor ao êmbolo maior e são iguais — F1/S1=F2/S2.
c) No pedal — MF1=+F1.d1= + 100.0,4=40N.m — MF2= – F2.d2= – 0,2F2 — a soma dos momentos de cada força deve ser nula — 40 – 0,2F2=0 — F2=200N — esta força é transmitida até o pistão 1, que através do Princípio de
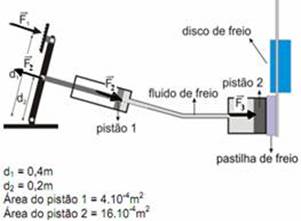
Pascal, a aumenta para F3 no pistão 2 — F2/S2=F2=3/S3 — 200/4.10-4 = F3/16.10-4 — F3=800N (força aplicada na pastilha do freio)
24- Seja F a força aplicada pelo motorista no pedal — pelo enunciado a alavanca tem a
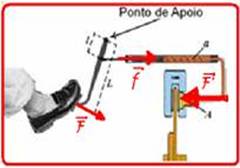
capacidade de ampliação da força aplicada por um fator igual à razão direta de seus braços, que é de 40/10=4 vezes — f=4F — a prensa hidráulica amplia a força f na razão direta de suas áreas, ou seja, de 8 vezes — F’=8f — F’=8.4F — F’=32F — R- A.