Experiência de Torricelli e Vasos comunicantes com líquidos imiscíveis em equilíbrio – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Experiência de Torricelli e Vasos comunicantes com líquidos imiscíveis em equilíbrio
01- a) São bolhas de ar que é expulso do interior do vidro do conta-gotas.
b) Com o ar expulso, a pressão interna diminui e a maior pressão externa empurra o líquido para dentro.
02- O ar no interior da sanfona e no interior do bulbo de vidro e em contato com a superfície do líquido está igualmente concentrado (igualmente denso) e suportam a mesma pressão (P1=P2) — como 2 (no bulbo de vidro) e 3 (no tubo) estão no mesmo nível, suportam também a mesma pressão (P1=P2=P3) — no tubo , P3>P4, pois 3 suporta maior altura de coluna líquida que 4 — R- C
03- I- Falsa, será menor, pois no alto da montanha a pressão é menor.
II- Correta – veja teoria
III- Correta – veja teoria
04- A alternativa incorreta é a D, pois com a boca da garrafa totalmente tampada a água não jorrará por nenhum dos dois orifícios, pois a pressão externa é maior que a interna — R- D
05- À medida que os sacos sobem sobe seu volume vai aumentando porque a diferença entre a pressão do ar dentro dos sacos e a pressão cada vez mais reduzida fora dela gera uma força resultante que empurra o plástico da bexiga para fora — R- B.
06- Cálculo do valor da pressão atmosférica em Brasília — P=dHg.g.h=13,6.103.9,8.0,67
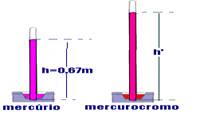
— P=8,9.104N/m2 (Pa) — Essa pressão, em Brasília (P=8,9.104N/m2), quando medida com mercurocromo de densidade dmc=0,99.103kg/m3) equivalerá à uma altura de — P=dmc.g.h’ — 8,9.104=0,99.103.9,8.h’ — h’=8,9.104/9,702.103 — h’=0,92.101 — h’=9,2m=92dm
07- Quanto maior a altitude, menor é a pressão e quanto menor a pressão menor é a temperatura de ebulição da água —
R- A
08- A pressão ao nível do mar corresponde à pressão devida a altura da coluna de ar — Patm=dar.g.h — 1,0.105=1,3.103.10.h — h=78.102m=7,8.103m=7,8km — R– C
09- Ao nível do mar o barômetro de mercúrio equilibra uma coluna de 76cm de Hg — como a pressão diminui de 1cm de Hg a cada 100m, na altura de 900m a coluna de mercúrio diminuirá de 9cm e, terá uma altura de P=76-9=67cmHg — sendo a densidade do líquido 4 vezes menor que a do mercúrio, ela equilibrará uma altura 4 vezes maior de líquido —
P=67 x 4=268cm de líquido — P=2,68m de líquido — R- C
10- V=4m.5m.3m=60m3 — d=m/V — 1,2=m/60 — m=72kg — P=mg=72.10 — P=720N — R- A
11- Observe na figura abaixo que a pressão na superfície da água (ponto Q) é a mesma que aquela devido à altura da coluna
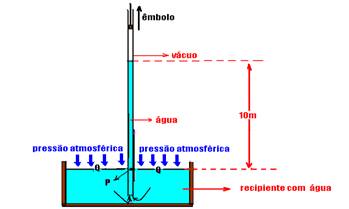
de água (ponto p) — PQ=Pp — densidade dágua=103kg/m3 e g=9,8m/s2 — PQ= Patm — Pp==dágua.g.hágua — 1,01.105=103.9,8.hágua — hágua=10,3m — portanto, a pressão atmosférica equilibra uma coluna de água de altura aproximadamente 10m e, essa pressão não consegue empurrar qualquer coluna de água a uma altura superior a 10m
12- a) Na Lua não existiria atmosfera que exerceria pressão sobre a coluna de mercúrio, de modo que a coluna não subiria.
b) Pplaneta=dHg.1g/2,5.h — 1,0.105/10=13,6.103.10/2,5.h — h=1,0.104/54,4.104 — h=0,0184m — h=184mm
13- a) dágua.g.10=dvinho.g.15 — dágua/dvinho=1,5
b) menor que 15m — valor compreendido entre 10m e 15m, dependendo da quantidade de água acrescentada ao vinho
14- Todos os pontos da superfície livre do café estão submetidos à mesma pressão e consequentemente possuem o mesmo nível horizontal em relação à linha de referência do sistema — R- C
15- Todos os pontos que se encontram na mesma linha horizontal (altura, profundidade)estão submetidos à mesma pressão — R- B
16- pA=pB (mesmo nível) — o gás pressiona mais o líquido que a pressão atmosférica pó — pg > po — R- C
17- O líquido 2 é mais denso e deve ficar na parte inferior dos vasos — R- A
18- Observe que PB é maior que PA (pressiona mais a coluna de água) e PC é menor que PA(pressiona menos a coluna de água) — R- D
19- A pressão nos pontos M e N é a mesma — PM=PN — Patm + dX.g..18=Patm + dX.g.10 + dy.g.10
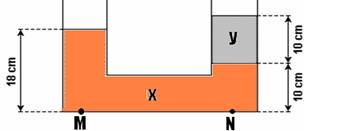
— 18.dX=10.dY +10.dX — 8dX=10dy — dY/dX=8/10=0,8 — R- A
20- a) A pressão do gás no botijão é a mesma que no ponto A (PA=Pgás), que por sua vez é a mesma
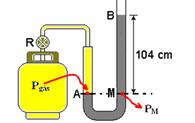
que no ponto M —Pgás=PM — Pgás=Patm + dHg.g.h=105 + 13,6.103.10.1,04 — Pgás=105 + 14,44.104 — Pgás=1,0.105 + 1,44.105 — Pgás=2,44.105 Pa
b) Em a — Pgás=F/S — 2,44.105=F/2.10-4 — F=48,8N
21- a) A pressão nos pontos M e N da figura é a mesma — PM=PN — Patm + dB.g.0,8 = Patm +
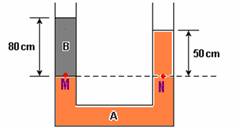
dA.g.0,5 — 0,8.dB =0,5.dA — 0,8.dB=0,5.2.103 — dB=103/0,8 — dB=1,25.103kig/m3
b) PM= Patm + dB.g.0,8=1,0.105 + 1,25.103.10.0,8 — PM=PN=1,0.105 + 10.103=1,0.105+ 0,1.105 — PM=PN=1,1.105Pa
22- Pressão causada pelo petróleo, Patm não participa — PA=PB — PB=dB.g.h= 1,0.103.10.4.10-2= 40.10 — PA=PB=400Pa —
R- B
23– PM=PN — Patm + ρB.g.h = Patm + ρA.g.0,75h
ρB=0,75ρA — ρB/ρA=0,75 — R- A
24- Vl=500mL=500.10-3L=500.10-3dm3=500.10-3.10-3m3 — Vl=5.10-4m3 — Vl=S.h — 5.10-4=S.h
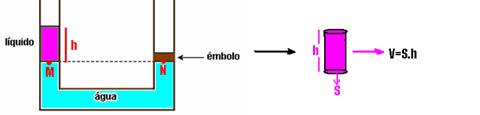
— h=5.10-4/S — dl=0,8.103 — dl=8.102kg/m3 — PM=Patm + dl.g.h= Patm + 8.102.10.5.10-4/S — PM=Patm + 4/S — PN=Patm + Pêmbolo — PN=Patm + F/S=Patm + p/S — PN=Patm + p/S — PM=PN — Patm + 4/S=Patm + p/S — p=4N
25- a) Observe na última coluna que o produto PxV é praticamente constante (Lei de Boyle para transformações isotérmicas)
b) Supondo que cada 8 unidades tenha 0,5cm — regra de três — 8u – 0,5m — 24u – h — h=1,5m — P=Po + dgh=1,0.105 + 14.103.10.1,5 — P=3,1.105N/m2(Pa)
26- Sendo a seção reta circular (S=1,0.10-4m2) no diafragma a mesma, e como a densidade do líquido A é maior que a do líquido B, a intensidade da força resultante sobre o diafragma vale — FR=FA – FB — PA=FA/S — FA=PA.S — FB=PB.S — FR=PA.S – PB.S=S(PA – PB) — FR=S.(dA.g.h – dB.g.h)=1,0.10-4.(5.103.10.0,1 – 0,5.103.10.0,1)=
1,0.10-4.4,5.103 — FR=4.500.10-4 N
27- Observe a figura abaixo, onde os pontos R e S estão no mesmo nível e suportam a mesma
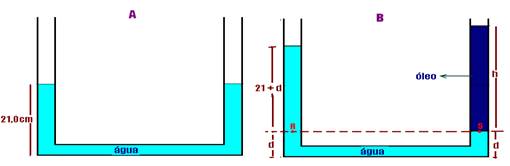
pressão — PR=PS — PR=Patm + dágua.g.(21 + d) — PS =Patm + dóleo.g.h — PR=OS — Patm + dágua.g.(21 + d)= Patm + dóleo.g.h — dágua.(21 + d)= dóleo.h — observe que h + d=42 — d=42 – h — dágua.(21 + 42 – h)=dóleo.h — 1.63 – 1.h=0,8h — 1,8h=63 — h=63/1,8 — h=35cm — R- D
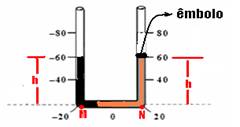
28- a) As pressões exercidas pelos líquidos I e II no fundo do tubo (pontos M e N) são iguais — PM=PN — Po + dI . g . hI = Po + dII . g . hII — 1800 . g . 0,20 = dII . g . 0,60 — dII = 600 kg/m3
b) Nos pontos compreendidos entre -80cm até -40cm a pressão é constante e é a atmosférica de valor Po=105N/m2 — np ponto 80cm a pressão também é a atmosférica de valor Po=105N/m2 — nos pontos de abscissas -20cm até + 20cm a pressão é constante e vale — P-20=Patm + dI.g.hI= 105 + 1800.10.0,20=1,036.105 N/m2 — de -20cm até + 20cm – P=1,036.105N/m2 — entre esses valores a variação é linear (reta inclinada) — veja gráfico abaixo
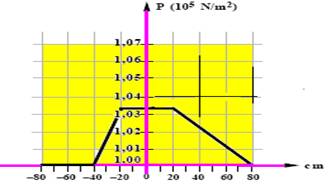
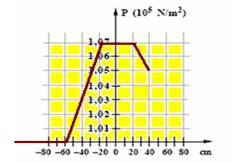
c) Para que os níveis dos líquidos se igualem, a superfície livre do líquido I deve subir 20cm, estacionando na abscissa
-60cm e a do líquido II descer 20cm, estacionando na abscissa +60cm — nos pontos M e N a pressão é a mesma e, no ponto M vale — PM=Patm + dI.g.h=105 + 1.800.10.0,40=105 + 0,072.105 — PM=PN= 1,072.105N/m2 — pressão no ponto de abscissa +60cm — PN=P+60cm + dII.g.h — 1,072.105=P+60cm + 600.10.0,40 — P+60cm=1,072.105 – 0,024.105 — P+60cm=1,048.105N/m2 — gráfico abaixo
29- a) Na figura II, na extremidade do orifício de altura h1=2,0m a pressão que atua é a pressão atmosférica Po=1,0.105N/m2 — Po=dgh1 + P1 — 1,0.105=1,0.103.10.2,0 + P1 — P1=1,0.105 – 2,0.104 — P1=8,0.104N/m2
b) Chamando de S a área da base do tanque — lei geral dos gases perfeitos — Po.Vo/To=P1.V1/T1 — 1,0.105.S(6,0 – ho)/300 = 8,0.104.S.(6,0 – 2,0)/360 — ho=10/3 m=3,3m
30- PM=Pgás=PN — PN=Patm + dgh=76cmHg + 30cmHg —
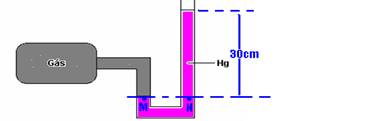
Pgás=106cmHg — R- D
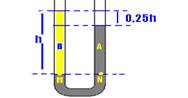
31- PM=Patm + ρA.g.h — PN=Patm + ρB.g (h – 0,25h) — PM=PN — Patm + ρA.g.h=Patm+ ρB.g.(h-0,25) — ρA.h= ρB.(h-0,25h) — ρA.h= ρB.0,75h — ρB/ρA0,75 — R- A
Para que o óleo escoe com facilidade da lata, você deve fazer dois furos na mesma, um para que a pressão atmosférica empurre o óleo para fora da lata e o outro para que o óleo saia da mesma.
32- a) O escoamento do líquido se interrompe quando a pressão no fundo do recipiente se iguala à pressão no bico da torneira, que é a pressão atmosférica po — chamando de p a pressão exercida sobre a superfície livre do líquido nesta situação — pelo teorema de Stevin — po = p + ρg H — Po – P=ρgH — ΔP=ρgH
c) Como a pressão atmosférica diminui com a altitude, a cidade localizada à maior altitude é aquela na qual é menor a pressão atmosférica — a cidade B
33- a) Falsa — uma bomba de sucção é uma bomba que retira o ar de sua extremidade superior, produzindo o vácuo — com ar expulso,a pressão interna diminui e a maior pressão externa empurra o líquido para cima — isso ocorre independente da espessura dos canos e da potência do motor que produz a sucção (vácuo).
b) Correta — Se a experiência de Torricelli for realizada ao nível do mar, mas com água, cuja densidade é 13,6 vezes menor que a do mercúrio, a altura da coluna de água será aproximadamente igual a 10,3m.
c) Falsa — veja justificativa a.
d) Falsa — veja justificativa b.
e) Falsa.
R- B
34- a) O líquido só vai parar de escoar pela torneira quando a pressão (Po) em todos os pontos do fundo do recipiente for igual à

pressão na ponta da torneira que está aberta e essa pressão é a pressão atmosférica (Po) — isso ocorre porque todos os pontos de mesmo nível de altura (mesma horizontal) suportam a mesma pressão (teorema de Stevin) — chamando de P a pressão na interface ar-líquido e de Po(pressão atmosférica) a pressão na parte inferior do líquido, pelo teorema de Stevin — Po = P + ρ.g.H — P= Po – ρ.g.H.
b) Veja a figura abaixo que mostra a pressão e o volume do ar contido no recipiente antes e depois do volume ∆V de água ser
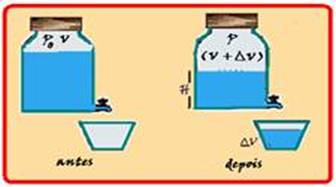
transferido — numa evolução isotérmica a temperatura é constante (To = T) — Po.Vo/To = P.V/T — Po.V = P.(V + ∆V) — P=Po.V/(V + ∆V).
c) Observe no gráfico que a menor pressão atmosférica (Po=ρ.g.H) é a da cidade B — como a pressão atmosférica diminui com a
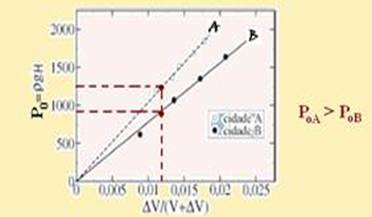
altitude,quanto menor a pressão atmosférica maior é a altitude da cidade — a cidade B está numa altitude maior.
