Velocidade de Escape – Exercício
Exercícios de vestibulares sobre
Velocidade de Escape
01-(UFBA) Sabemos que a velocidade de escape da Terra é aproximadamente 11km/s.

Entretanto, quando observamos o lançamento de um foguete, é fácil perceber que sua velocidade nos instantes iniciais é muito inferior a este valor. Por quê?
02-(UFB) O diâmetro médio da Terra é, aproximadamente, 2,6 vezes maior que o de Mercúrio. A massa de Mercúrio é 0,55 da massa da Terra. Calcule a razão entre a velocidade de escape na Terra (VeT) e a velocidade de escape em Mercúrio (VeM).
03-(UFB) Suponha que exista um planeta cuja massa seja cuja massa seja 4 vezes maior que a massa da Terra e cujo raio seja 4 vezes menor que o raio da Terra. Calcule a relação entre a velocidade de escape no Planeta e a velocidade de escape na Terra.
04-(UFB) Considere um satélite em trajetória elíptica ao redor de um planeta. Qual é a relação entre suas energias cinética, potencial e mecânica quando o satélite estiver:
a) no afélio (apogeu)?
b) no periélio ( perigeu)?
05-(UFB) Com relação ao exercício anterior, o que aconteceria com essas energias se a órbita do satélite fosse circular?
06-(Uesb)- A aceleração da gravidade na superfície de um asteróide é igual a 3,0m/s2. Se o raio do asteróide é igual a 500,0km, então, para que um foguete escape da atração gravitacional desse asteróide, ele deve ser lançado da sua superfície com uma velocidade, em km/s, de
![]()
07-(UFAL-AL) Uma partícula é lançada verticalmente para cima a partir da superfície da Terra, atingindo uma altura máxima (em relação ao ponto de lançamento) igual ao próprio raio da Terra, RT. Desprezando os atritos e o movimento de rotação terrestre, e denotando a aceleração da gravidade na superfície da Terra por g, com que velocidade a partícula foi lançada?
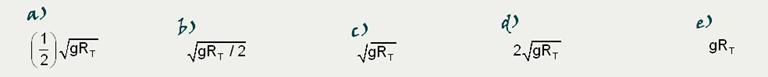
08-(UERJ-RJ) LEIA AS INFORMAÇÕES A SEGUIR PARA A SOLUÇÃO DESTA QUESTÃO.

Buracos negros são corpos celestes, em geral, extremamente densos. Em qualquer instante, o raio de um buraco negro é menor que o raio R de um outro corpo celeste de mesma massa, para o qual a velocidade de escape de uma partícula corresponde à velocidade c da luz no vácuo.
Determine a densidade mínima de um buraco negro, em função de R, de c e da constante G.
