Satélites em órbitas circulares – Exercícios
Exercícios de vestibulares sobre
Satélites em órbitas circulares
01-(UNICAMP-SP) Observações astronômicas indicam que as velocidades de rotação das estrelas em torno de galáxias são incompatíveis com a distribuição de massa visível das galáxias, sugerindo que grande parte da matéria do Universo é escura, isto é, matéria que não interage com a luz. O movimento de rotação das estrelas resulta da força de atração gravitacional que as galáxias exercem sobre elas.
A curva no gráfico abaixo mostra como a força gravitacional F=GMm/r2que uma galáxia de massa M exerce sobre uma estrela externa à galáxia, deve variar em função da distância r da estrela em relação ao centro da galáxia, considerando-se m=1,0.1030 kg para a massa da estrela. A constante de gravitação G vale
106,7.-11 m2.F/kg-2.
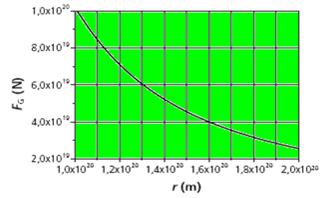
Calcule a velocidade de uma estrela em órbita circular a uma distânciar=1,6×1020 m do centro da galáxia.
02-(UFRS) O cometa de Halley atingiu, em 1986, sua posição mais próxima do Sol (periélio) e, no ano de 2023, atingirá sua posição mais afastada do Sol (afélio).
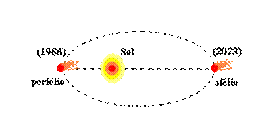
Assinale a opção correta:
a) Entre 1986 e 2023 a força gravitacional que o Sol aplica no cometa será centrípeta
b) Entre 1986 e 2023 o cometa terá movimento uniforme
c) No ano de 2041 a energia potencial do sistema Sol-cometa será máxima
d) Ao atingir o afélio, no ano de 2023, a energia potencial gravitacional do sistema Sol-cometa será máxima
03-(INATEL-MG) Um satélite permanece em órbita circular terrestre de raio R com velocidade tangencial V. Qual deverá ser a velocidade tangencial desse satélite para permanecer em órbita circular lunar de mesmo raio R? Considere a massa da Lua 81 vezes menor que a massa da Terra.
04-(UNICAMP-SP) Um míssil é lançado horizontalmente em órbita circular rasante à superfície da Terra. Adote o raio da Terra R=6400km, massa da Terra M=6,0.1024 kg, a constante de gravitação G=6,7.10-11 Nm2/kg2 e, para simplificar, tome 3 como valor aproximado de p.

a) Qual é a velocidade de lançamento?
b) Qual é o período da órbita?
05-(FUVEST-SP) Se fosse possível colocar um satélite em órbita rasante em torno da Terra, o seu período seria T. Sendo G a constante de gravitação universal, expresse a massa específica (densidade média) da Terra em função de T e G.
06-(UF-ES) Dois satélites descrevem órbitas circulares em torno da Terra.

O raio da órbita do satélite mais afastado da Terra é o dobro do raio da órbita do satélite mais próximo. Considere que Va e Vf são, respectivamente, os módulos das velocidades do satélite afastado e do satélite próximo. A relação entre esses módulos é:
![]()
07-(UF-MG) Dois satélites artificiais, R e S, estão em órbitas circulares de mesmo raio, em torno da Terra.
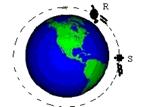
A massa do satélite R é maior que a do satélite S. Com relação ao módulo das velocidades, VR e VS, e dos períodos de translação, TR e TS, pode-se afirmar que:
a) VR < VS e TR = TS
b) VR < VS e TR > TS
c) VR = VS e TR =TS
d) VR = VS e TR > TS
e) VR > VS e TR > TS
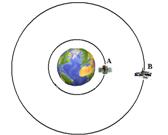
08-(CESGRANRIO-RJ) Dois satélites, A e B, giram ao redor da Terra em órbitas circulares. O raio da Terra é R e as alturas das órbitas dos satélites, em relação à superfície terrestre, são, respectivamente, HA=R e HB=3R. Sendo aA e aB os módulos das acelerações vetoriais dos satélites em órbita, então é correto afirmar que:
![]()
09-(FUVEST-SP) Um satélite artificial se move em órbita circular ao redor da Terra, ficando permanentemente sobre a cidade de Macapá. Qual é o seu período?
10-(FUVEST-SP) Satélites utilizados para telecomunicações são colocados em órbitas geo-estacionárias ao redor da Terra, ou seja, de tal forma que permaneçam sempre acima de um mesmo ponto da superfície da Terra. Considere algumas condições que deveriam corresponder a esses satélites:
I. Ter o mesmo período, de cerca de 24 horas.
II. Ter aproximadamente a mesma massa.
III. Estar aproximadamente à mesma altitude.
IV. Manter-se num plano que contenha o círculo do equador terrestre.
O conjunto de todas as condições que satélites em órbitas geo-estacionárias devem necessariamente obedecer corresponde a:
a) I e III
b) I, II e III
c) I, III e IV
d) II e III
e) II e IV
11-(UFG) Considere que a Estação Espacial Internacional, de massa M, descreve uma órbita elíptica estável em torno da Terra, com um período de revolução T e raio médio R da órbita. Nesse movimento,
(A) o período depende de sua massa.
(B) a razão entre o cubo do seu período e o quadrado do raio médio da órbita é uma constante de movimento.
(C) o módulo de sua velocidade é constante em sua órbita.
(D) a energia cinética é máxima no afélio.
(E) a energia cinética é máxima no perigeu.
12-(UPE-PE) A figura a seguir representa a trajetória de duas estrelas idênticas (cada uma com

massa M) que giram em torno do centro de massa das duas estrelas. Cada órbita é circular e possui raio R, de modo que as duas estrelas estão sempre em lados opostos do círculo. Considere G a constante de gravitação universal.
Analise as proposições que se seguem.

soma dos números entre parênteses das proposições que corresponde aos itens corretos é igual a
![]()
13-(FGV-RJ) Muitos satélites utilizados em telefonia, transmissões de rádio e TV, internet e outros serviços de telecomunicações ocupam a órbita geoestacionária. Nesta órbita, situada no plano da
linha do equador, os satélites permanecem sempre acima de um mesmo ponto da superfície terrestre, parecendo parados para um observador no equador. A altura de um satélite geocêntrico, em relação à superfície da Terra, em órbita circular, é aproximadamente igual a
Dados: G = constante de gravitação universal; M = massa da Terra; R = raio da Terra = 6, 4.106m; (G M / 4 π2)1/3 = 2,2.104ms-2/3; (24 horas)2/3 = 2,0.103 s2/3
![]()
14-(UNICAMP-SP) Em 1665, Isaac Newton enunciou a Lei da Gravitação Universal, e dela pode-se

obter a aceleração gravitacional a uma distância d de um corpo de massa M , dada por g=G.M/d2 sendo G = 6,7.10-11Nm2 /kg2 a constante de gravitação universal. Sabendo-se o valor de G, o raio da Terra, e a aceleração da gravidade na superfície da Terra, foi possível encontrar a massa da Terra, MT = 6,0.1024 kg.
A aceleração gravitacional sobre um determinado satélite orbitando a Terra é igual a g = 0,25m/s2.
A distância aproximada do satélite ao centro da Terra é de
a) 1,7.103 km.
b) 4,0.104 km.
c) 7,0.103 km.
d) 3,8.105 km.
15-(UEMG-MG)

A figura a seguir representa dois satélites artificiais em órbita, em torno da Terra.
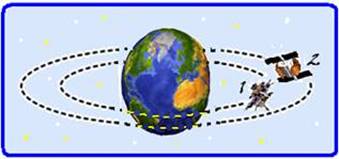
Baseando-se nas leis de Kepler, e diante da representação mostrada, É CORRETO afirmar que
A) os satélites 1 e 2 possuem a mesma velocidade.
B) o satélite 2 percorre uma distância maior que o satélite 1, num mesmo intervalo de tempo.
C) o satélite 2 leva mais tempo que o satélite 1 para dar uma volta completa em torno da Terra.
D) os satélites 1 e 2 dão uma volta completa em torno da Terra no mesmo intervalo de tempo.
16-(UNICAMP-SP)

Em 2011 o Atlantis realizou a última missão dos ônibus espaciais, levando quatro astronautas à Estação Espacial Internacional.

a) A Estação Espacial Internacional gira em torno da Terra numa órbita aproximadamente circular de raio R = 6800 km e
completa 16 voltas por dia. Qual é a velocidade escalar média da Estação Espacial Internacional?
b) Próximo da reentrada na atmosfera, na viagem de volta, o ônibus espacial tem velocidade de cerca

de 8000 m/s, e sua massa é de aproximadamente 90 toneladas. Qual é a sua energia cinética?
17-(FGV-SP)

Curiosamente, no sistema solar, os planetas mais afastados do Sol são os que têm maior quantidade de satélites naturais, principalmente os de maior massa, como Júpiter e Saturno, cada um com mais de 60 satélites naturais.

Considere 2 satélites A e B de Júpiter. O satélite A dista R do centro de Júpiter e o satélite B dista 4R do mesmo centro. Se A demora n dias terrestres para completar uma volta em torno de Júpiter, o número de dias terrestres em que B completa uma volta em torno do mesmo planeta é
![]()
