Leis de Kepler da Gravitação Universal – Resolução
Resolução comentada dos exercícios de vestibulares sobre
leis de Kepler da Gravitação Universal
01- C (vide teoria)
O2- A (vide teoria)
03- (01 + 02 +08)=11(vide teoria)
04- E (vide teoria)
05- Regra de três — 1 volta – 12 meses — ¼ volta – T — T=3 meses R- D
06- a) De 1o de Abril a 30 de Maio = 60dias — regra de três — 365 dias – 6,98.1022 — 60 dias — A — A=69,8.6.1022/365 — A»1,14.1022m2
b) Segunda lei de Kepler (lei das áreas)
07- TOP=TMN, pela segunda lei de Kepler, e VMN(afélio)<VOP(periélio), como conseqüência dessa lei.
R- B
08- Energia cinética=movimento=velocidade R- E
09- TT2/RT3= TP2/RP3 — (1)2 ano/(1)3 ua = TP2/(2,5)3ua — Tp2=(2,5)3 — TP=2,5.√(25/10) — TP » 4 anos terrestres
b) Como quanto maior a distância do planeta ao Sol, maior é o ano desse planeta (terceira lei de Kepler, lei dos períodos), portanto será mais curto.
10- T12/R13=T22/R23 — (24)2/(42)3.109=T2/(105)3.106 — T=3√2 — R- A
11- 322/13=322.82/R3 — R3=(23)2 — R=4u
12- C (vide teoria)
13- Observe a figura abaixo — M: massa do Sol — m: massa do planeta — r: raio da órbita — 
: velocidade orbital do planeta;
: força gravitacional; — 
: força resultante centrípeta — 3ª lei de Kepler afirma que: “o quadrado do período de translação
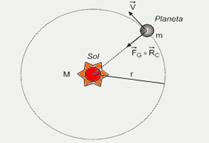
(T) do planeta é diretamente proporcional ao cubo do raio de sua órbita” — T2 = k r3 — como o movimento é circular uniforme, a força gravitacional comporta-se como resultante centrípeta — FG=RC — GMm/r2=mV2/r (I) — V=ΔS/Δt=2πr/T — V2=4π2r2/T2 (II) — (II) em (I) — 4π2r2/T2=GM/r — r3/T2=GM/4π2 — T2=4π2r3/GM — observe que G,M e π são todos constantes constituindo uma só constante k — T2=kr3
14- As três afirmações são, nessa mesma ordem, a 1ª, 2ª e 3ª Leis de Kepler — R- E
15- I. Correta — um ano luz corresponde à distância percorrida pela luz em ano, no vácuo.
II. Correta.
III. Errada — m/s2 é uma das unidades de aceleração
R- D
16- Da 3ª lei de Kepler: o quadrado do período de translação (ano do planeta) é diretamente proporcional ao cubo do raio médio da órbita — T2 = k r3, podemos concluir que quanto mais distante do Sol orbitar o planeta, mais longo é seu ano — portanto, os chamados planetas internos, Mercúrio e Vênus, têm anos mais curtos do que o ano terrestre — R- D
17- 1. Falsa — quando a Terra vai do afélio para o periélio, aumenta o módulo da velocidade, e quando vai do periélio para o afélio, diminui o módulo da velocidade.
2. Verdadeira — de acordo com o princípio da ação-reação (3ª lei de Newton), ação e reação têm sempre a mesma intensidade.
R- C
18- Observe pela figura abaixo que, se o efeito da gravitação deixasse de existir, o planeta sairia pela tangente entrando em
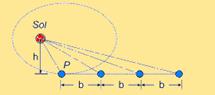
movimento retilíneo uniforme, percorrendo sempre a mesma distância b em temos iguais, portanto varrendo a mesma área — A = b/2 — R- A
19- 1. Falsa. O campo magnético da agulha existe, porém, para que essa agulha sofra alguma deflexão, ela tem que sofrer influência de outro campo magnético.
2. Verdadeira. Se a agulha da bússola não sofre deflexão, é porque ela não está em presença de algum campo magnético, sendo, portanto, nulo o campo magnético na Lua.
R- B
20- O ano terrestre é o período de translação da Terra em torno do Sol (tempo que a Terra demora para efetuar uma volta completa ao redor do Sol) — se a nova órbita fica mais perto do Sol — r’ < r — usando a 3ª lei de Kepler — (T’/T)2=(r’/r)2 — observe nessa expressão que se r’< r — T’< T — o que torna o ano terrestre mais curto — o período aproximado do ciclo lunar é T = 27 dias — o novo período é T’ = 80 dias — usando novamente a 3ª lei de Kepler — (r’/r)3=(80/27)2 — r’≈
— r’≈2r — R- B
21- R- C — veja teoria
22-01. Correta.
02. Falsa — Galileu Galilei afirmou que Sol ocupava o centro do Universo com os planetas girando ao seu redor.
04- Falsa — Kepler conclui que as órbitas eram elípticas baseado nas observações e anotações de Tycho Brahe.
08- Falsa — é exatamente o contrário (veja fisicaevestibular-lei das áreas de Kepler).
16. Falsa — para velocidades próximas às da luz são válidas as leis de Einstein.
32- Verdadeira.
Corretas: 01 e 32 — Soma=33.
23- Pode ser resolvida pela segunda lei de Kepler (lei das áreas) de enunciado: “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las”
Então:
A1/∆t1 ~A2/∆t2=constante=K
Essa constante K depende do planeta e recebe o nome de velocidade areolar
Observe na expressão acima que quando A1=A2 — ∆t1= ∆t1, ou seja, para o arco maior 34, ser percorrido no mesmo intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol – periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio — como a força resultante sobre o cometa é o produto de sua massa pela sua aceleração e como a aceleração é maior no afélio (ponto P), a força resultante sobre ele no afélio (ponto P) deverá ser maior — ou ainda, a intensidade da força resultante sobre o cometa corresponde à força de atração gravitacional entre ele e o Sol, fornecida por FR=G.M.m/r2 — veja que, como G,M e m são constantes, a intensidade da força resultante sobre o cometa é inversamente proporcional à distância r e, como no afélio r é menor, nele a força resultante terá maior intensidade.
24- Copérnico propôs o modelo heliocêntrico que afirmava que a Terra girava ao redor do Sol, contrariando os dogmas da igreja católica — Copérnico nada afirmou sobre as formas das órbitas, mais tarde declaradas como elípticas pela Primeira Lei de Kepler — Einstein propôs a teoria da relatividade modificando o conceito espaço tempo e revolucionando a física — suas
Idéias foram questionadas na Alemanha devido ao fato de ser judeu — enviou uma carta ao presidente dos Estados Unidos na qual contestava a utilização de suas teorias para fins bélicos — R- D
25- a) Verdadeira — Segunda lei de Kepler (lei das áreas) — “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las”
Essa constante K depende do planeta e recebe o nome de velocidade areolar — observe na expressão acima que quando A1 = A2
— ∆t1 = ∆t2, ou seja, para o arco maior 34, ser percorrido no mesmo intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol – periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio), — portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.
b) Falsa — as órbitas são elípticas com o Sol ocupando um dos focos da elipse — primeira lei de Kepler.
c) Falsa — O verão não ocorre quando a Terra está no periélio e nem o inverno quando ela está no afélio — as estações ocorrem devido ao fato de áreas da Terra, devido à inclinação da mesma, receberem mais ou menos luz do Sol durante seu movimento de translação.
d) Falsa — veja justificativa a.
e) Falsa — são válidas para todo o Universo.
R- A
26- Substituindo os dados fornecidos na expressão da terceira lei de Kepler, também fornecida — (Tj/TT)2 = (RJ/RT)3 — (TJ/1)2 =(7,5.1011/1,5.1011)3 — TJ2 = 53=125 — TJ = √(125) — TJ=11,180 anos terrestres — R- C
Observação: Na realidade, a terceira lei de Kepler afirma que T2/R3=K’=constante — observe que a medida que R aumenta, T também aumenta, o que significa que quanto mais afastado o planeta estiver do Sol maior será seu ano (tempo que demora para dar um volta completa ao redor do Sol) — para dois planetas quaisquer como, por exemplo, Terra e Marte, vale a relação TT2/RT3=TM2/RM3 — ao efetuar um volta completa ao redor do Sol num período (ano) T um planeta percorre ∆S=2πR e sua velocidade orbital vale V=∆S/T — T=2πR/V, que substituída em T2/R3=K’ fornece 4π2R2/VR3=K’ — V=4π2/K’R — V=constante/R — V é inversamente proporcional a R ou seja, quanto mais afastado o satélite ou planeta estiver, menor será sua velocidade orbital.
27-
Aplicando a lei dos cossenos — d2 = d12 + d22 – 2.d1.d2.cos120o — d=√(RJ2 + RT2 –
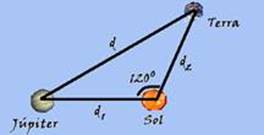
2.Rj.RT.cos120o) — d=√(RJ2 + RT2 -2.RJ.RT.(-1/2) — d=√(RJ2 + RT2 + Rj.RT) — R- D