Aceleração da Gravidade – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Aceleração da Gravidade

01- Nos pólos (vide teoria) R-C

02- g=GM/R²  —  R_p=1,5R_T  —  M_p=M_T=M  —  g_p/g_T=GM/1,5R_T²xR_T²/GM  —  g_p=4g_T/9 

03- g=GM/R²  —  g e R são inversamente proporcionais  —  R_equador>R_médio>R_pólo  —  g_equadoer<g_médio<g_pólo  R- B

04- A massa é a mesma na Terra e na Lua e vale m=90kg  —  Lua  —  P=mg  —  150=90g  —  g»1,6m/s²

05- V=V_o + a.t  —  0=4 + g.2,5  —  g=-1,6m/s²  —  ∆S=S_o + V_o.t + g.t²/2  —  ∆S=4.2,5 – 1,6.2,5²/2  —∆S=h=5m  R-B

06- Na superfície g_o=GM/R²  —  na altura h=2R + r=3R  —  g_h=GM/(3R)²  —  g_h=GM/9R²  —  g_h=g_o/9

07- a) g=GM/R²  —  g=7.10^-11.7.10²²/(2.10⁶)²  —  g=1,2m/s²

b) P=mg  —  P=80.1,2  —  P=96N

08- C (vide teoria)

09- Imponderabilidade  R-E

10- E (vide teoria)

11- I) Falsa – a força que age sobre ele é a força resultante centrípeta que é igual à força gravitacional (peso)

II) Correta – vide I         

III) Falsa – exerce sim, pelo princípio da ação e reação        

IV) Verdadeira – V=√GM/R – V e R são inversamente proporcionais

12- Aplicando a equação de Torricelli  —  V²=V_o² + 2gh  —  V_o=0 (partem do repouso)  —  V²=2gh  —  energia cinética em cada caso  —  E_cT=mV_T²/2 =m.2g_T.h/2 —  E_cL=mV_L²/2 =m.2g_L.h/2  —  como a gravidade na superfície da Lua é menor do que na superfície da Terra, a energia cinética ao atingir o solo lunar é menor do que ao atingir o solo terrestre  —  na queda livre  — 

h = gt²/2  —  t=√2h/g  —  observe que o tempo de queda é inversamente proporcional a √g  —  como g_L < g_T, o tempo de queda na Lua é menor do que na Terra  —  R- A

13–

R- B

14- Aceleração da gravidade  —  g_T=GM_T/R_T²  —  g_T=G80M_L/(4R_L)²  —  g_L=G.M_L/R_L²  —  g_T/g_L=G80M_L/16R_L² x R_L²/GM_L  — g_T= 5g_L  —  período  —  T_T=2π√l/g_T=2π√l/√5.√g  —  T_L=2π√l/√g  —  T_T/T_L=1/√5  —  R- A

15- Do enunciado  —  M_G=3M_T  —  r_G=0,2r_T  —  T=37 dias  —  V_G=0,5V_T  —  r (raio da órbita)  —  R (raio do planeta)

I. Falsa  —  g_G=GM_G/R_G²=G3M_T/R_G²  —  g_T=GM_T/R_T²  —  g_G=g­_T  —  3GM_T/R_G²=GM_T/R_T²  —  3/R_G²=1/R_T²  —  R_G=√3.R_T  — 

R_G=1,73R_T (deve ser 1,73 vezes maior).

II. Verdadeira  —  velocidade orbital  —  V=√GM/r  —  V²=GM/r  —  r_G – distância de Gleese 581g à estrela  —  r_T  —  distância da Terra ao Sol  —  velocidade orbital de Gleese 581g  —  V_G²=GM_estrela/r_G  —  (0,5V_T)²=GM_estrela/0,2r_T  —  0,25V_T²=GM_estrela/0,2r_T  —  V_T²=GM_estrela/0,05r_T (I)  — velocidade orbital da Terra  —  V_T²=GM_Sol/r_T (II)  —  igualando (I) com (II)  —  GM_estrela/0,05r_T=GM_Sol/r_T  —  M_estrela=0,05M_Sol=5%M_Sol (menos que a metade).

(III) Correta  —  uma face é sempre clara e a outra sempre escura.

(IV) Falsa  —  W=V/r  —  W_G=V_G/r_G=0,5V_T/0,2r_T  —  W_G=2,5V_T/r_T  —  W_G=2,5W_T (é maior)

 R- C

16- Em todo movimento circular existe uma aceleração de direção radial, sentido para o centro da circunferência e de intensidade  —  ac=V2/R  —  pelo enunciado ac=g  —  g=V2/R  —  W=V/R  —  V=W.R  —  g=(W.R)2/R  —  g=W2.R  —  W2=g/R  —  W=√(g/R)  —  R- A. 

17- A aceleração centrípeta do satélite no ponto P que é a própria aceleração da gravidade criada pela Terra nesse ponto  é dada

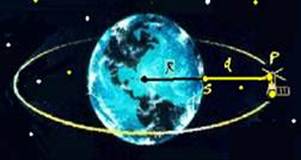
por g_P=G.M/(R + d)²  —  do enunciado g_P=g_S/10=10/10  —  g_P=1m/s²  —  1=6,7.10^-11.6,0.10²⁴/(6,4.10⁶ + d)²  —  (6,4.10⁶ + d)²=40,2.10¹³  —  6,4.10⁶ + d = √(402.10¹²)  —  6,4.10⁶ + d = 20.10⁶  —  d=1,36.10⁷m  —R- C

 

Voltar para os exercícios