Estática de um Ponto Material – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Estática de um Ponto Material

 

01- Sobre o homem atuam três forças, seu peso (vertical e para baixo) e as duas forças de tração aplicadas pelo teto através dos fios, agindo sobre suas mãos  —  R- A

02- A parede da direita aplica em B, sobre a esfera 2 uma força horizontal e para a esquerda, analogamente,  parede da esquerda aplica em A, sobre a esfera 2 uma força horizontal e para a direita e a esfera 1 comprime-a em A  —  R- A

03-

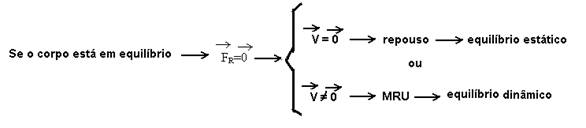
R- C

04- Quando elas tiverem mesma direção e mesmo sentido  —  valor máximo da terceira força que deve anula-las Fmáx=20 + 5=25N  —  quando elas tiverem mesma direção e sentidos opostos  —  valor mínimo da terceira que deve anula-las Fmín=20 – 5=15N  —  R- D

05- Observe atentamente a figura abaixo onde todas as forças foram colocadas

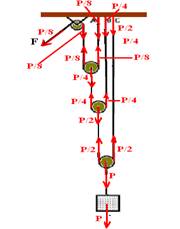
R- A

06- Colocando as forças que agem nos imãs  —  Fm – força magnética que deve ser de atração, caso contrário não haveria equilíbrio  —  peso P  —  T1 – força de tração no fio de cima  —  T=2 – força de tração no fio de baixo

R- C

07- (1)  —  2T1=P  —  T1=P/2  —  (2) 2T2sen60o=P  —  T2=P/2sen60o  —  T2=0,58P  —  (3) 2T3sen30o=P  —  T3=P/2sen30o  —  T3=P  —  R- B

08- m2/m1=3/2  —  m2=3/2m1  —  Fat=μN=μP2=μm2g  —  Fat=3/2μm1g  —  P1=m1g  —  colocando as forces:

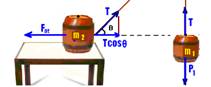
O bloco m1 está em equilíbrio  —  T=P1  —  T=m1g  —  o bloco m1 também está em equilíbrio  —  equilíbrio horizontal  —  Fat=Tcosθ  — 3/2μm1g =Tcos30o  —  3/2μm1g=m1g.√3/2  —  μ=√3/3

09- Colocando as forças

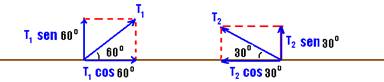
Equilíbrio na horizontal  —  T1cos60o=T2cos30o  —  T1.1/2=T2.√3/2  —  T1=√3.T2  —  equilíbrio na vertical  —  T1sen60o + T2sen30o=P  —  T1.√3/2 + T2.1/2=6.10  —  (√3.T2.√3)/2 + T2/2=60  —  3T2 + T2=120  —  T2=30N  —  T1=√3.T2  —  T1=√3.30  —  T1=30√3N

10- colocando as forças

 

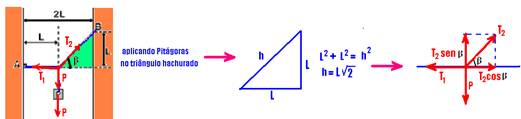
senβ=L/(L√2)  —  senβ=√2/2  —  cosβ= L/(L√2)  —  cosβ=√2/2  —  equilíbrio vertical  —  P=(√2/2)T2  —  T2=P√2  —  R- D

11- Observe a figura abaixo:

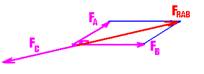
FRAB=FA2  FB2=(160)2 + (120)2  —  FRAB=200N=FC­  —  R- E

12– a) Observe na figura abaixo que 2T=P=mg=60.10  —  T=600/2  —  T=300N

b) Prolongando as duas cordas obtemos os dois triângulos da figura abaixo

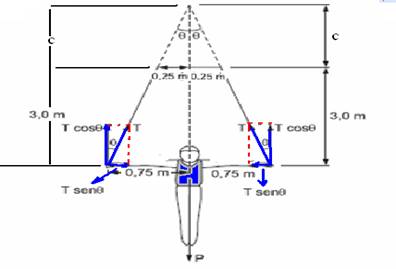
Pela semelhança entre os triângulos de alturas c e (3 + c)  —  0,25/c=0,75/(3 + c)  —  c=1,5m  —  equilíbrio na vertical  —  2Tcosθ=P  —  Tcosθ=300   —  T=300/cosθ (I)  —  na horizontal, a componente horizontal de T é  —  Tx=Tsenθ  —  T=Tx/senθ (II)  —  igualando (I) com (II)  —  300/cosθ=Tx/senθ  —  senθ/cosθ=Tx/300  —  tgθ=Tx/300  —  0,75/4,5=Tx/300  —  Tx=50N

13- Para que as placas fiquem em equilíbrio estático, resultante das força que agem sobre elas devem ter componentes na horizontal e na vertical para que possam se anular  —  observe que a única alternativa que não tem componentes que possam se anular na horizontal é a V  —  R- E

14- Para movê-lo, a força de tração deve valer T=500N, conforme a figura abaixo:

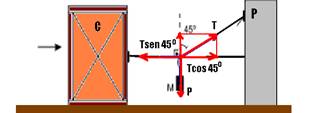
Equilíbrio na horizontal  —  Tcos45o=500  —  T√2/2=500  —  T=500√2N  —  equilíbrio na vertical  —  Tsen45o= P  —  500√2.(√2/2)=P  —  P=500N  —  para movê-lo é necessário um peso de 500N, ou seja, 500/150=3,3 blocos  —  R- D

15- a) Somente quando α=β

b) Colocando as forças:

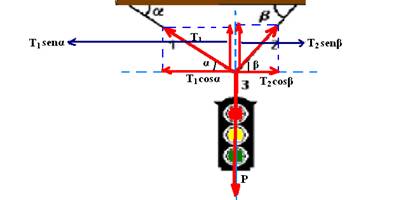
Equilíbrio na horizontal  —  T1cosα=T2cosβ  —  T1√3/2=T2.1/2  —  T2=√3.T1  —  equilíbrio na vertical  —  T3=P=100N  –—  100=T1sen30o + T2sen60o  —  100=T1.1/2 + (√3T1).√3/2  —  100=T1/2 + 3T1/2  —  T1=50N  —  T2=√350  —  T2=50√3N

16- Ângulo de 60o  —  F1=2Tcos60o=2T1/2=T  —  ângulo de 45o  —  F2=2Tcos45o=2T√2/2=√2T  —  F1=√2F2  —  R- B

17- a)

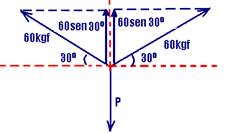
equilíbrio na vertical  —  2.60.sen30o=P  —  2.60.1/2=P  —  P=60kgf

b) analogamente  —  2.130.sen30o=P  —  P=130kgf  —  130/30=4,33  —  4 crianças

18- Colocando as forças:

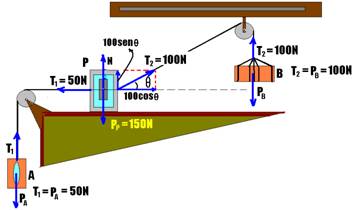
Equilíbrio vertical no bloco P  —  150=N + 100senθ  —  150=N + 100.0,87  —  N=63N  —  R- E

19-

Equilíbrio na vertical  —  Fcos60o=P + 8,8.103  —  F.1/2=8,8.103  + 200 —  F=(8.800 + 200).2  —  F=18.000  —  F=18.103N

20- Observe a figura abaixo:

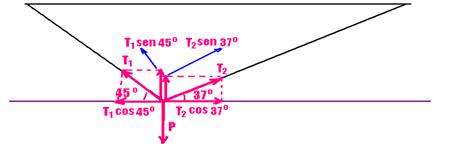
Equilíbrio na horizontal  —  T1cos45o=T2cos370  —  T1.0,7=T2.0,8  —  T1=8T2/7  —  equilíbrio na vertical  —  T1sen45o + T2sen37o=P  —  T1.0,7 + T2.0,6=280  —  (8T2/7).0,7 + 0,6T2=280  —  0,8T2 + 0,6T2=280  —  T2=280/1,4  —  T2=200N  —  R- C

21- Se os tratores e o barco se movem em trajetória retilínea com velocidade constante eles estão em equilíbrio dinâmico e a resultante das forças que agem sobre eles é nula  —  F1=F2=F  — 

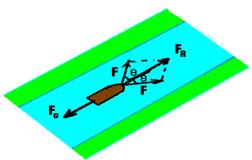
FR=2Fsenθ=2F.0,8  —  FR=1,6F  —  FR=Fc  —1,6F=1,92.104  —  F=1,20.104N  —  R- A

22- Equilíbrio na vertical —  Tsen45o=P  —  T√2/2=55  —  T=55√2N  —equilíbrio na horizontal  —  

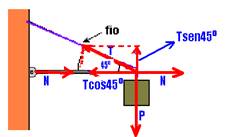
N=Tcos45o  —N=55√2.√2/2  —  N=55N  

23- Se você pendurar um quadro na parede por meio de dois fios, quanto menor for o ângulo formado com o teto, ou o suporte, maior será a força de tração (tensão) no fio.Exemplo:

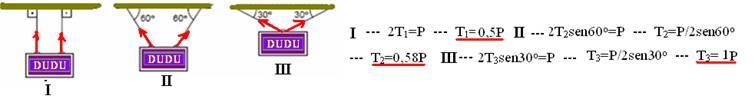
R-  T1 > T2 > T3

24- R- A  (veja resolução do exercício anterior)

25- Observe a figura abaixo:

senθ=0,2/5  —  senθ=0,04  —  Ty=Tsenθ=0,04T   —  2Ty=P  —  2.0,04T=20  —  T=2540N  —  R- D 

26- senβ=30/50  —  senβ=0,6  —  P=2Tsenβ  —  36=2T.0,6  —  T=36/1,2  —  T=30N  —  R- E

27- Nas figuras abaixo estão colocadas as forças que  agem sobre a esfera  —  como a esfera está em equilíbrio, a resultante das

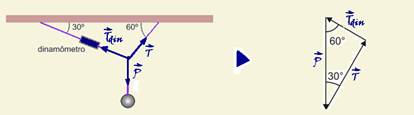
forças é nula  —  sen30o=Tdin/P  —  1/2=10/P  —  P=20N  —  R- D

28- a) Observe o diagrama abaixo que mostra as forças atuantes no terceiro elo:

b) Dados  —   m = 200 g = 0,2 kg  —   g = 10 m/s2  —  P = m g = 0,2(10)  —  P = 2 N  — F43 = 2 P = 4 N  —  F23 = 3 P = 6 N

29- Observe nas figuras abaixo onde cada força de tração é decomposta na vertical (TV=Tsen60o) e na horizontal (TH=Tcos60o)  — 

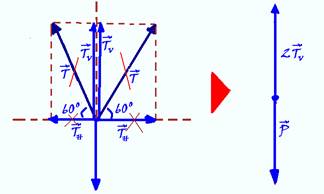
Como o sistema está em equilíbrio, as componentes horizontais se anulam e na vertical você terá  —  2T­V=P  —  2Tsen60o=P  —  2T.√3/2=50  —  T=50/√3N  —  R- C

30- m = 10 kg  —   xA = 5 cm  —   sen θ = 0,6  —   cos θ = 0,8  —  g=10m/s2  —  observe as figuras a seguir onde o corpo está em equilíbrio nas duas situações e a resultante das forças deve ser nula em

 cada caso  —  figura A  —  FA=P  —  kxA=mg  —k.5=10.10  —  k=20N/cm  —  figura B  —   e  se anulam  —  FB=Pt  —  kxB=mgsenθ  —  20.xB=10.10.0,6  —  xB=3cm  — 

R- D 

31- Dado: P1 = 500 N.

Como é uma situação de equilíbrio, a resultante em cada um dos nós R e S é nula  —  aplicando, então, a regra da poligonal em

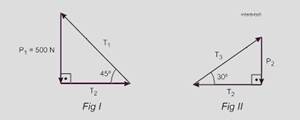
cada um dos nós  —  figura I  —  sen45o=P1T1  —  √2/2=500/T1  —  T1=500√2N  —  tg45o=P1/T2  —  1=500/T2  —  T2=500N  — 

Figura II  —  cos300=T2/T3  —  √3/2=500/T3  —  T3=1000/√3N  —  tg30o=P2/T2  —  √3/3=P2/500  —  P2=500/√3N  —  R- A

 

32- Observe na figura 1 abaixo no triângulo hachurado a determinação do ângulo θ entre a horizontal e a direção da força normal,  de contato entre a quina do degrau e a roda  —  senθ=(R/2)/R  —  senθ=1/2  —  θ=30o  —  n a figura 2, todas as forças que agem sobre a roda, normal  de contato entre o piso e a roda, peso ,  e , foram colocadas no centro (eixo) da roda  —    na figura 3,  foi decomposta em sua componente horizontal N1.cos30o=N1√3/2 e vertical N1sen30o=N1/2  —  à medida que  for aumentando de intensidade para erguer a roda, a intensidade da força normal  vai diminuindo, até que, quando a roda perder contato com o piso (N=0), ela começa a subir (figura 4)  — no instante em que ela perde contato com o piso ela está em equilíbrio e a resultante das forças que agem sobre ela é nula  —  equilíbrio na horizontal  —  F=N1√3/2  —  equilíbrio na vertical  —  N1/2=P  —  N1=2P  —   F=N1√3/2=2P.√3/2  —  F=mg√3  —  R-C.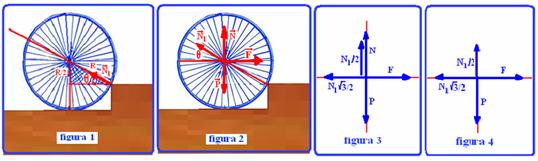

 

 33- Para calcular a intensidade da força resultante que age sobre a partícula cósmica você pode decompor as forças nas direções norte e leste  —  observe na sequência abaixo que a intensidade da

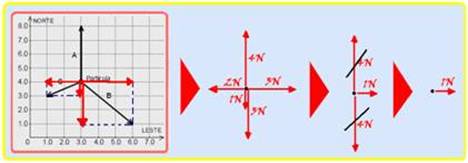
força resultante é de 1N no sentido leste.

Como a velocidade inicial da partícula tem intensidade Vo=1200m/s do norte para o sul e a força resultante sobre ela tem intensidade 1N do oeste para leste, o movimento da partícula tem as características de composição de dois movimentos, um no sentido leste e outro no sentido sul (veja figura)  —  no sentido leste, a projeção da velocidade inicial é nula VoL=0 e ela se desloca sob ação de uma força resultante de valor FR=1N e com aceleração  —  FR=m.a  —  1=2.10-3.a  —  a= 500m/s2  —  sua velocidade nessa direção após t=1s terá intensidade  —  VL=VoL + aL.t=0 + 500.1  —  VL=500m/s  —  no sentido sul ela será lançada para baixo com VoS=1200m/s, acelerando com aceleração da gravidade g=10m/s2  —  após t=1s, sua velocidade nessa direção será  —  VS=VoS + g.t=1200 + 10.1=1210m/s  —

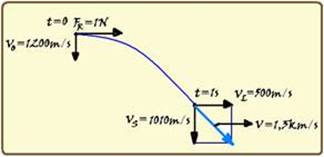
 observe na figura que essas duas velocidades são perpendiculares e, aplicando Pitágoras você obterá V2 = VL2 + VS2=(500)2 + (1210)2  —  V=√(1714100)  —  V=1309m/s=1,3km/s  —  R- A.

34- Pelo princípio da inércia, se as forças deixarem de atura, a força resultante sobre ela será nula e, após esse innstante, por inércia, ela seguirá em MRU com velocidade constante de 1,3km/s  —  observe na resolução do exercício anterior (08) que, antes de 1s a trajetória era parabólica  —  R- D.

 

35- Colocando as forças  —  bloco 1  —  Fat=μN=μP1=μm1g  —  bloco2  —  P2=m2g  —  P3=m3g  — 

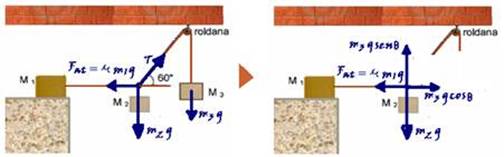
decompondo a tração T  —Thorizontal=mgcosθ  —  Tvertical=mgsenθ  —  equilíbrio na horizontal  —  μm1g=m3gcos60o  —   μm1g=m3g.(1/2)  —  μ=m3/2m1  —

R- A

36- a) As forças que agem sobre o conjunto imã-grampo são  —   – força peso, vertical e para baixo, aplicada sobre o conjunto

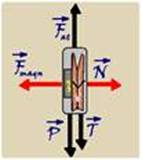
pela Terra  —   – força de tração no fio, vertical e para baixo, aplicada sobre o conjunto pela massa M pendurada  —  – força de atrito, trocada entre o conjunto  e a parede da geladeira, vertical e para cima, contrária ao movimento ou à sua tendência  —   –  força magnética, horizontal e que atrai o conjunto para a esquerda, é de atração magnética entre o imã e a parede da geladeira  —   – força normal, horizontal e para a direita, reação da parede da geladeira sobre o conjunto.

b) Se o conjunto não deve cair a força resultante sobre ele tanto na vertical como na horizontal deve ser nula  —  equilíbrio na vertical  —  Fat=P + T  —  P=mog  —  T=Mg  —  Fat=μeN  —  μeN = mog + Mg (I)  —  equilíbrio na horizontal  —  FM=N (II)  —  (II0 em (I)  —  μeFM = mog + Mg  —  Mg = μeFM – mog  —  M= (μeFM – mog)/g ou M= μeFM/g – mo —  para esse valor de M o conjunto está na iminência de cair  —  para qualquer valor de M menor que esse, o conjunto não cai.

37- Cálculo de d na figura 1 —  triângulo retângulo – Pitágoras  —  d2 = 302 + 402  —  d=50cm  —  cálculo de h1  —  triângulo amarelo

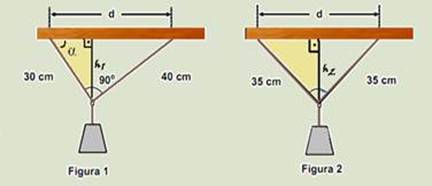
da figura 1  —  senα=h1/30  —  triângulo inteiro  —  senα=40/d  —  h1/30=40/50  —  h1=24cm  —  aplicando Pitágoras no triângulo amarelo da figura 2  —  352 = (d/2)2 + h22  —  1225 = 252 + h2  —  h=√(600)  —  h≈24,5cm  —  o trabalho da força peso é fornecido pela expressão  —  Wpeso=m.g.∆h=10.10.(0,245 – 0,24)  —  Wpeso=0,5J  —  R- C

 

Voltar para os exercícios