Estática de um corpo extenso – Resolução
Resolução comentada das questões de vestibulares sobre
Estática de um corpo extenso –Centro de Massa – Tipos de Equilíbrio
01- Localizando o centro de massa de cada bloco e colocando a origem do referencial no centro de massa do bloco 1:
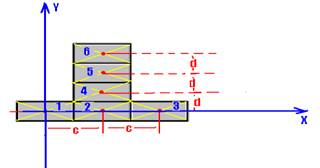
XCM=(mX1 + mX2 + mX3 + mX4 + mX5 + mX6)/6m = (m.0 + m.c + m.2c + m.c + m.c + m.c)/6m — XCM=6mc/6m –XCM=c — YCM=(m.0 + m.0 + m.0 + m.d + m.2d + m.3d)/6m — YCM=6md/6m — YCM=d — localizando CM.
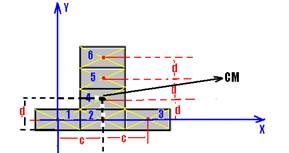
R- D
02- Localizando o centro de massa de cada placa e suas respectivas coordenadas — circular –
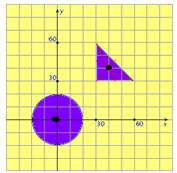
C(0,0) — triangular T (40,40) — XCG=(mXC + mXT)/(m + m)=(m.0 + m.40)/2m — XCG=20cm — YCG=(mYC + mYT)/2m=(m.40 + m.40)/2m — YCM=20cm — XCM + YCM=20 + 20 = 40 cm
03- bandeja – b mb=0,4kg — prato -A – – mA=0,5kg — copo – B – mB=0,1kg — garrafa – C – mC=1,0kg —XCG=(mb.Xb + mA.XA + mBXB + mCXC)/(mb + mA + mB + mC)= (0,4..0 + 0,5.(-2). + 0,1.(-10) + 1.(+4+)/(0,4 + 0,5 + 0,1 + 1,0)=2/2 — XCG=1cm — YCG=(mb.Yb + mA.YA + mBYB + mCYC)/(mb + mA + mB + mC)=(0,4.0 + 0,5.(-5) + 0,1.5 + 1.4)/2 — YCM=2/2 — YCM=1cm — R- E
04- Colocando a origem do sistema de coordenadas no centro de massa da esfera 1 em O1.
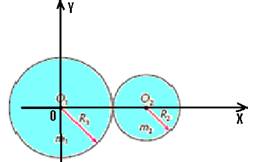
R1=2R2 — m2=2m1 — XCM=(m1X1 + m2X2)/(m1 + m2)=(m1.0 + 2m1.(R1 + 2R1)/3m1 — XCM=6m1R1/3m1 — XCM=2R1 — YCM=(m1Y1 + m2Y2)/(m1 + m2)=(m1.0 + m2.0)/3m1 — YCM=0 — CM(2R1,0) — R- C
05- Colocando o centro de massa em cada bloco e os valores de suas respectivas abscissas e
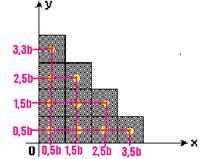
ordenadas — XCM=(4m.0,5b + 3m.1,5b + 2m.2,5b + m.3,5b)/10m=15mb/10m — XCM=1,5b — YCM=(4m.0,5b + 3m.1,5b + 2m.2,5b + m.3,5b)/10m=15mb/10m — YCM=1,5b — CM (1,5b;1,5b)
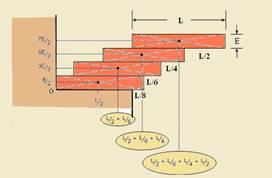
06- O centro de massa dos três blocos da esquerda está em B e o dos quatro blocos da direita está em E. Assim, o centro de massa do sistema está sobre a reta que une B e E — R- B
07-

R- D
08- Ao se levantar ela perde contato com a cadeira, pois a reta vertical que passa pelo seu centro de
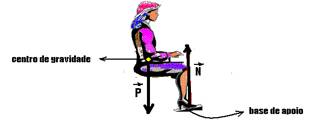
gravidade (onde está o peso) não coincide com a base de apoio (onde está a normal) que estão em seus pés. Assim, ela retorna à cadeira, sem levantar.
09- Colocando os centros de gravidade em cada bloco e analisando os blocos A e B (figura abaixo)
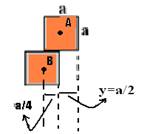
— para que o bloco A esteja na iminência de cair, y deve valer y=a/2 — para que A e B estejam na
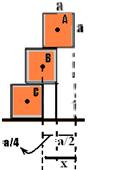
iminência de cair, o bloco C deve ser colocado como na figura acima — x=a/4 + a/2 — x=(2a + 4a)/8 — x=3a/4
10- Para que ele não tombe, a reta vertical que passa pelo centro de gravidade deve passar pela
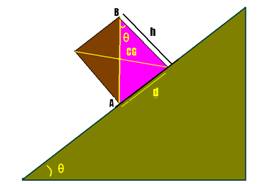
extremidade A da base de apoio — no triângulo hachurado — tgθ=d/h — h=d/tgθ — h=d.cotgθ — R- D
11- R- E
12- Como o centro de gravidade CG está sempre no ponto médio e à medida que o cigarro vai queimando ele se desloca para a esquerda, quando o cigarro estiver na iminência de cair, você terá a
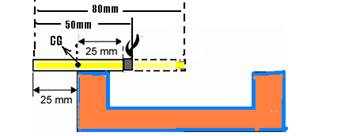
situação da figura abaixo, onde você deve observar que o cigarro queimou d=80 – 50=30mm com velocidade de 5mm/min — V=d/t — 5=30/t — t=6 min
13- Corpo apoiado — I – CG está na junção – indiferente — II – CG está acima da junção – instável — III – CG está abaixo da junção – estável — R- E
14- Corpo suspenso — I – CG abaixo do ponto de suspensão – estável — II – CG acima do ponto de suspensão – instável — III – CG coincide com o ponto de suspensão – indiferente
15- Condição para que o bloco não deslize (iminência de escorregar)
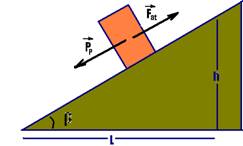
— PP=Fat — psenβ=μPcosβ — μ=tgβ=h/L (I)
Condição para que o bloco não tombe — a reta vertical que passa pelo centro de gravidade deve passar pela extremidade A da base.
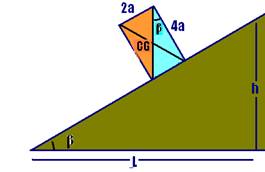
tgβ=2a/4ª — tgβ=1/2 (II) — igualando I com II — h/L=1/2 — R- d
16- Situação I — cargas de mesmo sinal se repelem — se você girar levemente a carga negativa de B para baixo a força de repulsão entre ela e a negativa de A diminui, mas a de repulsão entre as positivas de A e de B aumenta, fazendo com que a barra retorne à situação inicial – equilíbrio estável — situação II — cargas de sinais opostos se atraem — se você girar levemente a negativa de B para cima a força de atração entre ela e a negativa de A aumenta,enquanto que a força de atração entre a positiva de A e a negativa de B diminui, fazendo com que a barra B continue girando — equilíbrio instável — R- E
17-A figura mostra as abscissas x1; x2; x3 e x4 e as ordenadas y1; y2; y3 e y4 dos quatro corpos — abscissa X do centro de massa –
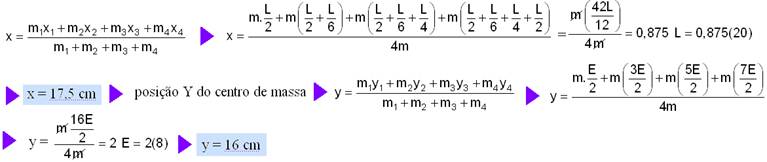
18- O torque a(momento) realizado pelo fio corresponde ao momento da força de tração de
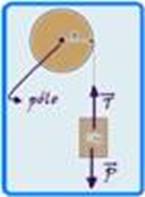
intensidade — FR= P – T=m.a —P – T=m.a — m.g – T = m.a — 1.10 – T = 1.3 — T=7N — o torque da força de tração no fio é fornecido por — M= F.d — M =T.R=7.0,2 — M=1,4N.m — R- B
19- O peso dos dois recipientes é o mesmo — se os dois tivessem apenas água até a borda a balança estaria em equilíbrio — mas, com a madeira flutuando no recipiente B e com água até a borda, a balança continuará em equilíbrio, pois quando você colocou a madeira ela deslocou um volume de líquido que possui o mesmo peso que a parte imersa da madeira “Princípio de Arquimedes”.
20- I. Falsa — observe pelo gráfico fornecido que a medida que o ângulo φ vai diminuindo a força exercida pelos músculos sobre a coluna vai aumentando e a coluna fica muito solicitada diminuindo a possibilidade de levantar pesos maiores.
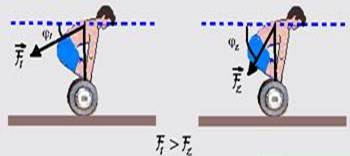
II. Correta — a medida que o ângulo φ aumenta a força exercida pelos músculos sobre a coluna diminui e a coluna fica menos solicitada o que possibilita ao atleta elevar pesos maiores.
III. Correta — a medida que o ângulo φ aumenta a força exercida pelos músculos sobre a coluna diminui e a coluna fica menos solicitada, diminuindo a tensão na musculatura eretora.
R- E
