Estática de um corpo extenso – Máquinas Simples – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Estática de um corpo extenso – Máquinas Simples

 

01- A única força que não precisa ser decomposta no sentido de girar a barra no sentido horário é F₂  —  R- A 

02- O portão tende a girar no sentido horário  —  R- A

03- F_A=F_B=F  —  M_FA=+F.a  —  M_FB=+F.a  —  M_FC=0  — M_R=+2Fa  —  gira no sentido horário  —  R- A

04- a) O momento resultante é a soma algébrica do momento de cada força em relação ao ponto O  —  M₁=+F₁.d₁=+1,0.10⁴.100  —  M₁=10,0 .10⁵N.m  —  M₂=-F₂.d₂=-2,0.10⁴.80  —  M₂=-16,0.10⁵N.m  —  M_R=10,0.10⁵ – 16,0.10⁵  —  M_R=-6,0.10⁵N.m  —  M_R=6,0.10⁵N.m e tende a girar no sentido anti-horário

b) F_R=3.10⁴N  —  Δt=1min=60s  —  I=F.Δt=3.10⁴.60  — I=1,8.10⁶N.s

05- Para desatarraxar  —  M₁=F.d=400.15  —  M₁=6.000N.cm  —  com a extensão  —  M₂=M₁=F₂.d₂  —  6.000=F₂.75  —  F₂=6.000/75  — F₂=80N

06- Jovem 

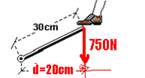
M_j=F.d=750.20  —  M_j=15.000N.cm  —  namorada  —  M_n=510.30  —  M_n=15.300N.cm  —  sim, consegue

07- M_h=+F_h.d=80.10  —  M_h=800N.cm  —  M_m=-F_m.d=-5.200  —  M_m=1.000N.cm  —  ganha o menino  —  R- B

08- As forças que agem sobre o trampolim estão indicadas abaixo

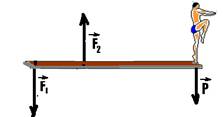
R- C

09- Para abrir a porta  —  M₁=F.d=20.0,4  —  M₁=8N.m  —  esse momento é o que o menino deve aplicar para abri a porta com força de 10N a uma distância d  —  M=F.d  —  8=10.d  —  d=0,8m

10- Fd=F’d/2  —  F’=2F  —  R- C

11- Observe que os momentos das forças F₂ e F₃ são nulos, pois a linha de ação dessas forças coincide com o eixo de

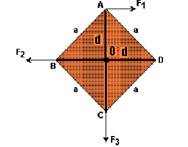
 rotação (pólo O), não fazendo, portanto a chapa girar. Quem a tende a girar é o momento de F₁ tal que M_F1=F.d e que deve ter o mesmo módulo que o momento de F₄ (M_F4=F₄.d)  —  M_F1=M_F4  —  Fd=F₄d  —  F₄=F  —  a força F, aplicada em D deve impedir a tendência de rotação provocada por F=1 e, assim, F em D deve ser vertical e para cima  —  R- D

12- (1) – Verdadeira  —  não existe atrito entre a escada e o chão, então ela escorrega não podendo ficar em equilíbrio.

(2) –  Falsa  —  decompondo as forças conforme figura abaixo:

(3) – Falsa  —  depende da direção e sentido de cada força

(4) – Verdadeira  —  quanto menor o ângulo com o teto (), maior será a força de tração nele.     

R- V F F V

13- R- C  —  veja figura abaixo

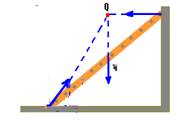
14-

a)

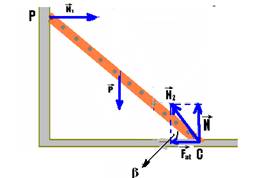
b) Sim, desde que ela não escorregue em C, onde deve ter atrito para manter o equilíbrio  —  a força normal  tem a mesma intensidade que o peso   —   N=P=mg=40.10  —  N=400N  —  tgβ=4/3  —  tgβ=N/Fat  —  4/3=400/Fat  —  Fat=1.200/4  —  Fat=300N

15- a)

b) Decompondo a força  que o chão troca com a barra

 

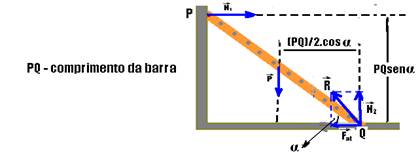
Equilíbrio na horizontal  —  N₁=F_at  —  equilíbrio na vertical  —  N₂=P  —  colocando o pólo em Q  —  a soma algébrica dos momento sé igual a zero  —  M_N1=N₁.PQsenα  —  M_P=P.(PQ)/2.cosα  —  M_Fat=M_N2=0  —  +F_at.PQ.senα – P.(PQ)/2.cosα=0  —  2.F_at.senα=P.cosα  —  tgα=P/2F_at  —  F_at=μP  —  tgα=P/2μP  —  tgα=1/2.0,25  —  tgα=2

16- Colocando as forças que atuam na régua e colocando o pólo em P  —  P_corpo=mg=9.10^-3.10  — 

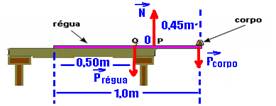
M_Prégua=- P_régua.d= – P_régua.0,05  —  M_N=0  —  M_Pcorpo= + P_corpo.d=+9,0.10^-2.0,45=4,05.10^-2N.m  —  a soma dos momentos deve ser nula  —  – 0,05.P_régua + 4,05.10^-2=0  —  P_régua=4,05.10^-2/5.10^-2=0,81N  —  m_régua=0,81/10=0,081kg=81g  — m_régua=81g

17- Para que a prancha esteja na iminência de tombar, a força de reação normal N₁, no primeiro apoio deve ser nula (N₁=0)  —   o cilindro deve estar a uma distância x do segundo apoio  —  a soma dos momentos de cada força deve ser nula  —

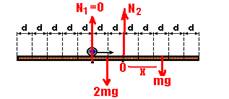
–  colocando o pólo O no ponto de aplicação de N₂ (segundo apoio) —  0.2d – 2mg.d + N_2.0 + mg.x=0  —  2mgd=mgx  —  x=2d  —  R- B

18- a) Observe a figura abaixo:

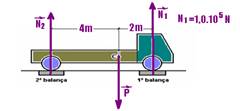
Colocando o pólo em N₂  —  a soma dos momentos em relação ao pólo deve ser nula  —  M_N2=0  —  M_P=+P.4  —  M_N1=-N₁.6  — M_N1=-6.10⁵N.m  —  +4P – 6.10⁵=0  —  P=6.10⁵/4  —  P=1,5.10⁵N

b) N₁ + N₂=1,5.105  —  1,0.10⁵ + N₂=1,5.1⁵5  —  N₂=0,5.10⁵  —  N₂=5,0.10⁴N

19- I – Correta  —  veja teoria  —  II – Correta  —  dentro da água o corpo E fica mais leve devido ao empuxo, vertical e para cima e fora da água ele tenderá a descer, fazendo a barra girar em torno de C no sentido horário  —  III – Falsa  —  veja II  —  R- D

20- a) colocando o pólo em C  —  -F.d + P.a=0  —  -F.0,04 + 20.0,3=0  —  F=150N

b) colocando o pólo em F  — -C.d + P.(a – d)=0  —  -C.0.04 + 20.(0,3 – 0,04)=0  — C=130N

21- Colocando o pólo em F_M  —  600.30 – F_P.120=0  —  F_P=150N  —  colocando o pólo em F_M  —  -600.90 + F_M.120=0  —  F_M=150N  —  R- C

22- A soma dos momentos de todas as forças em relação ao pólo 0 deve ser nula  —  -F.4 +23.20 + 100.35=0  —  F=990N

23- A distância máxima (x) que o homem pode se deslocar sobre o trilho a partir de P, ocorre quando o trilho estiver na

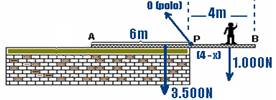
iminência de girar e, nessas condições N_A=0  —  com o pólo em P  —  + (3.500).1 – 1000.(4 – x)=0  —  x=0,5m  —  d=4 – x  —  d=3,5m

24- Observe o comprimento das hastes em relação ao ponto de apoio e verifique que o lado de comprimento 5cm deve equilibrar o dobro da massa que o lado de comprimento 10cm (figura abaixo)

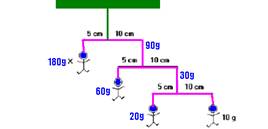
R- C

25- Colocando o pólo em N₁

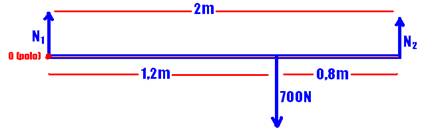
+700.1,2 – 2N2=0  —  N₂=420N  —  R- C

26- P=90.10³.10  —  P=9.10⁵N  —  polo em D  —  -9.10⁵.16 + 2N_T.20=0  —  N_T=36.10⁵N  —  M_T=36

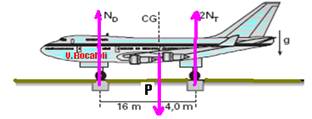
toneladas  — 90=36 + M_D  —  M_D=18 toneladas  —  R- C

27- Primeira situação  —  colocando o pólo em M  —  a soma dos momentos de cada força em relação ao pólo deve ser

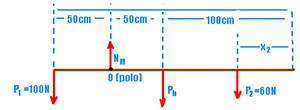
nula  —  – 100.50 + 50P_b + 60(150 – x₂)=0  —  -5.000 + 50P_b – 9.000 – 60x₂=0  —  5P_b– 6x₂= – 400 (I)

Segunda situação  —   colocando o pólo em M  —  a soma dos momentos de cada força em relação ao pólo deve ser

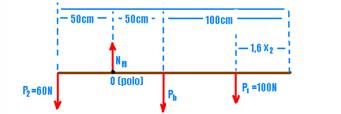
nula  —  -60.50 + 50P_b + 100(150 – 1,6x₂)=0  —  -3.000 + 50P_b + 15.000 – 160x₂=0  — 5P_b – 16x₂= -1.200 (II)  — 

resolvendo o sistema composto por I e II  —  x₂=80cm  —  P=16N  —  m=16/10  — m=1,6kg

28- Pólo em N

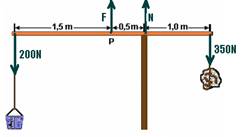
-200.2 + F.0,5 + 350.1=0  —  -400 + 0,5F + 350=0  —  F=100N  —  R- D

29- pólo no apoio  —  -25.140 – 30.100 – 50.60 + 40.60 + m.100 + 30.140=0  —  m=2.900/100  —  m=29kg  —  R- B

30- colocando as forças e o pólo na posição indicada e lembrando que no equilíbrio de translação  —  T=P=3.000N

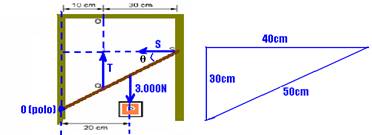
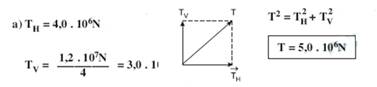
+T.10 -3.000.20 + S.30=0  —  3.000×10 – 60.000 + 30S=0  —  S=1.000N  —  T/S=3.000/1.000  —  T/S=3

31-

 

E=dvg=10^3..10^-3.10  —  E=10N  —  E.d_AB – F.d_BC=0  —  10.5 – F.1=0  —  F=50N  —  R- A

32- Observe a figura abaixo:

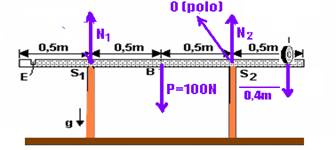
+100.0,5 – 0,4P=0  —  P=125N  —  m=125/10  —  m=12,5kg  —  a maior massa a partir dessa é 10kg  —  R- B

33-

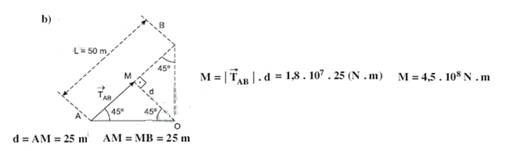
34- a) Interpotente  —  a força aplicada pelo operador  (potência) localiza-se entre o pólo e a força transmitida (resistência) .

b) Observe a figura  —   a soma dos momentos de cada força em relação ao pólo deve ser nula  —  -F_P.30 + 20.70 +

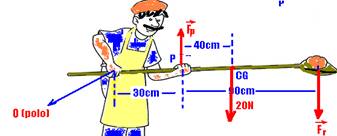
5.120=0  —  F_P=690/30  —  F_P=23N

c) η=F_r/F_P=5/23  —  η=22%

35- Observe a relação F₂/F₁=d₁/d₂  —  se d₁ > d₂ – F₂ > F₁  —  R- C

36- a) Pressão=força/área  —  P=F_c/S  —  1,3.10⁹=F_c/0,1.10^-6  — F_c=1,3.10⁹.10^-7  —  F_c=1,3.10²  —  F_c=130N

b) d_c=2.10^-2m  — F_c=130N  — a soma dos momentos das forças em relação ao eixo de rotação deve ser nula  —   -F_c.d_c + F_a.d_a=0  —  130.2.10^-2=F_a.10.10^-2  —  F_a=260/10  — F_c=26N

37- Interpotente  —  a força aplicada pelo operador  (potência) localiza-se entre o pólo e a força transmitida (resistência) .

b) -F_p.d₁+Mg.d₁ + mg(d₁ + d₂)=0  —  F_p=(Mg.d₁ + mg(d₁ + d₂))  —  F_p=Mg + (mg(d₁ + d₂))/d₁  —

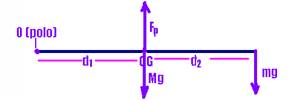
 F_p= 

38- 1- interpotente  —  2- interpotente  —  3- interpotente  —  4- interfixa  —  5- interpotente  —  6- interfixa  — 

7- interfixa  —   8- interpotente  —  9- inter-resistente

39- Observe a figura abaixo:

Havendo equilíbrio  —  -F_r.dr + F_r.d_p=0  —  F_r/F_p=d/a  —  como a>d  — F_p tem que ser maior que F_r  para que o equilíbrio seja mantido  —  R- B

40- Trata-se de uma alavanca interfixa  — supondo que a força exercida por Arquimedes seja seu próprio peso, por

 exemplo de massa 75kg  —  p=75g  —   -F_p.d_p + F_r.d_r=0  —  75g.d_p=6.10²⁴g.d_r  —  d_p/d_r=6.10²⁴/75  — 

d_p/d_r=8.10^-2.10²⁴  —  d_p/d_r=8.10²² (d_p deve ser 8.10²² vezes maior que d_r).

41- a) interpotente

b) F_p.d_p – F_r.d_r=0  —  1.200.2=F_r.8  —  F_r=300N

42- 4.OA – F.4OA=0  — F=1N  —  alavanca interpotente

43- a)  

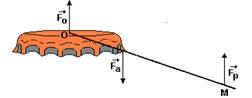
F_p = força exercida pela pessoa que opera o abridor  —  F_a = força de reação que a tampinha exerce no abridor na região da borda da tampinha  —  F_o = força de reação que a tampinha exerce no apoio

b) F_p.8,4 – F_a.1,4=0  —  F_p/F_a=0,17

 

44- a) Momento de uma força é a grandeza vetorial que mede o poder de uma força provocar rotação  —  depende da intensidade da força F e do módulo da distância d da linha de ação da força até o eixo de rotação, denominada braço da alavanca  —  expressão matemática  —  M_F=F.d.senα, onde α é o ângulo entre F e d.

Aplicações práticas:A chave de roda para se trocar um pneu, o martelo, o alicate, a maçaneta da porta e o próprio abrir e fechar da

porta.

b) Para arrastar objetos pesados torna-se menos dificultoso fazê-lo em etapas, apoiando uma extremidade e girando a outra, alternadamente.

Esse truque é muito usado pelos operários de empresas que fazem mudanças. Ao transportar móveis (geladeira, fogão, guarda-roupas etc.) em vez de levantar os objetos, um funcionário apoia uma das extremidades, enquanto outro dá um pequeno giro no móvel, aplicando força na outra extremidade. A seguir, invertem-se as operações. Prosseguindo essa alternância, o móvel vai avançando. 

45- Observe a figura abaixo  —  equilíbrio de translação  —  a resultante das forças na vertical deve

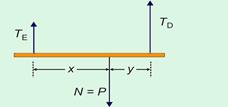
ser nula  —  T_E + T_D=P  — equilíbrio de rotação  —  a soma dos momentos de cada força deve ser nula  —  pólo em P  —  +T_E.(x) – T_D.(y)=0  — 

T_E.(x)=T_D.(y)  —  observe que, como x>y, T_E deve ser menor que T­_D  —  T_E<T_D  —  R- C

46- Como a alavanca está em equilíbrio de rotação, o somatório dos momentos horários é igual ao somatório dos momentos anti-horários  —  com o pólo (eixo de rotação) indicado na figura  —  Q.(x) = P.(y)  —  200x=600y  —  x=3y  —  R- C

47- Na situação 1  —  F=Q  —  Q/F=1  —  na situação 2  —  F.3=Q.1  —  Q/F=3  —  R- A

48- Observe na figura que, se o comprimento da barra for L, cada divisão corresponde a L/6  —  como a barra está em equilíbrio,

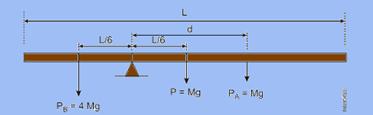
soma dos momentos horários é igual à soma dos momentos anti-horários  —  chamando de P_A o peso do corpo A, de P_B o peso do corpo B e de P o peso da barra, colocando-os conforme  a figura você terá matematicamente, com o pólo no ponto de apoio (cunha)  —  M.P_B=M.P + M_.P_A  —  P_B.(L/6) = P.((L/6) + P_A.d  —  4.M.g.L/6 = M.g.L/6 + M.g.d  —  d=3L/6 (à direita da cunha)  a  — R- C

49- Observe as forças colocadas na figura abaixo  —  como não há rotação, o somatório dos momentos em relação ao eixo de rotação é nulo  —  matematicamente  —  F.(8) = F’.(4)  —  2.(8) =4.F’  —  F’ = 4 N  —  R- A

50- Como é uma situação de equilíbrio de um corpo extenso, temos que considerar equilíbrio de translação (a resultante das forças deve ser nula) e equilíbrio de rotação (o momento resultante deve ser nulo). Analisando cada uma das opções:

a) Falsa. A resultante das forças na direção horizontal é não nula.

b) Falsa. A resultante das forças na direção vertical é não nula.

c) Correta.

d) Falsa. O momento resultante é não nulo, provocando rotação no sentido horário.  

R- C

51- Observe na figura abaixo as forças que agem na gangorra  —  a soma dos momentos das forças no sentido horário devem se

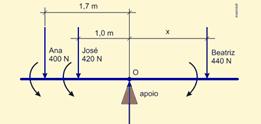
igualar com a soma dos momentos das forças no sentido anti-horário  —  440x=400×1,7 + 420×1  — 440x=1100  —  x=2,5m  —

R- D

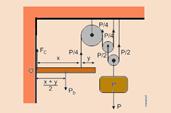
52- A figura a seguir mostra as forças atuantes nas polias, bem como as forças atuantes na barra, sendo P_b o peso da barra, aplicado

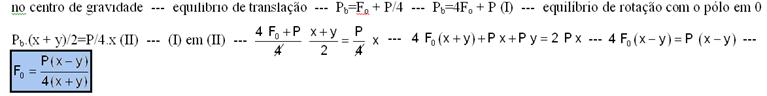
53- Na figura abaixo estão colocadas as forças que agem no prisma que está em equilíbrio  — 

colocando o pólo em O  — F.x=P.2  —  10.x=15.2  —  x=3m  —  R- C

54-

55- Observe na figura abaixo as forças que agem sobre o braço que está na horizontal  —  peso da

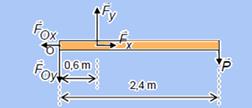
massa M  —  P=mg=430.10  — P=4300N  —  P=4,3kN  —  para que o braço esteja em equilíbrio, o somatório dos momentos (torque) nos sentidos horário e anti-horário deve ser nulo  — polo em O  —   F_y.0,6 – P.2,4=0  —  F_Y=17,2kN  — a força  é a soma vetorial de  com   — veja

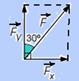
esquema  —  cos30^o=F_x/F  —  F_x= Fcos30^o  —  F=F_x/cos30^o=17,2kN/0,86  —  F=20kN

b) Pressão=força/área  —  P_r=4,5N/3.10^-2.0,2.10^-3=4,5/6.10^-6  —  P_r=7,5.10⁵N/m² (Pa)

56-

 

57- Observe a figura abaixo com o pólo P no eixo de rotação  —  cálculo do momento de cada força

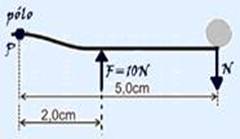
em relação ao pólo estabelecendo como positivo o sentido horário de rotação  —  M_10N = -10.2=-20N.m  —  M_N=+N.5  —  a somatória de todos os momentos deve ser nula para que haja equilíbrio de rotação  —  M_10N + M_N = 0  —  – 20 + 5N = 0  —  N=4N  —  R- D

58- No equilíbrio antes de colocar o recipiente  —  colocando as forças   —  equilíbrio de translação 

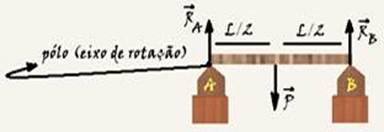
—  R_A + R_B=P (I)  — equilíbrio de rotação com o pólo em A  —  M_RA=R_A.d=R_A.0=0  —  M_P=+ p.L/2  —  M_RB= – R_B.L  —  a somados momentos de cada força é nula  —   +P.L/2 – R_B.L=0  —  R_B=P/2 (II)  —  R_A=R_B=P/2   —  após a inclusão do recipiente, quando o mesmo estiver totalmente cheio de líquido de peso P_líquido  —  equilíbrio de translação  —  R_A + R_B=P + P_líquido  —  equilíbrio de rotação  —  M_RA=0  —  M_Plíquido= –

P_líquido.x  —M_P= – P.L/2  —  M_RB=R_b.L  —  0 – P_líquido.x – P.L/2 + R_B.L=0  —  R_B=(P_líquido.x + P.L/2)/L  —  R_B=(2 P_líquido.x + P.L)/2L  — à medida que o líquido vai preenchendo o recipiente seu volume V’ e consequentemente seu peso (P_líquido) vão aumentando provocando um aumento de R_A e como o exercício pede, de R_B  —  observe também que a relação entre R_B e P_líquido e consequentemente V’ do líquido é uma função do primeiro grau, ou seja, o comportamento de R_B é linear  —  R- A

59- Primeira situação  —  equilíbrio de rotação  —  a soma dos momentos de cada força com o pólo

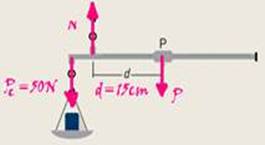
 em N (N=0) é nula  —  M_pc=-50x  —  M_N=0  —  M_P=+15P  —  -50x + 15P=0  —  x=15P/50  —  x=3P/10

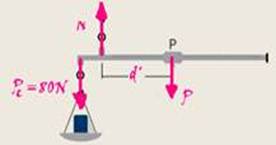
(constante)  —  segunda situação  —  P_c=80N  — d’=?  —  a soma dos momentos com o pólo em N (N=0) deve ser nula  —  -80x + Pd’= 0  —  -80.(3P/10) = Pd’  —  d’ = 24 cm  —  R- C

60- Equilíbrio de translação  —  cálculo da intensidade da força de tração  —  T=30 + 6=36N  — 

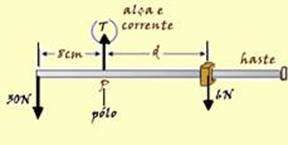
equilíbrio de rotação  com o pólo (eixo de rotação em T)  —  a doma dos momentos de cada força em relação ao pólo deve ser nula  —  M_30N= – 30.8 = – 240N.cm  —  M_T=T.d=T.0=0  —  M_6N= + 6.d  —  ΣM=0  —  -240 + 0 + 6d = 0  —  d= 240/6  —  d= 40cm  —  R- E

61- Seja F a força aplicada pelo motorista no pedal  —  pelo enunciado a alavanca tem a capacidade 

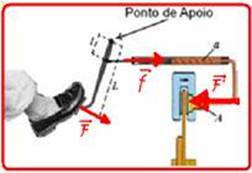
de ampliação da força aplicada por um fator igual à razão direta de seus braços, que é de 40/10=4 vezes  —  f=4F  —  a prensa hidráulica amplia a força f na razão direta de suas áreas, ou seja, de 8 vezes  —  F’=8f  —  F’=8.4F  —  F’=32F  —  R- A.

62-  –01. Correta  —  a forçamínima necessária, aplicada no braço de alavanca para manter suspensas as 5 barras de ferro, de peso P=5.mg=5.5.10=250N ocorre quando o sistema está em equilíbrio  —   como as duas polias são fixas elas transmitem integralmente a intensidade da tração T=250N através do fio até a extremidade direita do disco  —  equilíbrio de rotação com o pólo (eixo de rotação) no centro do disco  —  momento de cada força  —  M_F=+F.d=F.1  —

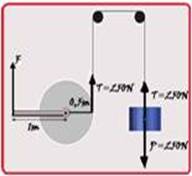
M_F= F  —  momento de T=250N  —  M_T= – T.d= – 250.0,5= – 125N.m  —  a soma dos momentos de cada  força deve ser nulo  —  F – 125=0  —  F=125N.

02. Correta  —  a velocidade de qualquer ponto do fio (2m/s) é a mesma que de qualquer ponto da periferia do disco de raio r=0,5m que também é de v=2m/s  —  velocidade angular do disco que é constante para qualquer ponto do mesmo e vale  —  W=v/r=2/0,5=4rad/s  —  o braço de alavanca gira em torno de uma circunferência de raio R=1m e sua velocidade v vale  —  W=v/R  —  4=v/1  —  v=4m/s.

04. Falsa  —  cálculo da tração T no fio com F=250N  —  M_250N=+250.1=250N.m  —  M_T= – T.0,5  —  250 – 0,5T=0

 —  T=500N  —  essa força é totalmente transmitida pelas polias fixas até o peso de P=250N  —  F_R=m.a  —  T – P=m.a  —  500 – 250=25.a  —  a=250/25  —  a=10m/s².

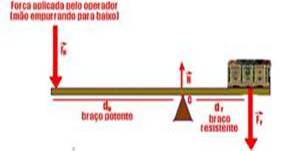
08. Correta  —  Alavanca interfixa – o apoio está entre a força potente e a força resistente

16. Falsa  —  Se F for inclinada em relação à d, você pode calcular o momento da força decompondo-a em suas componentes horizontal x e vertical y.

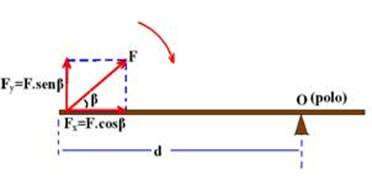
Fx não produz rotação e seu momento é nulo  —  quem produz rotação é apenas Fy=Fsenβ  —  M=Fy.d  —  M=Fsenβ.d.

Corretas: 01, 02 e 08  —  Soma=11.

63- Colocando as forças que agem sobre a trave  —  peso  da trave, vertical e para baixo e de intensidade  —  P=m.g=4,6.10  —  P=46N  —  força de tração aplicada pelo cabo, sustentando-a  —  decompondo a força em suas componentes horizontal e vertical  —  horizontal – T_h=T.sen60^o=T.√3/2  —  vertical – T_v=T.cos60^o=T.1/2=T/2  — 

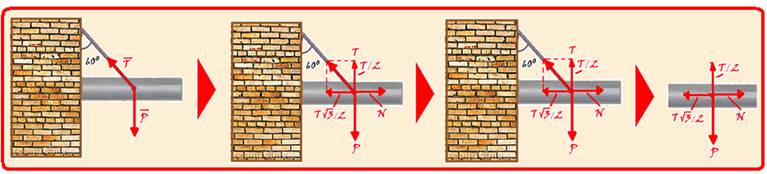
Observe a seqüência da figura acima  —  N é a intensidade da força horizontal que a parede aplica na trave  —  equilíbrio na horizontal  —  N=T.√3/2  —  equilíbrio na vertical  —  T/2=P  —  T/2=46  —  T=92N  —  se fosse pedida a intensidade da força que a trave troca com a parede você teria  —  N=92.√3/2=46√3N.

64-  Observe na figura abaixo  —  equilíbrio de translação (não sobe nem desce)  —  T₁ + T₂= P_pi +

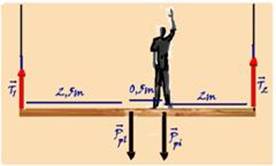
P_pl (I)  — equilíbrio de rotação (não gira)  —  colocando o pólo (eixo de rotação) em  e calculando o momento de cada força em relação ao pólo  —  M_T1=T₁.0=0  —  M_pl=+P_pl.d=600.2,5=1500N.m  —  M_pi=+P_pi.d=700.3=2100N.m  —  M_T2= – T₂.d= – 5T₂  —  a soma dos momentos de cada força deve ser nula  —  0 + 1500 + 2100 – 5T₂ = 0  —  T₂=720N   —  substituindo T₂=720N em (I)  —  T₁ + 720 = 1300  —  T₁=580N  —  R- A.

65- Observe a figura abaixo onde estão localizadas todas as forças que agem sobre a barra  — 

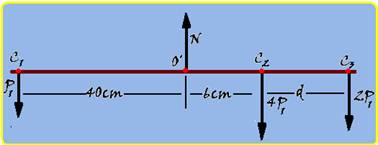
cálculo do momento de cada força com o pólo em O’  —  M_P1= – P₁.40= – 40P₁  —  M_N=N.0=0  —  M_4P1= + 4P₁.6= + 24P₁  —  M_2P1= + 2P₁.(d + 6)  —  a condição de equilíbrio de rotação é que a soma dos momentos de todas as forças for nula  —  – 40P₁ + 0 + 24P₁ +

2P₁.(d + 6) = 0  —  – 16P₁ = – 2d – 12  —  d=2cm  —  a distância pedida entre os pontos O’ e C₃ vale  —  d’ = 6 + 2= 8cm  —  R- C.

 

Voltar para os exercícios