Trabalho de diversos tipos de forças – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Trabalho de diversos tipos de forças

01- a) Colocando todas as forças que agem sobre o carrinho

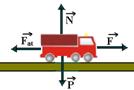
Cálculo da intensidade da força de atrito — F_at=m.N=m.P=m.m.g — F_at=0,2.10.10 — F_at=20N

Se o carrinho está com velocidade constante, a força resultante sobre ele é nula e F=F_at — F=20N

Trabalho de cada força:

W_F=F.d.cosα — W_F=20.5.cos0^o — W_F=100.(1) — W_F=100J (positivo, motor)

W_Fat=F_at.d.cos α — W_Fat=20.5.cos 180^o — W_Fat=100.(-1) — W_Fat= -100J (negativo, resistente)

W_N=W_P=P.d.cos α α =P.d.cos90^o=P.d.0=0 — W_N=W_P=0(perpendiculares ao deslocamento)

O trabalho da força resultante é nulo, pois F_R=0.

b) F_at=20N — a=3m/s² — F=m.a — F=10.3 — F=30N

Trabalho de cada força:

W_F=F.d.cos α — W_F=30.5.cos0^o — W_F=150.(1) — W_F=150J (positivo, motor)

W_Fat=F_at.d.cos α — W_Fat=20.5.cos 180^o — W_Fat=100.(-1) — W_Fat= -100J (negativo, resistente)

W_N=W_P=P.d.cos α =P.d.cos90^o=P.d.0=0 — W_N=W_P=0 (perpendiculares ao deslocamento)

Trabalho da força resultante — W_FR=150 – 100 + 0 + 0 — W_FR=50J ou W_FR=F_R.d.cosa=(30 – 20).5.cos0^o — W_FR=50.(1) — W_FR=50J

02- O trabalho realizado pela força resultante centrípeta é sempre nulo, pois ela é sempre perpendicular à velocidade (que

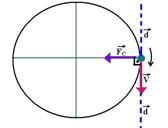
é sempre tangente em cada ponto da circunferência) e consequentemente ao deslocamento . R- C

03- W=F.d.cos α — W=30.10.1/2 — W=150J R- C

04- W_F=F.d.cos0^o — W_F=100.2.(1) — W_F=200J e o trabalho da força de atrito é negativo (a=180^o).

R- D

05- I- O trabalho da força de atrito não é nulo, é negativo – incorreta II- É nulo sim (a=90^o) – correta III- Não é nula, é igual ao F_at, pois está com velocidade constante e F_R=0 – incorreta R- B

06- Como ele não está sendo impulsionado, puxado ou empurrado, a força resultante sobre ele é a própria força de atrito.

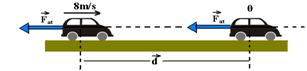
F_R=F_at=m.a — V²=V_O² + 2.a.d — 0²=8² – 2.a.d — a.d= – 32 — F_at=m.a — W_Fat=F_at.d.cos0^o=m.a.d.(1) — W_Fat=1.(-32).1

W_Fat=-32J R- D

07- F_at=m,N=m.P=0,2.2.10 — F_at=4N — F_R=F – F_at=20 – 4 — F_R=16N — W_FR=F_R.d.cos0^o=16.5.(1) — W_FR=80J

08- Força F₁ — W_F1=F_1..d.cosθ — W_F1=0,4.2,5.cosθ — W_F1=cosθ=k — Força F_{2 —}W_F2=F₂.d.cos2θ — W_F2=0,4.2,5.cos2θ — W_F2=cos2θ — cos2θ =cos²θ – sen²θ — cos2θ=k² – (1 – cos²θ) — cos2θ = k² – 1 + k² — cos2q = 2k² – 1 — W_F2=cos2q=2k² – 1 R-D

09- R- D (veja teoria)

10- F_at=mN — W_Fat=F_at.d.cos180^o — W_Fat=-mNd R- B

11- a) Distância percorrida DS — V=DS/Dt — 2=DS/2.400 — DS=4.800m essa seria a distâcia que ele percorreria se estivesse andando numa estrada reta, plana e horizontal.

O deslocamento que é uma grandeza vetorial é nulo em relação a um referencial (qualquer ponto) fixo no solo.

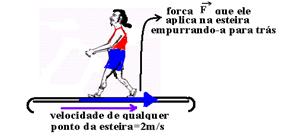
Consumo de calorias em joules — 1 cal – 4J — 300.000cal – xJ — x=4X300.000 — x=1,2.10⁶J — esse consumo de calorias é o próprio trabalho — W=F.DS.cos0^o — 1,2.10⁶=F.4.400.(1) — F=250N

12- Observe nas figuras abaixo que podemos decompor em e , sendo que quem realmente realiza trabalho é F_X=Fcosα,

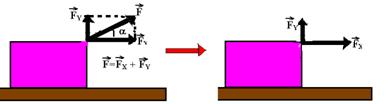
pois é a parcela de que efetivamente influi no deslocamento, tendo a direção e o sentido dele. Já a parcela que é perpendicular ao deslocamento não realiza trabalho, pois não influi no deslocamento.

13- Decompondo a força em e em — F_X=Fcosθ — F_Y=Fsenθ — equilíbrio na vertical — F + N = P — N=P – F_Y

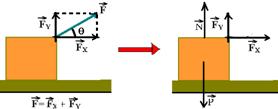
N = P – Fsenθ — e W_N=0 (θ=90^o) R- C

14- W=b.h/2 — W=1.10/2 — W=5J R- C 15- W=b.h/2 — W=x’.F’/2 — R- A

16-1- W=b.h/2=1.10^-2.15/2 — W=7,5.10^-2J verdadeira 2- F é constante e vale F=15N — F=ma — 15=1,5.a — a=10m/s²

Verdadeira 3- correta, se F=0 ele está em equilíbrio dinâmico (MRU) 4- W=1.10^-2.15/2 + 1.10^-2.15 + 2.10^-2.15/2 –

2.10^-2.12/2 — W=25,5.10^-2J Falsa — R- E

17– W=1.2/2 + 1.2 + 1.2/2 – 2.2/2 + 0 — W=2J

18- W=(12 + 4).10/2 + 12.5 — W=140J R-C

19- R- B (veja teoria)

20- W=m.g.h=70.10.2 — W=1.400J — ordem de grandeza — 1,4.10³ J — 1,4 está abaixo de 5 e se transforma em 1 —

W=1.10³ J R- C

21- a) peso do pilão manual — P=m.g=5.10=50N — W=P.h=50.0,6 — W=30J

b) peso do monjolo — P=m.g=30.10=300N — trabalho em uma queda — W=P.h=300.2 — W=600J

Considerando esse intervalo de tempo como 1s — manual- W=15J — monjolo – W=150J

Regra de três — 15J – 1 pessoa — 150J – n pessoas — n=10 pessoas

22- R- D (veja teoria)

23- O trabalho realizado (energia transferida) para elevar o mesmo balde a uma mesma altura com velocidade constante é o mesmo para Oscarito e Ankito, mas a força mínima exercida por Oscarito é menor, já que o deslocamento é maior (no caso, a polia móvel dobra o deslocamento e reduz a força à metade) — R- D

24- a) densidade do produto=massa do produto/volume do produto — d=1.000/(1.312,5 – 62,5) — d=0,8g/cm³

b) massa total de cada caixa – m=10 + 1.000 + 100=1.110g=1,11kg — peso de cada caixa – P=m.g=1,11.10 — P=11,1N

W=P.h — W=11,1.1,5 — W=16,65J

25- Trabalho do peso

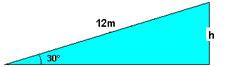
sen30^o=h/12 — 1/2=h/12 — h=6m — W_P=P.h=m.g.h=4.10^3..10.6 — W_P=240kJ

Trabalho da resultante — ∆S=d=V_o.t + a.t²/2 — 12=0.4 + a.16/2 — a=1,5m/s² — F_R=m.a=4.10³.1,5 —

F_R=6.10³N — W_FR=F_R.d.cos0^o=6.10³.12.(1) — W_FR=72kJ

26-01- Correta – a polia da direita (móvel) divide a força aplicada pela metade

02- Correta – como a velocidade é constante o corpo está em equilíbrio — fig. I — F=P — fig. 2 — F=Psen30^o=P/2

04- Correta – O trabalho da força peso independe da trajetória

08- Falsa – vide 04

Soma das corretas 07

27- De A para B — W_AB= -m.g.h=- 70.10.0,3 — W_AB= – 2.10 J — De B para C — W_BC=+m.g.h=+70.10.0,5 — W_BC= 350 J

W_total= – 2.10 + 3.50 — W_total= 1.40 J ou W_total= 1,4.10² J

ou W_AC=m.g.(h_BC – h_AB)=70.10.(0,5 – 0,3) — W_AC=1,4.10²J R- D

28- O trabalho realizado é numericamente igual à área — W=b.h/2=2.100/2 — W=100 J R- B

29- a) 8cm

b) A- F_e=k.X=20.0 — F_eA=0 — F_eB=20.0,08 — Fe_B=1,6N — F_eC=20.0,16 — F_eC=3,2N

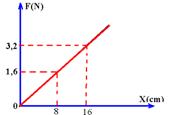
c) Como a força é variável — W_Fe=área do trapézio=(B + b).h/2=(3,2 + 1,6).(8.10^-2)/2 — W_Fe= – 0,192 J (negativo, forçado, F_e é contrário ao deslocamento)

W_F tem o mesmo valor, mas é positivo (a favor do deslocamento) — W_F=0,192 J.

30- V_o=7,2/3,6=2m/s — V=0 — DS=X=1m — Torricelli — V²=V_o² + 2.(-a).X — 0 = 4 +2.a — a=2m/s² — F_R=F_e=m.a — F_e=7,0.10⁴.2 — F_e=14.10⁴N — F_e=k.x — 14.10⁴=k.1 — k=14.10⁴N/m — W_Fe=k.X²/2=14.10⁴.1²/2 — W_Fe=7.10⁴J

31– Sobre o peixe agem duas forças — força de tração (que o pescador aplica para erguer o peixe, vertical e para cima) e o peso do peixe (vertical e para baixo) — como o deslocamento é para cima e o peso do peixe é para baixo, eles possuem sentidos contrários e o trabalho da força peso é resistente (contrário ao deslocamento) — R- A

32- a) O trabalho da força de atrito é dado por — W = F_at.d.cos180° — W = m.N.d.(-1) — W = – 0,60.3.2.10^-2 — W = – 3,6.10^-2 J

b) Pela leitura do gráfico dado temos que na tensão de 20 kV = 2.104 V tem-se uma pressão de 2.10⁸ N/m² — pressão =força/área

Força = pressão.área — Força = 2.10⁸.0,25.10^-6 — F= 50 N

33– (01) Correta — entre 0 e 4s — a=(V – V_o)/(t – t_o)=(45 – 0)/(4 – 0) — a_I=11,25km/s² — entre 7s e 9s — a=(V – V_o)/(t – t_o)=(0 – 45)/(9 – 7) — a_II=22,5km/s² — como a massa é a mesma (mesmo carro) e F_R=ma — F_RI=m.11,25 — F_RII=m.22,5 —

F_RII=2F_RI.

(02) Correta — no gráfico v ´ t a distância percorrida é obtida pela “área” entre a linha do gráfico e o eixo do tempo — área do trapézio — ΔS=(B + b).h/2=(9 + 3)/2.(45/3,6) — ΔS=75m.
(04) Errada — o trabalho total (entenda-se: trabalho da resultante) é igual à variação da energia cinética — como a velocidade final é igual à inicial, ambas nulas, o trabalho total é nulo.

(08) Errada — no gráfico, a “área” do triângulo de 0 a 4 s é o dobro da “área” do triângulo de 7 a 9 s — portanto, a distância percorrida de 0 a 4 s é o dobro da distância percorrida de 7 a 9 s.

(16) Correta — D = v Dt — 75=(45/3,6).Δt — Dt = 6s.

R- (01+ 02 + 16)= 19

34- Dados — F = 30 N — DS = 800 m — o trabalho (W) de uma força constante é dado pela expressão — W_F=F.d.cosα — sendo a força paralela ao deslocamento — a = 0°, cos a = 1 — W_F=30.(800) = 24.000 J = 24 kJ — R- D

35- Dados — m = 1.140 ton = 1,14 ´ 10⁶ kg — h = 710 m — g = 10 m/s² — W_F=m g h = (1,14.10⁶) (10) (710) = 8,094.10⁹ J = 8.094.000.10³ J — W_F=8.094.000 kJ — R- E

36- Dados — F = 5 N — d = 2 m — a = 15° — o enunciado nos permite construir a figura abaixo:

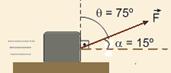
O trabalho de uma força é dado pelo trabalho de sua componente paralela ao deslocamento — T = F d cos a.

Porém, a e q são complementares — sen q = cos a — T = F d cos a = F d sen q — substituindo os valores dados —

T = 5.2.sen 75° — assim, q = 75°. — R- D

37- Dados — m₁ = 6 kg — m₂ = 1,5 kg — g = 10 m/s² — DS = 30 m — a = 60° — se a força é a necessária para levantar o corpo de massa m₂ com velocidade constante, então a intensidade dessa força é — F = P₂ = m₂ g = 15 N — trabalho realizado (W) para arrastar a mochila — W = F.DS.cos 60° = (15).(30).(0,5) — W = 225 J — R- B

38- O trabalho de força constante é calculado pela expressão — T = F d cos a — ela mostra que o trabalho (T) de força constante é diretamente proporcional ao deslocamento (d) — portanto, o gráfico T = f (d) é uma reta que passa pela origem — para os valores fornecidos — T = 4 (1) cos 60° = 4 (0,5) — T = 2 J — R- D

R- D

39- Analisemos cada uma das afirmações:

(I) Errada — W=F_R.d.cosα — se α=90^o — cos90^o=0 — W=0

(II) Errada — A 3ª lei de Newton afirma também que essas forças agem em corpos diferentes, portanto não se equilibram.

(III) Correta — É exatamente o que afirma o teorema da energia cinética: “o trabalho da resultante das forças que agem num corpo é igual à variação de sua energia cinética.” Portanto, se o trabalho é nulo, a energia cinética se mantém constante.

R- C

40- Dados — E = 94.684.781 MWh @ 9,5 ´ 10⁷ MWh = 9,5 ´ 10¹³ Wh — L = 0,45 ´ 10⁸ J/kg — transformando essa quantidade de energia em joules — E = 9,5 ´ 10¹³ Wh = (9,5 ´ 10¹³ W) ´(3,6 ´ 10³ s) = 3,4 ´ 10¹⁷ J — para o petróleo — E = m L — m =E/L=3,4×10¹⁷/0,45×10⁸ = 7,5 ´ 10⁹ kg = 7,5 ´ 10⁶ toneladas — m = 7,5 milhões de toneladas — R- D

41- O enunciado exige menor impacto ambiental. Já que a incidência solar na região é alta, a melhor forma para obtenção de energia é a fotovoltaica — R- D

42- Reservatório de energia — bateria e meio ambiente;

Transformador de energia — bateria e lâmpada;

Modo de transferência de energia — realizando trabalho elétrico sobre os elétrons-livres no interior do fio condutor

R- B

43- A tabela mostra a energia gasta em cada uma das atividades, dentro do tempo especificado em cada uma das proposições, destacando aquela que mais se aproxima do gasto de 304 quilocalorias.

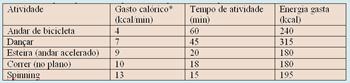
R- A

44- A parcela de F₁ que influi no deslocamento horizontal vale F₁’=F₁cos (90^o – 30^o) — F₁’=10.1/2=5N — para que o trabalho seja fornecido pela área, no eixo vertical a força deve ser a força resultante, cujos valores são fornecidos no gráfico abaixo —

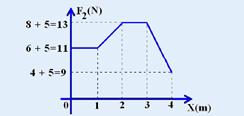
O trabalho total realizado pela força resultante é numericamente igual à soma das áreas — W=(1.11) + ((13 + 11).1/2 + ((1.13) + (13 + 9).1/2 — W_FR=47J — R- B

45-O trabalho da força resultante com ela atuando na mesma direção e sentido do deslocamento é numericamente igual à área entre a reta representativa e o eixo do deslocamento — W=área do triângulo=b.h/2=26.12/2 — W=156J — R- D

46-O trabalho realizado pela força peso da pessoa ao subir as escadas independe da trajetória e é, numericamente igual à variação

de sua energia potencial gravitacional — W=∆E_p=m.g.∆h=80.10.450 — W=360 000J=360kJ — são ingeridas 4 porções e o rendimento de cada uma é 25% (1/4), logo, a energia química de uma porção é convertida em trabalho — W=360kJ — R- E

47- Considerando o nível da jusante (parte mais baixa da água) nulo, o da montante (parte mais elevada da água) será

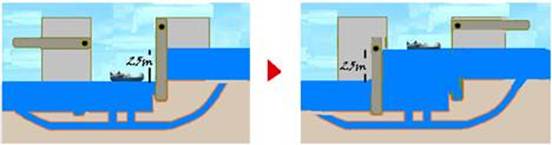
de 25m — ∆E_pg=m.g.∆h=1,2.10⁴.10.(25 – 0) — ∆E_pg=300.10⁴J=3,0.10⁶J — R- D

Trabalho de diversos tipos de forças – Resolução

Voltar para os exercícios