Tipos de Forças – Resolução
Resolução comentada dos exercícios de vestibulares sobre Tipos de Forças
01– A
02- Colocando todas as forças que agem em cada bloco.
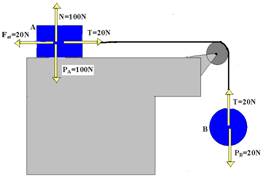
Como o bloco B está em equilíbrio — PB=T=20N — o fio ideal transmite a tração de 20N até o bloco A, puxando-o para a direita. Como o bloco A também está em equilíbrio, na vertical temos, N=PA=100N e na horizontal, Fat=T=20N.
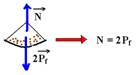
03– Se os garotos aplicarem forças de mesma intensidade, na figura 1 a tração na corda será T e na figura 2, 2T. R- E
04– A força de tração está sobre a corda e no sentido de puxar a garota para a esquerda. A força de atrito é paralela ao apoio horizontal e para a direita, pois é sempre contrário ao movimento ou à sua tendência. R- E
05– Como o caixote está em MRU ele se comporta como se estivesse em repouso e assim, atuam sobre ele apenas seu peso e a reação normal da esteira. R- D
06– Forças que agem sobre a caixa — peso de intensidade P=m.g — P=5.10 — P=50N — tração T=10N e a normal 
(força com que a mesa reage sobre ele).
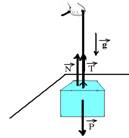
Como a caixa está em equilíbrio, a força resultante sobre ela é nula — P=N+T —50=N+10 — N=40N
07– Colocando as forças que agem sobre o sistema:
– peso do bloco — PB=30.10 — PB=300N —- 
– força de tração no fio —- 
– peso do homem — PH=70.10
PH=700N —- 
– reação normal do chão sobre o homem.
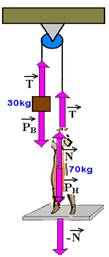
Como o bloco está em equilíbrio — PB=T — T=300N —- o homem também está em equilíbrio — PH=T + N —
700=300 + N — N=400N
I – está errada T=300N II – está errada N= 400N III – está correta N=400N R- C
08– a) parte suspensa – 45 elos — massa de cada elo — P=m.g — 12=m.10 — m=1,2kg — cálculo da massa dos 45 elos por regra de três — m=(45.1,2)/60 — m=0,9kg
b) cálculo do peso dos 15 elos por regra de três — P=(15.12)/60 — P=3N
09– Colocando as forças que agem sobre o sistema:
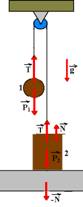
(a) Peso de 1 – P1=m1.g — P1=1,0.10 — P1=10N —- P2=m2,g — P2=4,0.10 — P2=40N — bloco 1 – equilíbrio – FR=0 —
T=P1 — T=10N.
(b) bloco 2 – equilíbrio – FR=0 — P2=T+N — 40=10+N — N=30N.
10– a) peso de cada objeto — P=m.g — P=0,050.10 — P=0,5N — n=5,80/05 — n=11,6 — n=12 objetos
b) entre o suporte e o primeiro objeto, onde a força de tração é maior.
11–
12-
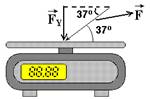
A força adicional aplicada é a parcela vertical de F (FY) que vale — sen37o=FY/F — 0,6=FY/5 — FY=3N. Assim, uma massa de 1,5kg que pesa 15N, passará a pesar 18N e terá massa de 1,8kg. R- D
13– Sobre o bloco C agem os pesos de A e B, ou seja, atuam comprimindo-o para baixo como sendo uma única força de 30N + 60N=90N. É claro que o bloco C reage sobre o B com uma força de mesma intensidade, mas de sentido contrário. R- 90N
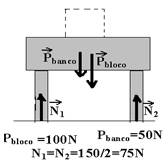
14– A força peso do sistema (20N+40N=60N) está localizada em seu centro de massa que está trocando com a mesa força de 60N, caso contrário, o sistema cairia. Seria como se você colocasse o sistema de peso 60N sobre uma balança, conforme a figura abaixo.
A balança marcaria o peso dos dois blocos, ou seja, 60N.
15– a) Além da força 
, exercida pelo menino, atuam sobre a caixa o peso 
, exercido pelo centro da Terra, a força horizontal de atrito
, e a força vertical 
, ambas exercidas pelo solo.
b) |P|= mg = 80.10 = 800 N; F=60N
Se a caixa não se move, o bloco está em equilíbrio estático e a força resultante sobre ele é nula.
na vertical — N=P — N=800N na horizontal — F=Fat — Fat=60N
16– Qualquer corpo no espaço, em movimento de subida ou descida vertical, obliquo, etc.,desprezando-se a resistência do ar, está sujeito sempre à força resultante que é o peso e à aceleração que é a da gravidade, tendo ambos direção vertical e sentido para baixo. R- B
17– Qualquer corpo no espaço, em movimento de subida ou descida vertical, obliquo, etc.,desprezando-se a resistência do ar, está sujeito sempre à força resultante que é o peso e à aceleração que é a da gravidade, tendo ambos direção vertical e sentido para
baixo. R- A
18– Qualquer corpo no espaço, em movimento de subida ou descida vertical, obliquo, etc.,desprezando-se a resistência do ar, está sujeito sempre à força resultante que é o peso e à aceleração que é a da gravidade, tendo ambos direção vertical e sentido para
Baixo e o vetor velocidade é sempre tangente à trajetória, em cada ponto.. R- C
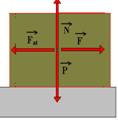
19– Quanto maior a intensidade da força de compressão 
trocada entre a caixa e o solo, maior será a força de atrito. A força que torna a caixa mais “leve” é a da alternativa C.
20– As forças que a caixa e o homem trocam com a superfície são a normal e a força de atrito . Sua soma vetorial nos fornece a
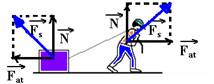
força resultante (
) sobre a caixa e sobre o homem. R- C
21– C
22– Colocando a força 
no centro do bloco e decompondo-a na vertical, teremos:
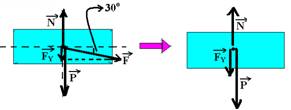
FY=F.sen30o — FY=10.0,5 — FY=5N – parcela de F que comprime o bloco contra o apoio. Como o bloco está em equilíbrio vertical (não sobe nem desce) a força resultante na vertical é nula, ou seja, N=FY + P — N=5 + 12 — N=17N.
23– E
24– Pelo enunciado, a força de intensidade 10N é transmitida pelo cabo até a vassoura de peso P=m.g=0,4.10 = 4N, conforme a figura:
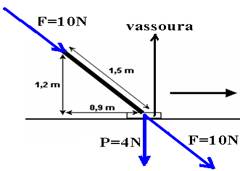
Mas, a força que comprime o piso é a parcela vertical de 10N, que vale:
FY=F.sena = 10.(1,2/1,5)=10.0,8=8N — FY=8N.
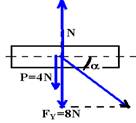
Como a vassoura está em equilíbrio vertical, a intensidade da força resultante nessa direção deve ser nula, ou seja:
N = FY + P — N= 8 + 4 — N=12N
25– Como despreza-se os atritos, sobre ele não surgem forças horizontais, apenas as verticais que são o peso e a força de contato entre ele e a superfície horizontal. Essas forças tem sentidos contrários com a parte esquerda do brinquedo descendo e a direita subindo. R- D
26– Se não existe os efeitos do ar, a força que age sobre a bola é o seu peso, vertical e para baixo. R- E
27– a) Sobre o imã M2 agem, seu peso vertical e para baixo, de intensidade P=m.g=0,03.10 — P=0,3N e a resultante da ação das forças
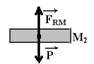
magnéticas de M1 e M3 sobre ele, de intensidade FRM=P=0,3N, vertical e para cima, pois M2 está em equilíbrio.
b) A balança vai marcar a soma das massas de todo sistema, ou seja, (30+90+30+30) = 180g
28– Continuará indicando os mesmos 70kg, pois se a sombrinha comprimir a balança com uma força adicional, a balança reagirá sobre ela com força de mesma intensidade (princípio da ação e reação). R- C
29- a) Indica a intensidade da força de tração no fio onde cada dinamômetro está inserido, ou seja, 5N.
b) Sobre a massa M temos agindo seu peso P (para baixo) e a tração T=5N (para cima). Como M está em repouso, P=T=5N.
P=m.g — 5=M.10 — M=0,5kg.
30– B
31– a) m=20.10-3g=2.10-2.10-3 — m=2.10-5kg — P=m.g — P=2.10-5.10 — P=2.10-4N
b) A força de compressão entre o suporte B e o apoio (N=4.10-2N) equivale a duas vezes o peso total (Pf) das formiga, pois, ao mesmo tempo que A ficou Pf mais leve, B ficou Pf mais pesado.
Pf=peso total das formigas = (número de formigas).(peso de uma formiga) — Pf = n.2.10-4
4.10-2 = 2.(n.2.10-4) — n = 4.10-2/4.10-4 — n = 100 formigas
32– Sobre a pessoa agem as forças — peso — P=m.g — P=68.10 — P=680N, vertical e para baixo. Força que a balança exerce sobre a pessoa — N1=650N, vertical e para cima. Força que a bengala exerce sobre a pessoa — N2=680 – 650 — N2=30N, vertical e para cima. Observe que P=N1 + N2.
a) 30N e para cima
b) 650N, vertical e para cima.
33- A força normal que é trocada entre o patinador e a superfície da rampa é perpendicular à rampa em cada ponto conforme você
pode observar na figura — R- C
34- A força de atrito é tangente à trajetória em cada ponto e contrária ao movimento — a força peso é vertical e para baixo — a força centrípeta tem direção radial e é dirigida para o centro da circunferência — R- E
35- 01. Falsa — após abandonar a mão a única força que age sobre a laranja é a força gravitacional (peso), contrária à subida, que faz com que sua velocidade diminua.
02. Falsa — na altura máxima a velocidade é nula, mas a força peso continua agindo durante todo o movimento.
04. Verdadeira — veja 01 e 02.
08- Falsa — veja as justificativas anteriores.
16- Verdadeira — veja teoria
R- (4 + 16)=20
36- Ele está em MRU (equilíbrio dinâmico) e a resultante de todas as forças que agem sobre ele é nula — R- A
37-
I. Falsa — elas possuem a mesma intensidade mas não constituem par ação e reação, pois são aplicadas no mesmo corpo e se anulam.
II. Correta — a força normal sobre o livro é a força que ele troca com a superfície da mesa (ação e reação) e a força peso é a força que o livro troca com o centro da Terra (ação e reação).
III. Falsa — é uma força de contato entre o livro e a mesa e não uma força gravitacional que é uma força de campo (ação à distância).
IV. Correta — a força normal tem a mesma origem que a de atrito — Fat=μ.N — N=Fat/μ, onde μ é constante para as duas superfícies em contato — a força de atrito se origina, de forças interatômicas, ou seja, da força de interação entre os átomos, portanto sua origem é de natureza eletromagnética, e deve-se à interação entre as nuvens eletrônicas dos átomos localizados nas zonas de contacto entre os corpos — essas superfícies estão bem próximas e, nas regiões de contacto os materiais ficam “soldados” criando pontos de aderência ou colagem (ou ainda solda) entre as superfícies e os picos aderem uns aos outros em virtude das forças de coesão inter-moleculares — no estudo dos fluídos as interações que dão origem à viscosidade e ao atrito fluidodinâmico também são de origem eletromagnética.
R- C.
38-
Colocando as forças que agem sobre cada elefantezinho — considerando o sistema em equilíbrio a intensidade da força
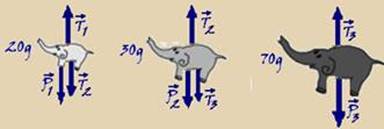
resultante sobre cada um deles é nula (FR=0) — T1=P1 + T2 — T2=P2 + T3 — T3=P3 — T1=P1 + P2 + P3 — T2=P2 + P3 — T3=P3 — T1=0,02.10 + 0,03.10 + 0,07.10 — T1=1,2N — T2=0,03.10 + 0,07.10 — T2=1,0N — T3=0,07.10 — T3=0,7N — R- A