Tipos de Energia – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Tipos de Energia
01– Vo=36km/h/3,6 – Vo=10m/s — a=-4m/s2 (freando) — V=0
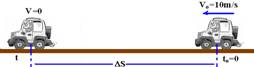
a) V=Vo + a.t — 0=10 -4.t — t=2,5s
b) DS=Vo.t + a.t2/2=10.2,5 – 4.(2,5)2/2 — DS=12,5m
c) Como as forces peso ![]() e a normal
e a normal ![]() se anulam, a força resultante sobre o carro é a força aplicada pelo freio
se anulam, a força resultante sobre o carro é a força aplicada pelo freio ![]() e contrária ao movimento
e contrária ao movimento
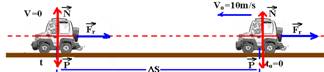
W=Ecf – Eci=mV2/2 – m.Vo2/2=800.02/2 – 800.102/2=0 – 40.000 — W=- 40.000J (negativa, pois o carro está freando e dissipando energia cinética)
02- W=área=b.h/2=10.20/2 — W=100J — W=Ecf – Eci=m.V2/2 – m.Vo2/2=2.V2/2 – 0 — 100=V2 — V=10m/s
03- W=Ecf – Eci=1.02/2 – 1.82/2 — W= -32J R- D
04- W=0,2.(0,6))2/2 – 0,2.(0,3)2/2=0,036 – 0,009=0,027 — W=2,7.10-2J R- A
05- R- B (veja teoria)
06- Vo=30m/s — V=0 — W=m.V2/2 – m.Vo2/2=0 – 1000.900/2= -900.000/2=-450.000J R- C
07- m=50g=50.10-3=5.10-2kg – DS=0,5cm=5.10-1.10-2=5.10-3kg – Vo=2.102m/s – V=0 — O trabalho realizado pela fibra de kevlar é igual ao trabalho realizado pela força resultante resistiva da fibra que se opõe à bala, parando-a.
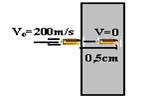
W=0 – 5.10-2.(2.102)2/2=5.10-2.4.104/2=20.102/2 — W=1.103J — W=F.d.cosa — 103=F.5.10-3.cos180o — 103=F.5.10-3.(-1) — F= – 103/5.10-3= – 10.102.103/5 — F= – 2.105N R- A
08- Vo=108km/h=30m/s – V=0 (pára) – m=80kg — W=m.V2/2 – m.Vo2/2= 0 – 80.(30)2/2 — W= – 36.000J R- C
09- m=20g=20.10–3=2.10-2kg – Vo=240m/s – V=0
a) Eci=m.Vo2/2=2.10-2.(240)2/2=2.10 -2.5,76.104/2 — Eci=576J — W=Ecf – Eci=0 – 576 — W= – 576J
b) DS=d=18cm=18.10-2m — W=Fm.d.cos180o — -576=Fm.18.10-2.(-1) — Fm=3.200N
10- R- A (veja teoria
11-R- A (veja teoria)
12- a) h=5.0,3=1,5m — Epf=m.g.h=70.10.1,5=1.050J — Epf=1.050J
b) W=Epi – Epf=0 – 1.050 — W= – 1.050J
c) Não, seria o mesmo, pois o trabalho da força peso não depende da trajetória (a força peso é uma força conservativa).
13- a) W(A)=Epi – Epf=50.10.0 – 50.10.16= 0 – 8.00 — W(A)= – 8.000J
W(B)=Epi – Epf=50.10.0 – 50.10.16= 0 – 8.00 — W(B)= – 8.000J
W(A)/W(B)=1
b) Como as velocidades inicial e final são nulas, a variação de energia cinética também será nula e a variação de energia mecânica será igual à variação de energia potencial gravitacional que é de 8.000J, tanto para Abelardo, quanto para Heloísa.
14- Todas estão corretas – soma=15
15- W=Epi – Epf= 0 – 450.10.3,2= – 2,5.104J (aproximadamente)
16- A energia mecânica é igual a 24/80% = 24/0,8 = 30 J
Esta energia é a energia potencial gravitacional do corpo, E = mgh, então:
mgh = 30
2.10.h = 30
20h = 30
h = 30/20 — h= 1,5 m
17- a) Falsa –W=m.g.h=80.10.5=4.000J
b) Falsa, basta apenas ela subir com qualquer tipo de movimento
c) Verdadeira – W=m.g.h
d) Falsa, existe trabalho, pois houve variação de energia
18- a) d=1g/cm3=103kg/m3 — V=50m3 por segundo — d=m/V — 103=m/50 — m=5.104kg por segundo
b) A energia potencial gravitacional armazenada por m=5.104kg de água numa altura de 160m em 1s, num local onde g=10m/s2 é dada por — Ep=m.g.h=5.104.10.160 — Ep=8.107J
c) Po=W/Dt=4,2.109/60 — Po=7.107W
19- R- A – Observe que o gráfico é de E em função de x2, pois se fosse em função de x seria a alternativa b
20- Quando x=1m, F=500N — F=K.x — 500=K.1 — K=500N/m — Epe=K.x2/2 = 500.(0,6)2/2 — Epe=90J
21- Epe=K.x2/2=10.0,04/2 — Epe=0,2J R- B
22- Epei=K.x2/2=150.(2,0.10-2/2=150.4,010-4/2= 300.10-4J — Epef=150.(2,5.10-2)2/2=468,75.10-4J — W=DEpe=Epei – Epef= 300.10-4 – 468,75.10-4= – 168,75.10-4= – 1,6875.10-2J (negativo, pois o deslocamento é forçado por uma força externa) ou, graficamente —
quando x=2,0.10-2m – F=K.x=150.2.10-2=3N — quando x=2,5.10-2m – F=K.x=150.2,5.10-2=3,75m — colocando esses valores no gráfico F X x, teremos:
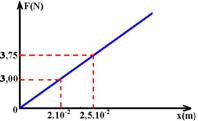
Energia potencial armazenada quando x=2.10-2m — W=Epei=área do triângulo=b.h/2=2.10-2.3/2=3,0.10-2J
Energia potencial armazenada quando x=2,5.10-2m — W=Epei=área do triângulo=b.h/2=2,5.10-2.3,75/2=4,6875.10-2J
∆Epe= W=∆Epe=Epei – Epef=3,0.10 – 4,6875.10-2 = –1,6875.10-2J — ou ainda, pela área do trapézio que representa o trabalho realizado (variação de energia potencial elástica) — W=∆Epe=(B + b).h/2=(3,75 + 3,0).0,5.10-2/2=1,6875.10-2J R-E
23- a) Do enunciado e do gráfico
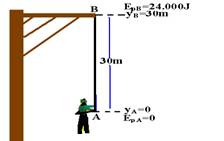
Wde B para A=EpB – EpA=24.000J — 24.000= EpB – EpA=m.g.yB – m.g.yA=P.yB – P.yA — 24.000=P.30 – P.0 — P=800N
Observe no gráfico que a energia elástica só começa a surgir a partir de 20m, quando a corda começa a ser esticada. Assim, Lo=20m
b) Se o comprimento natural da mola é 20m e ela foi deformada até 30m, a deformação é x=30 – 20=10m, e para efetuar essa deformação a energia potencial elástica foi de 24.000J (veja gráfico) — Uelástica=K.x2/2 — 24.000=K.(10)2/2 — K=480N/m
24- 01. Correta — trabalho é a medida da quantidade de energia transferida por uma força ao longo de um deslocamento — em Física, trabalho é transferência de energia, provocando deslocamento.
02. Correta — observe na expressão Ec=mV2/2 que a energia é diretamente proporcional ao quadrado da velocidade e, como V1=4V2 ela ficará 42=16 vezes maior.
04. Correta — energia potencial é energia de posição, dependendo, portanto, de um referencial.
08. Correta — a cada transformação, parte da energia transformada é dissipada, pois não há transformação com 100% de rendimento.
16. Correta — energia cinética provém de outras formas de energia.
R- (01 + 02 + 04 + 08 + 16) = 31
25- (01) Errada. O trabalho da força peso é igual a m g h. A força que provoca rotação é resistência do ar e não o peso.
(02) Correta. Como a folha cai com velocidade constante, pelo princípio da inércia, a resultante das forças sobre ela é nula, ou seja, a força de resistência do ar sobre ela e seu peso têm mesma intensidade.
(04) Correta. Se as velocidades de translação e de rotação são constantes, as energias cinéticas de translação e rotação também o são.
(08) Correta. Como já afirmado, a força que provoca rotação é a de resistência do ar e não o peso.
(16) Errada. A folha está perdendo energia potencial. Como a energia cinética total permanece constante, a energia mecânica está diminuindo.
R- (02+ 04 + 08) = 14
26- Para atingir a altura desejada ele deve ganhar de energia potencial a quantidade ΔEp, com N idas e vindas — ΔEp=mgh-800.3 — ΔEp=2.400J — ΔEp=NE1 — 2.400=N.600 — N=4 — R- C
27-
![]()
E1/E2=10
28- a) Dados: Δx = 6,4 nm = 6,4.10-9 m; d = 100 nm = 100.10-9 m = 10–7 m; b = 9,6.10-39N.m4;
Fc=Fe=b/d4 — Fc=k Δx — k=b/d4.Δx — k=9,6.10-39/10-7.6,4.10-9 — k=0.015N/m
b) Dados: ET = kBT; kB = 1,4 .10-23 J/K; T = 300 K; kB = 0,21 N/m = 2,1 10-1 N/m — Ee=ET — kΔx22=kBT —
Δx=√(2.1,4.10-23.300)/2,1.10-1 — Δx=√8,4.10-21/2,1.10-1 — Δx=√4.10-20 — Δx=2.10-10m — Δx=0,2nm
29- Observe a figura — como o bloco está em equilíbrio, a resultante das forças sobre ele é nula. Ou
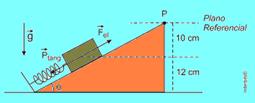
seja, a força elástica é equilibrada pela componente tangencial do peso — Fe=Pp — kx=Psenθ — x=10.0,8/100 — x=8,0.10-2m — como centro de massa do bloco está abaixo de plano referencial, sua energia potencial gravitacional é negativa — soma pedida das energias —
![]() = 0,32 – 1
= 0,32 – 1
![]() = – 0,68 J.
= – 0,68 J.
R- A
30- Em relação a João, as velocidade de Pedro e Paulo são, respectivamente — VPe=0 — VPa=1m/s — EcPe=0 — EcPa=60.12/2 —
EcPa=30J — R- A
R- A
31-

32- Observe nas figuras abaixo as forças que agem em cada uma das partes:
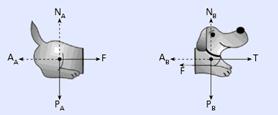
a) Como as partes se movem em movimento retilíneo e uniforme, a resultante das forças em cada uma delas é nula — corpo A — NA = PA — NA = 5 N
F = AA — F = μc • NA — F = 1,5 N — corpo B — NB = PB — NB = 10 N — T = F + AB — T = F + μc • NB —
T = 4,5N
b) A força T é constante –p- trabalho da força T — W = T • Δs • cos α — o ângulo entre a força e o deslocamento é nulo — cos α = 1 — como a velocidade dos corpos também é constante — Δs = v • Δt — W = T • v • Δt — W = 4,5 • 0,1 • 120 —
W = 54 J
c) Do resultado obtido no item a — F = 1,5 N
d) Chamando de δ a deformação da mola — F = k • δ — 1,5 = 10 • δ — δ = 0,15 m — comprimento da mola — x = xo + δ — x = 0,1 + 0,15 — x = 0,25 m ou x = 25 cm
33-

34- A energia potencial independe da trajetória — apenas a III está correta — R- C
35- Ec=mV2/2 — se a massa cai pela metade a energia cinética de 1 também cai pela metade — se V1=4V2 — a energia cinética de 1 fica 42=16 vezes maior — Ecx16/2=8Ec — R- C
36- Como as perdas de energia por dissipação são desprezadas, a energia mecânica total do sistema estudante + corda elástica é conservada. No início, não há energia cinética do estudante, que inicia o salto a partir do repouso, nem energia potencial elástica (corda sem tensão). No ponto mais baixo do salto, também não há energia cinética do estudante, que apresenta velocidade nula. Além disso, a energia cinética da corda é desprezada. Assim, a energia potencial elástica da corda nesse ponto é igual ao módulo da variação de energia potencial gravitacional do estudante, isto é, PH 40 = 24.000 J — = 600. R- B
37- Ep=mgh — M andares — Ep=Mmgh — N pessoas — Ep=NMmgh — duas vezes ao dia — Ep=2NMmgh — R- C
38-(ENEM-MEC-011)
Pode-se definir o Segundo Princípio da Termodinâmica da seguinte maneira: “É impossível obter uma máquina térmica que, operando em ciclos, seja capaz de transformar totalmente o calor por ela recebido em trabalho” — sempre haverá energia dissipada pelo motor — R- C.
