O Princípio Fundamental da Dinâmica ou Segunda lei de Newton – Resolução

Resolução comentada dos exercícios de vestibulares sobre o Princípio Fundamental da Dinâmica ou Segunda lei de Newton

 

 

01-

a) Na vertical  —  35N-20N=15N (para baixo)              Na horizontal  —  40N-20N=20N (para a direita)

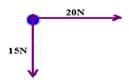
Efetuando a adição vetorial

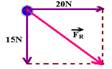
Aplicando Pitágoras  —  F_R² = (15)² + (20)²  —  F_R = 25N

F_R = m.a  —  25=0,5.a  —  a=50m/s²  —  a direção e sentido de a é sempre a mesma que de F_R

b) Quando as três forças tiverem a mesma intensidade e o ângulo entre elas for de 120^o a força resultante é nula e consequentemente a aceleração também será, ou seja, .

c) Somando vetorialmente as duas forças de 24N e aplicando a lei dos cossenos:

 

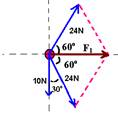
F₁² = (24)² + (24)² + 2.24.24.cos120^o  —  F₁² = (24)² + (24)² + 2.(24)².(-1/2)  —  F₁=24N

Então teremos:

 

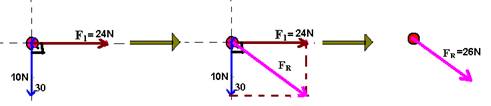
Aplicando Pitágoras  —  F_R² = (24)² +(10)²  —  F_R=26N

 

02-

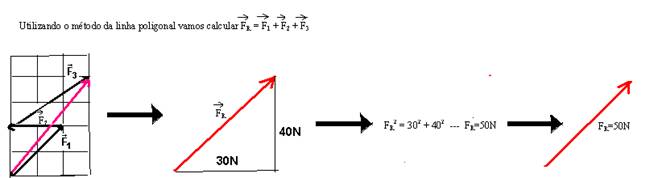
03- Na vertical  —  3N para cima.  —  Na horizontal  —  4N para a direita  —  Aplicando Pitágoras  —  5N  —  R- A

 

04- D

05- A  

06- A alternativa a é falsa, pois 2F=2m.2a  —  2F=4ma  — F=2ma

A alternativa b é correta, pois 2F=2m.a  —  F=ma

A alternativa c é falsa, pois F=2m.2a  —  F=4ma

A alternativa d é falsa, pois 2F=m.a/2  —  F=(ma)/4

A alternativa e é falsa, pois 3F=2m.a/2  —  F=(ma)/6

07- Entre 0 e 2s, a velocidade é constante e a trajetória reta, portanto trata-se de um MRU (equilíbrio dinâmico) e a força resultante é nula. Entre 2s e 4s, o movimento é desacelerado e a aceleração vale  —  a=(V – V_o)/t – t_o  —  a=(0-10)/(4-2)

—  a= – 5m/s²  —  a força resultante é constante e vale F=m.a  —  F=2.(-5)  —  F= -10N  —  como o exercício pede o módulo   —  F=10N.  R- A

08- Da equação fornecida  —  a=6m/s².  —  F=m.a  —  F=5.6  —  F=30N

09- V=V_o + a.t  —  0=20 + a.0,10  —  a= -20/0,10  —  a= – 200m/s²  —  F=m.a  —  F= -0,40.200  —  F= -80N  —  módulo  —  F=80N

10- Observando a figura abaixo, concluímos que e que, .

 

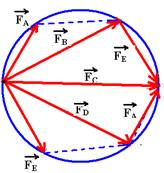
Como a força resultante é a soma vetorial de todas as forças temos   —    

  —    —  F=3.10  —  F=30N

11- Decompondo cada força na horizontal  —  —    —  

Resultante na horizontal  —    —  F_H=4N

Decompondo cada força na vertical

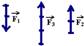
Resultante na vertical:

Então teremos: 

 

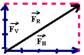
Aplicando Pitágoras  —  F_R=5N

12-1^o movimento  —  F=ma  —  m=F/a           2^o movimento  —  4F=ma₁  —  m=4F/a₁  —  F/a=4F/a₁  —  a₁=4a

1^o movimento  —  V=V_o + a.t  —  5=0 + a.t  —  a.t=5

2^o movimento  —  V₁=V_o + a₁.t  —  V₁=5 + 4.a.t  —  V₁=5 + 4.5  —  V₁=25m/s   R- C

13- F=ma  —  3.000=m.1,5  —  m=2.000kg  —  I – correta   —   II – falsa

V=V_o+a.t  —  V=0+1,5.4  —  V=6m/s  —  III – correta

DS=V_o.t + a.t²/2  —  DS=0.2 + 1,5.4/2  —  DS=3m  —  IV – falsa

V – correta  —  m=F/a=constante  — F e a são diretamente proporcionais

R – C

14- Observe na segunda lei de Newton que: F=m.a  —  a=F/m  —  a e m são inversamente proporcionais  —  R- A

15- m₁=3m₂/4  —  a₂=a₁=4m/s²  —  F₂=m₂.a₂  —  m₂=8/4  —  m₂=2kg  —  m₁=(3.2)/4  —  m₁=1,5kg  —  F_o=m_1.a₁  —  F_o=1,5.4  —  F_o=6N.

16- Cálculo da aceleração do cubo de lado L  —  ΔS=V_ot + at²/2  —  80=0 + a.10²/2  —  a=1,6m/s²  —  como o novo cubo é idêntico ao anterior, eles possuem a mesma densidade  —  d=m/v  —  d=m/(L/2)³  —  observe na expressão anterior que, se o volume fica 8 vezes menor, a massa também ficará 8 vezes menor, pois a densidade é constante  —  F=ma  — 

Sendo a força F a mesma, se a massa fica 8 vezes menor a aceleração deverá ficar 8 vezes maior  —  nova aceleração  —  a=8×1,6  —  a=12,8m/s²  —  ΔS’=V_ot + at²/2=0 + 12,8.10²/2  —  ΔS’=640m  —  R- C

17- R- A  —  Princípio da inércia

18- I. Correta  —  Princípio da Inércia

II. Correta  —  se ele sobe a força resultante sobre ele tem que ser para cima.

III. Correta  —  Correta  —  quanto maior a força de compressão com o solo, maior será a força de atrito

R- E

19- Se existem forças agindo sobre um objeto ele não está necessariamente acelerado o que ocorre somente se a intensidade da força resultante for diferente de zero  —  mas, se essas forças se anularem ele estará em repouso ou em MRU  —  R- C

20- a) As forças que agem na massa pendular são o peso e a tração.

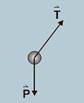
b) Como o movimento é retilíneo, a componente vertical da resultante é nula  —   T_y=P  —  A resultante é então na direção

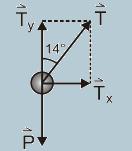
horizontal  —  F_R= T_X  —   como o vagão parte do repouso, ele acelera no sentido da resultante, ou seja, para a direita  — 

c) Do princípio fundamental da dinâmica  —  F_R = m a  —  T_X = m a_max  —  como, na vertical, a componente da resultante é nula  —  T_y = P = m g  —  tg14^o=T_X/T_y=m.a_Max/m.g  —  0,25=a_max/10  —  a_max=10.0,25  —  a_max=2,5m/s²

21- (I) Incorreta  —  o trailer é uniformemente acelerado apenas no intervalo 0 a t₁, onde a resultante tem intensidade constante.

(II) Correta  —  até o instante t₄ há uma força resultante acelerando o trailer, fazendo sua velocidade aumentar.

(III) Correta  —  se a resultante é nula, o movimento retilíneo e uniforme. 

R- C

22-  Intensidade da resultante dessas forças  —  F_R²=F₁² + F₂²  —  F_R=√(2² + 1,5²  —  F_R=2,5N  —  pelo princípio fundamental da dinâmica  —  F_R=ma  —  2,5=2.a  —   a=1,25m/s²  —  R- A

23- F₁=m₁.a₁  —   F₁ = 2 (3)  —  F₁ = 6 N  —  F₁=F₂=F = m₂ a₂  —  6 = 1 a₂  —  a₂ = 6 m/s² —  R- D

R- D

24- A distância percorrida em um diagrama de velocidade versus tempo é dada pela área sob a linha de gráfico  —  aproximando esta figura para um triângulo retângulo  —  d=base.altura/2=1,4.1/2  —  d=0,7m  —  R- A

25- a=(V – V_o)/(t – t_o)=(0,4 – 0,8)/0,8 – 0,4  —  a=-1m/s²  —  pela segunda lei de Newton  —  F=ma=2.(-1)  —  F=-2N  —  R- A

26- O vetor velocidade é tangente à trajetória e é vertical e para cima na subida e vertical e para baixo na descida  —  a aceleração da gravidade  tem sempre direção vertical e sentido para baixo  —  a força de atrito  tem direção do movimento e sentido contrário a ele, ou seja, ao vetor velocidade  —  R- A

27- A força resultante sobre o elevador é nula (P=T) se ele estiver subindo ou descendo em movimento retilíneo e uniforme ou em repouso  — R- D

28- Se o avião acelera para frente, por inércia, o corpo pendurado no fio tende a ficar parado em relação à pista e, portanto, vai para trás em relação ao avião  —  o fio inclina-se para a esquerda  —  a aceleração do avião será dada por  —  a = g.tan 25^o = 10.0,47  — 

a = 4,7 m/s²  —  R- A

 

29-

Em todo gráfico V x t a distância percorrida é numericamente igual à área hachurada, entre 0 e 5s, da figura abaixo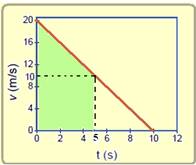  

— ∆S=área  —  ∆S=(B + b).h/2=(20 + 10).5/2  —  ∆S=75m  —  cálculo da aceleração do carro pelo gráfico  —  a=(V – V_o)/(t – t_o)=(0 – 20)/(10 – 0)  —  a=- 2m/s²  —  força resultante  —  F_R=m.a=1000.(-2)  —  F_R=- 2000N em módulo F_R=2000N  —  R- C.

 

 

30- Para calcular a intensidade da força resultante que age sobre a partícula cósmica você pode decompor as forças nas direções norte e leste  —  observe na sequência abaixo que a intensidade da força resultante é de 1N no sentido leste  —

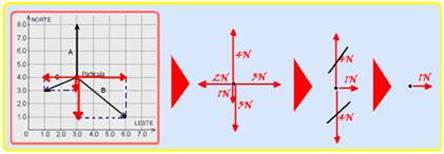
Como a velocidade inicial da partícula tem intensidade V_o=1200m/s do norte para o sul e a força resultante sobre ela tem intensidade 1N do oeste para leste, o movimento da partícula tem as características de composição de dois movimentos, um no sentido leste e outro no sentido sul (veja figura)  —  no sentido leste, a projeção da velocidade inicial é nula V_oL=0 e ela se desloca sob ação de uma força resultante de valor F_R=1N e com aceleração  —  F_R=m.a  —  1=2.10^-3.a  —  a= 500m/s²  —  sua velocidade nessa direção após t=1s terá intensidade  —  V_L=V_oL + a_L.t=0 + 500.1  —  V_L=500m/s  —  no sentido sul ela será lançada para baixo com V_oS=1200m/s, acelerando com aceleração da gravidade g=10m/s²  —  após t=1s, sua velocidade nessa direção será  —  V_S=V_oS + g.t=1200 + 10.1=1210m/s  —

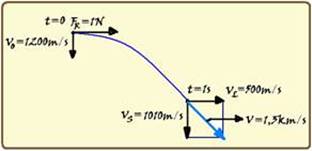
 observe na figura que essas duas velocidades são perpendiculares e, aplicando Pitágoras você obterá V² = V_L² + V_S²=(500)² + (1210)²  —  V=√(1714100)  —  V=1309m/s=1,3km/s  —  R- A.

31-

Pelo princípio da inércia, se as forças deixarem de atura, a força resultante sobre ela será nula e, após esse innstante, por inércia, ela seguirá em MRU com velocidade constante de 1,3km/s  —  observe na resolução do exercício anterior (08) que, antes de 1s a trajetória era parabólica  —  R- D.

 

32-

Se o deslocamento ocorresse com velocidade constante a força resultante sobre a caixa seria nula  —  nesse caso, a

força que a pessoa exerce sobre a caixa tem que ter a mesma intensidade que a força de atrito  —  note que a força que a pessoa exerce sobre a caixa  tem a mesma intensidade que a força que a caixa exerce sobre a pessoa (princípio da ação e reação)  —  R- A

33-

Nesse caso, como existe aceleração a resultante das forças sobre a caixa é diferente de zero  —  F_R=m.a  — como a

caixa se desloca na mesma direção e sentido que F_p  —  F_p – F_a=m.a  —  F_p > F_a  —  note que a força que a pessoa exerce sobre a caixa  tem a mesma intensidade que a força que a caixa exerce sobre a pessoa (princípio da ação e reação)  —  R- C

 

Voltar para os Exercícios