Potência de uma força – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Potência de uma força

 01-Maior consumo – P_o=5.10³W  —  ∆t=2h  — P_o=W(energia consumida)/∆t — 5,10³=W/2  —  W=10.10³W  —  W=10kW R- B

02- Velocidade constante – a força que está puxando é igual ao peso da caixa d’agua  —  P=m.g=66.10  —  P=660N  —  W=P.h=660.18  —  W=11.800 J  —  P_o=W/Dt=11.800/120  — P_o=99W

03- O trabalho do peso independe da trajetória e vamos calculá-lo pela altura  —  h=0,150.60  —  h=9m  —  W=m.g.h  —

W=80.10,9=72.10²  —  W=7,2.10³ J  —  P_o=W/Dt=7,2.10³/120  — P_o=60,0W  R- A

04- Regra de três  —  1cal – 4,2 J  —  100.000cal  —  x J  —  x=4,2.10⁵ J=W (energia)  —  P_o=W/∆t  —  60=4,2.10⁵/∆t  — ∆t=4,2.10⁵/60  —  ∆t=0,07.10⁵=7.000s/60=116,7min  —  R- C

05- Na horizontal e na subida a esteira se move com velocidade constante de 1,5m/s, ou seja, em 1s ela percorre 1,5m e, pela figura,

Observamos que ela transportou, na horizontal e na vertical ela transportou 1,5 caixas por segundo.1 caixa – 80kg  —  1,5 caixas —  m=80.1,5  —  m=120kg, que é a massa que a esteira na parte inclinada deve elevar de 5m em cada 1s com velocidade constante de 1,5m/s.

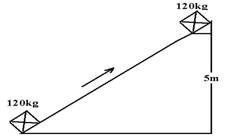
Cálculo do trabalho pela altura  —  W=m.g.h=120.10.5  —  W=6.000J – energia consumida para elevar uma massa de 120kg de 5m.  —  P_o=W/∆t=6.000/1  — P_o=6.000W – energia consumida para elevar uma massa de 120kg de 5m em 1s.. 

06- com a chave na posição inverno – P_o=W/∆t  —  6.000=W_i/30.0,5  —  W_i=90.000W=90kW (energia elétrica consumida) com a chave na posição verão – P_o=W/Dt  —  4.000=W_v/15  —  W_v=60.000W=60kW(energia elétrica consumida)

economia – 90kW – 60kW= 30kW R-B

07- Energia consumida em 1 mês (30 dias) – W=30.3.000kcal=9.000.k.(4J)  —  W=360.000KJ=360.000.000J (energia em Joules, consumida em 1 mês)  —  regra de três  — 1kWh – 3.600.000J  —  x kWh – 360.000.000J  —  x=100kWh R- C 

 

08- Potência para elevar o peso do elevador vazio à altura de 32m em 40s  —  P_oe=W/Dt=m.g.h/Dt=370.10.32/40  —  P_oe=2.960W

Potência para elevar uma pessoa à altura de 32m em 40s  —  P_op=W/Dt=m.g.h/Dt=70.10.32/40  —  P_op=560W

A potência do motor menos a potência para elevar o elevador vazio nos fornece a potência que sobra para elevar o número de pessoas  —  8.500 – 2.960=5.540W  —  regra de três  —  1 pessoa – 560W  —  n pessoas – 5.540W  —  n=5.540/560=9,89  — 

n= 9 pessoas  R- C

09- d=m/V  —  1.000=m/700  —  m=700.000kg (massa de água que cai de uma altura de 120m em cada 1s)  — P_o=m.g.h/Dt  —  P_o=700.000.10.120/1=840.000.000W  —  P_o=840.000kW  —  P_o=8,4.10⁵kW

10- P_o=m.g.h/∆t  —  512.000.000=m.10.120  —  m=512.10⁶/12.10²  —  m=42,7.10⁴=437.000kg  + 0,1 x437.000=480.700kg

Considerando a densidade da água 1kg/L, teremos que uma massa de 1kg ocupa um volume de 1L de água  — R- E

11- Do 8^o ao 12^o – 4 degraus  —  h=4.0,18=0,72m  —  P_o=m.g.h/∆t=70.10.0,72/2,8  — P_o=180W  R- A

12-V=280m³=280.10³dm³=280.10³L=280.10³kg  —  m=28.10⁴kg  —  P_o=m.g.h/∆t=28.10⁴.10.160/1=2.816.10⁶  —   P_o=448.10⁶ P_o=0,448.10⁸ W 

13- Considerando que o volume de 1L de água possui massa de 1kg  —  V=26m³=26.10³dm³=26.10³ L  —  m=26.10³kg  —  a transposição é a elevação da água do rio São Francisco da altura de 315m (elevatória 1) até 475m (elevatória 4) —  h=475 – 315=160m  —  P₀=m.g.h/Dt=26.10³.10.160/1  —  P_o=416.10⁵W=41,6.10⁶W  —  R- C 

14- a) uma turbina de potência 680.10⁶W foi paralisada durante 3h —  P_o=W/∆t  —  680.10⁶=W/3  —  W=2.040.10⁶=2.040.000kWh (energia elétrica não fornecida por Itaipu durante 3h)  —  regra de três  —  1 domicílio – 4kWh  —  N domicílios – 2.040.000kWh

— 4N=2.040.000  —  N=510.000 municípios

b) d=m/V  —  10³=m/600  —  m=600.10³  —  m=600.000kg

c) P=m.g.h=6.10⁵.10.120=720.10⁶W  —  P=720MW

15- Por dia uma pessoa utiliza 30L  —  4pessoas  —  4.30L  —  120L  —  em um mês 4 pessoas utilizarão – V=30.120=3600L  — m=3.600kg  —  m=3.600.000g  —   c = 4,19 J/g°C  —  ∆t=30^oC  —  equação fundamental da calorimetria – Q=m.c.∆t  —  Q=3.600.000.4,19.30  —  Q=W=452.520.000J  —  lembrando que 1kWh=1.000W.3.600s  —  1kWh=3.600.000J  — regra de três  —  1kWh – 3.600.000W  —  x kWh – 452.520.000  —  x=W=452.520.000/3.600.000  —  W=125,7kWh  —  Considerando que a água no tanque, de 200 litros, libera 0,30 kWh/litro, a cada mês, tem-se que a perda é de  200×0,30=60 kWh.

Assim os painéis solares terão que fornecer, por mês, 125,7 + 60 = 185,7 kWh  —  regra de três  —  se 1m² metro quadrado de painel, no mês, fornece 60 kWh, 187,5kWh serão fornecidos por x m²  —  60.x=185,7  —  x=3,1m² de superfície de painéis solares.

16- W=(B + b).h/2 + b.h=(3.10³ + 2.10³).100/2 + 50.3.10³=250.10³ + 150.10³  — W=400.10³=4.10⁵J

17- Se está com velocidade constante (equilíbrio estático), a intensidade da força  com que o motor puxa o bloco deve ser igual à intensidade da força de atrito .

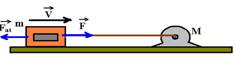
F=F_at=mN=mP=mmg=0,1.500.10  —     F=500N  —  P₀=F.V=500.0,5  —  P_o=250N

18- a) P_o=W/∆t  —  300=W/1800  —  W=540.000J (energia “gasta” pelo atleta em joules)  —  regra de três  —  1 cal  –  4,2J  —  X cal  –  540.000J  —  4,2X=540.000  —  X=12,9.10⁴=1,29.10⁵ cal.

b) V=∆S/∆t=10.000/1.800  —  V=50/9m/s  —  P_o=F.V  —  300=F/50/9  —  F=54N

19- V=72km/h/3,6=20m/s  —  P_o=200.000W  —  P_o=F.V  —  200.000=F.20  — F=10.000N  R- A

20- Como a velocidade é constante a força motora é a força de atrito  —  F=F_at  —  P_o=F_at.V  —  25.000=F_at.80/3,6   —  F_at=1.125N  —  R- A

21- Potência utilizada para elevar um bloco de m=75kg a uma altura de 1m   — P_o=F.V=P.V =m.g.V =75.10.1  —  P_o=750W

Potência desenvolvida pelo carro  —  P₀=F.V=P_p.V=mgsenq.V=1.000.10.0,1.15  —  P₀₌15.000W  —  regra de três  — 1 CV – 750W  —  X CV – 15.000W  —  X=15.000/750  —  X=20CV  R- A

22- a) Como ele sobe com velocidade constante (equilíbrio dinâmico – F_R=0), F₁=P=m.g=5.000.10  —  F₁=5,0.10⁴ N

b) Como tem aceleração  —  F_R=m.a  —  F_2­  – P=m.a  —  F₂ – 50.000=5.000.5  —  F₂=50.000 + 25.000  —  F₂=7,5.10⁴N

c) P_o=F₂.V  —  150.10³=7,5.10⁴.V  —  V=2,0m/s

d) A velocidade máxima ocorre quando a força motora é o peso (P=50.000N) e a potência é a máxima do motor (P_o=150.000W)

P_o=P.V  —  150.000=50.000.V  —  V=3,0m/s.

23- a) Situação 1  —  V_o=60m/s – constante – equilíbrio dinâmico – força resultante nula – F_R=0

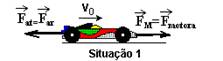
P₁=F_M.V  —  120.000=F_M.60  —  F_M=2.000N  —  como V=constante (equilíbrio dinâmico) – F_M=F_ar=F_R=2.000N 

b) Situação 2  —  V constante – força resultante nula – motor desligado F_M=0

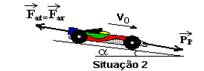
P_P=F_ar=m.g.sena=800.10.sena  —  ms, F_ar é a mesma da situação 1 (2.000N)  —  2.000=8.000sena  —  sena=0,25 

c) Situação 3  —  V constante – força resultante nula

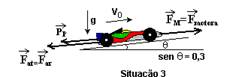
Forças que agem na direção do movimento  —  P_p=m.g.senq – parcela do peso, paralela à superfície do plano inclinado  —  P_P=800.10.0,3  —  P_P=2.400N  —  F_ar – força de resistência do ar, constante e igual a 2.000N  —  F_M – força motora  —

Como a resultante é nula – F_M=P_P + F_ar  —  F_M=2.400 + 2.000  —  F_M=4.400N  —  P_o=F_M.V=4.400.60  —  P_o=264kW

24- Colocando as forças que agem sobre os sistema:

 

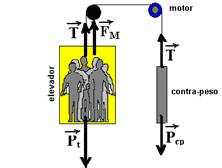
P_t – peso total do elevador  —  P_t=(200 + 420).10  —  P_t=6.200N  —  P_cp=220.10  —  P_cp=2.200N  —  Como tanto elevador como contra peso estão com velocidade constante, estão em equilíbrio dinâmico e a força resultante sobre eles é nula  —  contra peso  —  P_cp=T  —  T=2.200N  —  elevador  —  P_t=T + F_M  —  6.200=2.200 + F_M  —  F_M=4.000N  —  P_o=F_M.V  —  P_o=4.000.0,5  — 

P_o=2.000W=2kW

25- Colocando as forças:

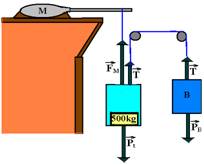
Elevador – peso total – P_t=1.300.10  —  P_t=13.000N  —  contra peso B – P_B=m.g=800.10=8.000N  —  P_B=8.000N 

a) ambos estão em equilíbrio dinâmico com força resultante nula  —  contra peso – P_B=T  —  T=8.000N  —  elevador – Pt=F_M + T  —  13.000=F_M + 8.000  —  F_M=5.000N  —  P_o=F_M.V  —  P_o=5.000×1  —  P_o=5kW

b) contra peso B – F_R=m.a  —  P_B – T=m_B.a  —  8.000 – T=800.0,5  —  T=7.600N  —  elevador – F_R=m_e.a  —  F_M + T- P_t=1.300.0,5  —  F_M + 7.600 – 13.000=650  — F_M=6.050N 

26- Trata-se de uma função de 1^o grau (gráfico é uma reta) de equação F=F_o + k.V, onde k é a constante de proporcionalidade  — 

F_o=50N (constante)  —  F=50 + k.V  —  quando V=30m/s – F=20N  —  20=50 + k.30  —  k= -1N.s/m (constante)  —  a função é F=50 – 1.V  —  quando V=20m/s  —  F=50 -1.20 – F=30N  —  P_o=F.V=30.20  —  P_o=600W  R-B

27- P_t=1.000W  —  a potência útil (P_u) é aquela que realiza trabalho – P_u=W_u/∆t=3200/4=800  —  P_u=800W  —  h=P_u/P_t=800/1000=0,8  —  h=80 %  R-D                      

28- P_u=8.640/60=144W  —  h=144/200=0,72=72 %

29- a) velocidade constante,  a força motora é igual à força peso e o trabalho do peso, que é uma força conservativa independe da trajetória e vamos calcular esse trabalho em função da altura, no deslocamento de C até B.

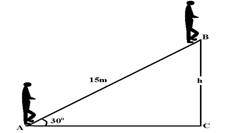
Sen30^o=h/15  —  h=7,5m  —  W=m.g.h=80.10.7,5  —  W=6.000J

b) P_o=W/Dt=6.000/30  —  P_o=200W                c) h=P_u/P_t=200/400=0,5=50 %  — h=50 %

30- P_u=P.h/Dt  —  125=50.10/Dt  —  Dt=4,0s  R- E

31- R- A – veja teoria

32- Cálculo do trabalho útil  —  W_u=F.d.cosa=1800.400.1  —  W_u=7,2.10⁵J  —h=W_u/W_t  —  0,45=7,2.10⁵/W_t  —  W_t=7,2.10⁵/0,45  —  W_t=1,6MJ  R-E

33- Do enunciado, a potência total P_t é dada por P_t=299cv x 740=221.260W  —  cálculo da aceleração do carro quando sua velocidade passa de 0 a 28m/s em 7,5s – V=V_o + a.t  —  28=0 + a.7,5 – a=3,7m/s²  —  cálculo do deslocamento DS=d=v_o.t + a.t²/2=0 + 3,7.(7,5)²/2  —  d=104m  —  cálculo da força motora – F_M=m.a=2.400.3,7  —  F_M=8.880N  —  cálculo do trabalho útil realizado pelo motor nesse deslocamento – W_u=F_M.d.cos0^o=8.800.104.1  —  W_u=915.200J  —  cálculo da potência útil – P_u=W_u/Dt  — P_u=915.200/7,5  —   P_u=122.027W  —  P_u/P_t=122.027/221.260  —  P_u/P_t=0,55  R-C

34- a) Considerando a densidade da água 1kg/L – 1m3 = 103L = 103 kg  —  m=4.105kg ( a usina utiliza essa massa de água por segundo)

Potência elétrica total recebida pela usina em 1s  —  P_t=m.g.h/Dt=4.10⁵.10.9/1  —  P_t=36.10⁶W  —  Potência útil=90 % de P_t=36.10⁶ x 0,9  —  P_u=32,4.10⁶W=32,4 MW

b) cálculo da energia elétrica útil produzida pela usina hidrelétrica em u mês=720h  —  P_u=W_u/Dt  —  32,4.10⁶=W_u/720  — 

W_u=23.328.10⁶Wh  —  regra de três  —  1 habitante – 36.10⁴Wh  —  N habitantes – 23.328.10⁶Wh  —  N=23.328.10⁶/36.10⁴  — 

N=64.800 habitantes

35- E_R = 300 kWh = 300.10³.(J/s).3600 s = 1.080.000×10³ J = 1,08×10⁹ J  —  E_C = 180×30.000 = 5. 400 .000 kJ = 5,4×10⁹ J  — 

E_C/E_R=5,4.10⁹/1,08.10⁹=5  —  R- E

36- a) No trecho em que a força de tração é constante, calculando a área do retângulo (figura), você está calculando o trabalho

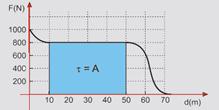
realizado  —  trabalho = área=base.altura  —  W=(50 – 10).800  —  W=32.000J

b) O trabalho realizado foi de 444.000 J no intervalo de tempo de 40 s  —  como potência é a razão entre o trabalho realizado e o intervalo de tempo  —  P_o = (Trabalho)/Dt = 444.000/40 = 11.100 W  —  em  para cavalo-vapor  —   11.100/740   —  P_o= 15 CV.

37- Dados  —  quantidade de anéis  —  n = 100  —  volume de água em cada anel  —  V = 1 cm³= 10^-6 m³  —  densidade da água  —   d = 1 g/cm³ = 10³ kg/m³  —  altura de elevação  —   h = 2 m  —  período de rotação do eixo  —   T = 2 s  —  volume total de água contido nos 100 anéis  —  V_T = n V = 100.(10^-6) m³ = 10^-4 m³  —  esse volume representa uma massa de  —  M = d V_T=

10³.(10^-4) = 10^-1 kg  —  tempo de elevação dessa massa de água  —  Dt = 100.T = 100.(2)  —    Dt = 200 s.

Potência útil da fonte de rotação  —  P_o=W/Dt=E_potencial/Dt=Mgh/Dt  —  P_o=10^-1.10.2/200=2/200=1/100  —  P_o=1,0.10^-2W  — 

R- D

38- A potência (em watt) é a razão entre a energia transformada (em joule) e o tempo (em segundo)  —  1W=1J/1s  — 4.800W=4.800J/1s  —  4.800W=4.800J/s  —  R- A

 39- a) Dados  —  n = 10 voltas  —  Dt = 20 s  —   freqüência  —  f=n/Δt=10/20  —  f=0,5Hz  —  velocidade angular  —  W=2πf=2π.0,5  —  W=π rad/s

b) Dado  —  F = P = 450 N  —  ∆S = h = 0,5 m  —  o trabalho (W) realizado pela enfermeira é igual ao trabalho para levantar o peso  —  W=P.h=450.0,5  —  W=225J

c) Calculando a potência  —  P_o=W/Δt=225/20  —  P_o=11,25W

40- Dados  —  1 cal  4J  —  1 telha = 1,5 kg  —   g = 10 m/s²

a) São dados  —  n = 20  —   m = 1,5 kg  —   g = 10 m/s² —   h = 3 m  —   v = 0,1 m/s  —   r = 20%  —   ∆t = 2 h = 7.200 s  —   1 cal = 4 J  —  como o transporte é feito com velocidade constante, a força exercida pelo trabalhador em cada levantamento tem a mesma intensidade do peso de 20 telhas  —  a potência (P) é dada pelo produto da intensidade da força (F) pelo módulo da velocidade (v) e o trabalho realizado (W) é igual ao produto da potência pelo tempo (∆t)  —  P=F.V  —  W=P_o.Δt  —  W=F.V.Δt  —  W=20mgVΔt=20.1,5.10.0,1.7200  —  W=216.000J  —  esse trabalho corresponde a 15% da energia (E) a ser ingerida  —  0,15E=216.000  —  E=216.000/0,15  —  E=1.440kJ  —  em quilocalorias  —  E=1.440/4  — E=360kcal

b) Seja N o número de telhas transportadas em 2 h  —  W = N m g h  —   N = W/mgh  —  N=216.000/1,5.10.3  —  N=4.800 telhas

41- P_o=W_F/Δt  —  P_o=W_F/Δt  —  o tempo de realização de um trabalho é inversamente proporcional à potência empregada  —  isso significa que quanto menor é o tempo, maior é a potência  —  R- B

42- A potência corresponde à  medida da rapidez com que se transfere energia  —  P_o=W/Δt  —  observe nessa expressão que o mais eficiente (maior potência) é aquele que fornece maior quantidade de energia em menos tempo  —  R- C

43- Dados  —   m = 400 kg  —   g = 10 m/s²  —   1 litro de O₂ libera 4,9 kcal  —  fazendo a conversão da energia liberada por 2,5 L de O₂  —   E_liberada = 2,5(4,9)(4.200) = 51.450 J  —  essa energia corresponde a energia potencial adquirida pelo bloco  —  E_potencial = E_liberada  —  mgh = E_liberada  —  400(10)h = 51.450  —  h ≈12,9 m. 

R- B

44- Dados  —  1 L = 1.000 mL de O₂ libera 4,9 kcal = 4,9´4.200 = 20.580 J  —  Dt = 1 min = 60 s  —  cálculo da quantidade de energia liberada (E) pela absorção de 50 mL  —  E=(50mL).(20.580J)/(1.000mL)=1.029J  —  potência liberada por kg de massa da pessoa  —  P_o=E/Δt=1.029/60  —  P_o=17,15W  —  R- D

 

45-W=F.d.cos60^o=25.20.0,5  —  W=250J  —  P=W/∆T=250/5  —  P=50W  —  R- B.

 

46-  Energia (Trabalho) necessária  para elevar uma massa m de água à altura de h=80cm=0,8m  —  W=m.g.h=m.10.0,8  —  W=8.m  —  massa de água que essa bomba de potência Po=20W consegue elevar com essa energia W=8.m em ∆t=1s  —  Po=W/∆t  —  20=8m/1  —  m=20/8=2,5kg  —  como o enunciado afirma que 1kg de água equivale ao volume de 1L  —  V=2,4L  —  R- B 

47– Po=W/∆t  —  W=Po.∆t  —  lâmpadas  —  W1=0,1.10=1kWh  —  televisão  —  W2=0,1.8=0,8kWh  —  geladeira  —  W3=0,3.24=7,2kWh  —  ventilador  —  W4=0,125.8=1,0kWh  —  Wtotal=1,0 + 0,8 + 7,2 + 1,0=10,0kWh  —  1 painel – 0,5kWh  —  n painéis – 10,0kWh  —  N=20 painéis  —  R-

48-Volume de combustível consumido em 1 hora  —  V=8L=8dm3=103cm3  —  massa de combustível consumida em 1 hora  —  d=m/V  —  0,675=m/8.103  —  m=5,4.103g  —  calor fornecido pela queima dessa massa de combustível  —  regra de três  —  1g – 10000cal  —  5,4.103g – Q cal  —   Q=5,4.107cal  —  transformando essa energia em joules  —  regra de três  —  1cal – 4J  —  5,4.107cal  —  W J  —  W=4.5,4.107=2,16.108J  —  potência gerada em 1 hora=3600s  —  P=W/∆t=2,16.108/3600  —  P=6.104W  —  a potência desenvolvida pelo carro é a potência útil=24kW=24.103W  —  rendimento=potência útil/potência total  —  η=Pu/Pt=24.103/6.104 =0,4×100=40%  —R- C 

49- a) Observe no gráfico que eles vão ter a mesma velocidade no ponto onde a reta (andando) e a curva (correndo) se interceptam que é aproximadamente de V=8,5km/h (eixo horizontal-velocidade)  — observe também no eixo vertical (volume) que a partir dessa velocidade o consumo de oxigênio do atleta que está correndo é menor do que o do atleta que está andando.

b) Do gráfico, quando ele está parado, velocidade nula eixo horizontal, o volume de oxigênio é de 0,2 ℓ/min  —  em 12h de repouso ele consumirá  —  V_r=720.0,2=144ℓ de oxigênio.

c) Pelo gráfico, quando sua velocidade é de 15km/h ele consome 3,6ℓ/min  — do enunciado, para cada litro de oxigênio consumido são gastas 5 kcal  —  energia (W) consumida quando V=15km/h  —  W=3,6.5=18kcal  —  1 cal= 4 J  —  W=18.000calx4=72.000J  — essa energia é consumida em 1min=60s  —  P=W/∆t=72kJ/60s  —  P=1,kW=1.200W.

W=72kJ.

d) O gráfico fornece que a cada 7km/h, andando, o consumo de oxigênio é de 1,6 ℓ/min  —  energia em ∆t minutos  —  W=1,6.5=8kcal  — barra de chocolate=560kcal  —  regra de três  —  1 min – 8kcal  —  ∆t min – 560kcal  —  ∆t=560/8=70 min  —  ∆t=60min.

50-a) Pelo enunciado, a potência útil  P (W) desse sistema para bombeamento de água pode ser obtida  pela expressão P = 0,1xAxv³  — 

P=0,1.2.A=2m² e v=5m/s  —  P=0,1.2.5=25W  —  P=25W.

b) O trabalho (quantidade de energia) para elevar uma massa m de água a uma altura vertical de h=7,5m é dado por W=m.g.h  —  d=m/V  —  1kg/L=1000g/1000cm³=1g/cm³  —  d=1kg/L  —  1kg/L=m/1L  —  m=1kg  —  W=1.10.7,5  —  W=75J.

c) P=W/∆t  —  25=mgh/∆t  —  25=d.V.g.h/∆t  ===  25=1.V₁.10.7,5/∆t  —  25/75=V₁/∆t  —  V₁/∆t=V₁/1=volume de água bombeado em 1s=25/75=1/3  —  V₁=(1/3) L.

d) Analisando a expressão fornecida pelo enunciado P = 0,1xAxv³ você  observa que a pressão P é diretamente proporcional ao cubo da velocidade v  —  se v for reduzida à metade a potência P ficará 2³=8 vezes menor, o que implica que a vazão (V₁=(1/3)L também ficará dividida por 8  — V₂=(1/3.8)L=(1/24) L  —  V₂=(1/24) L.

 

Voltar para os exercícios