Polias ou Roldanas – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Polias ou Roldanas
01– Observe que temos duas polias móveis — n=2 — F =25/2n — 25 = Q/22 — Q = 100N.
02– a) Uma roldana móvel, o homem deve aplicar uma força 2n=21=2 vezes menor, ou seja, de 550/2=275N.
b) Duas vezes menor, ou seja, de 0,5m.
03– O dinamômetro indica a intensidade da força que traciona o fio que está preso ao solo, ou seja, 400N. Observe na figura, que a
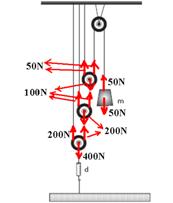
distribuição de forças nos fornece o peso do bloco, 50N. Como P=m.g — 50=m.10 — m=5kg
04– Peso do carro — PC=m.g — PC=700.10 — PC=7000N
Chamando de P o peso do contrapeso, de m sua massa, e colocando todas as forças, observamos
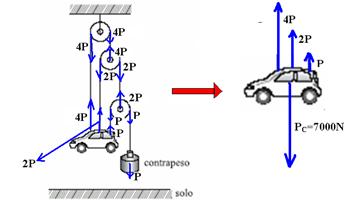
que sobre o carro agem as forças 7P (para cima) o peso do carro PC=7000N (para baixo). Como ele está em equilíbrio — 7P=PC — 7P=7000 — P=1000N e m=100kg.
O cabo central exerce uma força de 2P (veja figura) — F=2.1000 — F=2000N
05– Observe a figura abaixo:
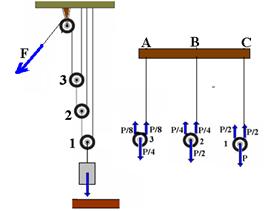
R- A
06– Três polias móveis n=3 — 2n=23=8 vezes menor
07– P=m.g — P=8.10 — P=80N — Observe nas figuras abaixo as distribuições de forças.
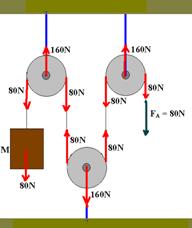
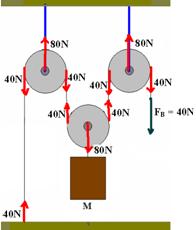
Observe também que no esquema A todas as polias são fixas e o peso do bloco é transmitido integralmente (FA=80N).
No esquema B temos uma polia móvel e o peso do bloco cai pela metade.
08– Forças que agem sobre você — seu peso de intensidade — P=m.g — P=60.10 — P=600N e a indicação da balança N

Desce acelerando — P – N = m.a — 600 – N=60.3 — -N=180 – 600 — N=420N — você se sente “mais leve” (peso aparente).
09– a) Quem está sobre a balança é a pessoa de massa 70kg e sobre ela agem duas forças. Seu peso P para baixo, que ela troca com a Terra, de intensidade P=m.g=70.10 — P=700N e a força normal N para cima, que ela troca com a balança.

Como ele sobe acelerando, a balança indicará um valor maior que o peso (N>P) — FR=m.a — N – P = m.a — N – 700=70.3
— N=700 + 210 — N=910N
b) A força de tração para cima nos cabos está puxando o elevador mais a pessoa (sistema) de peso — P=(1000 + 70).10 —
P=10.700N.

Como ele sobe acelerando T>P — FRm.a — T – 10.700 = 1.070.3 —T=10.700 + 3.210 — T= 13.910N
Como temos três cabos, a força de tração em cada cabo será 13.910/3 — T=4.636,7N
c) A pessoa bateria com a cabeça no teto e depois cairia com a mesma aceleração e velocidades que o elevador.
10– O peso aparente corresponde à força normal N — FR=ma — P – N=m.a — 100 – N =10.5 — N=50N.
11– Sobre o corpo agem duas forças. A indicação do dinamômetro para cima (T=2,5N) e o peso para baixo (P=2,0N). Sendo T>P, ele está subindo e acelerando ou descendo e freando. R- D
12– A tração máxima suportada pelo cabo vale T=m.g=1200.10 — T=12.000N.
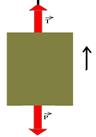
O peso do elevador é de P=1000.10 — P=10.000N. — sobe acelerando – T>P — FR=m.a — T – P =m.a — 12000 – 10.000=
1.000.a — a=2m/s2.
13– O peso da pessoa é constante e vale — P=m.g — P=80g (g é pedido) — Quando o elevador sobe com aceleração a, N=960N e
FR=ma — N – P=ma — 960 – 80g = 80a I
Quando o elevador desce com aceleração a, N=640N e FR=ma — P – N=ma — 80g – 640=80a II
Somando I com II obtemos a=2m/s2, que, substituído em I ou em II nos forneceg=10m/s2.
Então o peso da pessoa é P=mg — P=80.10 — P=800N. Quando a balança registrar 800N está registrando o peso da pessoa e nesse caso o elevador estará em repouso ou subindo ou descendo em MRU.
Quando a balança registrar zero o elevador e a pessoa estão em queda livre.
14– Os órgãos internos só se movem ou tendem a se mover, por inércia, quando houver variação de velocidade, ou seja, surgir aceleração. R- D
15– Se indica um peso maior, N>P e o elevador pode estar subindo e acelerando ou descendo e freando. R- C
16– P=m.g — P=0,8.10 — P=8,0N — tração máxima que o fio suporta — T=9,6N — FR=m.a — T – P=ma — 9,6 – 8,0=0,8.a — a=1,6/0,8 — a=2,0m/s2. Como T>P, ele sobe acelerando ou desce freando. R- C
17– Vamos colocar todas as forças que agem sobre o homem e sobre o elevador
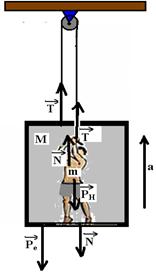
Pe – peso do elevador — Pe=Mg PH – peso do homem — PH=mg — N – força trocada entre o homem e o piso do elevador — T – força de tração na corda que puxa o homem e o elevador para cima.
Homem — FR=ma — T + N – PH=ma — T + N – mg = ma I
Elevador — FR=Ma — T – Pe – N = Ma — T – Mg – N = Ma II
Somando I com II — 2T – Mg – mg = Ma + ma — 2T = (M + m)g + (M + m)a — T=(M + m).(a + g)/2
18– a=g/5 — Desce acelerando — N<P — FR=m.a — P – N=m.a — m.g – N=m.g/5 — N=(5mg – mg)/5 — N=4mg/5 I
P=mg II — Dividindo I por II — N/P=4mg/5X1/mg — N/P=4/5 R- D
19– Sobre o elevador temos T=4f=4.1350 — T=5400N (para cima) e P=mg=600.10 — P=6000N (para baixo). — FR=ma —
P – T=m.a — 6000 – 5400=600.a — a=600/600 — a=1m/s2.
20– Considerando o sistema, elevador mais pessoa de massas (M + m) — desce freando — T>P — FR=m.a — T – P=(M + m).a — T – (M + m).g= (M + m).a — T=(M + m).(a + g) R- B
21– Colocando a força pedida e o peso que interessa:
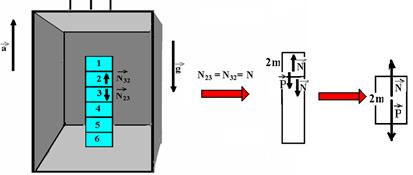
Como o bloco de massa 2m sobe freando com aceleração a, N<P — FR =m.a — P – N=2m.a — 2mg – N=2m.a —
N=2m(g – a).
22-O astronauta tem que descer com aceleração igual à da gravidade da Lua que é 20% da terrestre
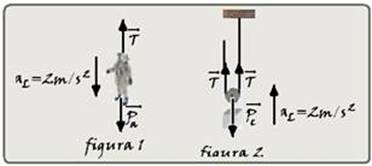
— al=0,2.10=2m/s2 — observe a figura 1 onde estão colocadas as forças que agem sobre o astronauta — FR=m.a — Pa – T = ma.aL — 220.10 – T = 220.2 —
T=2200 – 440 — T= 1760N — essa tração é transmitida até o contrapeso — figura 2 — o contrapeso deve subir com a mesma aceleração que o astronauta está descendo, ou seja, aL=2m/s2 — FR=mc.aL — 2T – Pc = mc.aL — 2.1760 = mc.10 =
Mc.2 — mc≈293kg — como, segundo o enunciado existem forças de atrito, este resultado é aproximado eestá mais próxima da alternativa A — R- A
23-Para que a distância vertical entre os centros de massa de cada um passe de 9m para 4,5m, o contrapeso deve estar verticalmente mais abaixo que o astronauta e cada um deles deve se deslocar de S=4,5/2=2,25m (veja figura) — escolhendo um
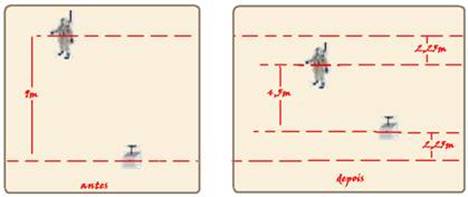
deles, por exemplo, o astronauta — ele deve subir Sa=2,25m enquanto que no mesmo tempo o contrapeso desce de 2,25m — equação do astronauta — Sa=So + Vot + a.t2/2 — 2,25 = 0 + 0.t + 2.t2/2 — t2=2,25 — t=1,5s — R- D
24–Pelo enunciado eles se movem com acelerações de 0,2gTerra, mas como existe atrito essa aceleração vai diminuir com a dissipação de energia — R- B
