Plano inclinado sem atrito – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Plano inclinado sem atrito

 

01-

a)

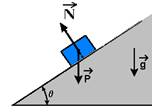
b)

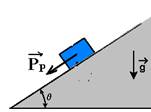
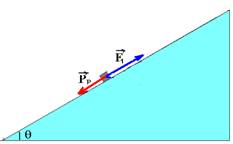
F_R=P_P=Psenq =mgsenq  —   direção paralela ao plano, no sentido para baixo (oposto ao do lançamento) que retarda o bloco na subida e o acelera na descida.

02- R- C  —  veja a teoria

03- Forças que agem sobre o balcão na direção do movimento:

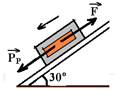
P_P  —  parcela do peso que tenta fazer o bloco descer o plano inclinado  —  P_P=m.g.sen30^o  —  P_P=200.10.0,5  —  P_P=1.000N

F  — intensidade da força aplicada pelo empregado sobre o balcão fazendo-o descer com velocidade constante, ou seja, está em equilíbrio estático (F_R=0). Assim, F=P_P=1.000N_.

04- P_P=m.g.senq  —  P_P=5.10.0,8  —  P_P=40N

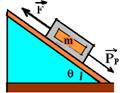
Como ele sobe com aceleração de 3m/s², F_R=m.a  —  F – P_P=m.a  —  F – 40=5.3  — F=55N R- D

05- A força que reduz a velocidade do bloco é P_P=m.g.senq  —  P_P=F_R=m.a  —  m.g.senq= m.a  —  a=g.senq

Como ele pára em C – V=0  —  Torricelli  —  V² = V_o² + 2.a.DS  —  0² = V_o² + 2.(-g.senq).BC  —  BC = V_o²/2.g.senq

06- Cálculo da aceleração de subida e de descida do carrinho  —  P_P=F_R=m.a  —  m.g.sen30^o = m.a  —  a=g.sen30^o  —

a=10.0,5  —  a=5m/s²

1^a etapa  —  tempo de subida com a velocidade variando de V_o=10m/s a V=0 e com a=-5m/s²

—  V=V_o + a.t  —  0=10 – 5t  — t=2s (tempo de subida) 

 

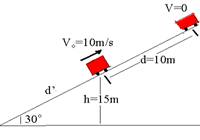
—  distância percorrida na subida  —  d=V_o.t + a.t²/2  —  d=10.2 – 5.2²/2  —  d=10m 

2^a etapa  —  cálculo de d’  —  sen30^o=15/d’  —  d’=15/0,5  —  d’=30m  —  tempo que o carrinho demora para ir do topo do plano inclinado (V_o=0) até sua base, percorrendoDS=40m com a=5m/s².

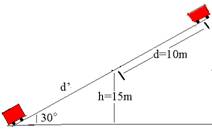
DS= v^o.t + a.t²/2  —  40=0.t + 5.t²/2  —  t²=16  —  t=4s  —  tempo total de subida e descida = 2 + 4=6s

07- A parcela do peso paralela ao plano inclinado vale  —  P_P=mgsenq. A parcela de F (F_P), paralela ao plano inclinado vale:

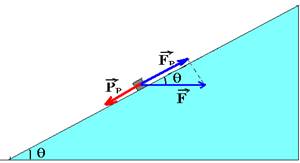
cosq=cateto adjacente/hipotenusa  —  cosq=F_P/F  —  F_P=F.cosq  —  sendo F=P=mg  —  F_P=mgcosq

Como o bloco sobe com aceleração a  —  F_R=m.a  —  F_P – P_P=m.a  —  mgcosq – mgsenq=m.a  gcosq – gsenq =a  —  10.0,8 – 10.0,6=a  —  a=2m/s².

08- Forças que agem sobre o corpo na figura 1 

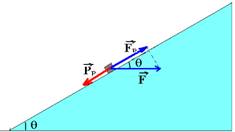
Como o corpo está em repouso  —  F_R=0  — P_P=F_P  —  P.sen30^o = F.cos30^o  —  P/2 = F.Ö3/2  —  P=F.Ö3 I 

Forças que agem sobre o corpo na figura 2

Como o corpo está em repouso  —  F_R=0  —  P_P=F₁  —  P.sen30^o = F₁  —  P/2=F₁  — P=2F₁ II

Igualando I com II  —  F.Ö3 = 2.F₁  —  F₁/F=Ö3/2

09- Em A  —  N=P  —  N=100N (indicação da balança)

Em B  —  N=P_N  —  N=P.cosa  —  N=100.cateto adjacente/hipotenusa  —  N=100.40/50  —  N=100.0,8  —  N=80N  R- D

10- Da figura 2  —  V_o=6m/s  —  V=0  — t=1,2s  —  V=V_o + a.t  —0=6 + a.1,2  —  a= – 5m/s²  em módulo a=5m/s²

A força que retarda o bloco é P_P tal que  —  F_R=m.a  —  P_P=m.a  —m.g.sena=ma  —  10.sena=5  —  sena=1/2  —  a=30^o

Em todo gráfico VXt o deslocamento do corpo é fornecido pela área  —  de 0 a 0,4s a área é:

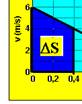
DS=área do trapézio=(B + b).h/2  —  DS=(6 + 4).0,4/2  —  DS=2m.

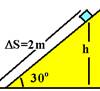
sen30^o=h/2  —  0,5=h/2  —  h=1m   R- B

11- a) Como não tem atrito  —  F_R=P_P=m.g.sen37^o=1.10.0,6  —  F_R=P_P=6N

b) F_R=m.a  —  6=1.a  —  a=6m/s²  —  DS=V_o.t + a.t²/2  —  12=0.t + 6.t²/2  —  t=Ö4  —  t=2s

12– Colocando as forças:

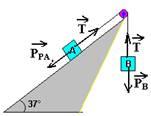
Bloco A  —  sobe com aceleração de 2m/s² tal que  —  T – P_PA=m_A.a  —  T – m.g.sen37^o=1.2  —  T=1.10.0,6+2  —  T=8N

Bloco B  —  desce com a=2m/s²  —  P_B – T=m_B.a  —  m_B.10 – 8=m_B.2  — 8m_B=8  —  m_B=1kg  —  P_B=10N  R-D

13– Colocando as forças:

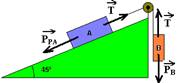
 Repouso  —  F_R=0  —  bloco B  —    P_B=T  —  T=m_B.g  —  T=8.10  —  T=80N     bloco A  —  P_PA=T  — P_A.sen45^o=80  —

P_A.Ö2/2=80  —  P_A=80.Ö2N

14- a)Figura 1: M₂  —  P=10.10  —  P=100N  —  M₁  —  P_P=m.g.sen30^o  —  P_P=10.10.1/2  —  P_P=50N

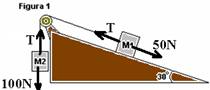
O sistema se move no sentido anti-horário  —  100 – T=10.a I  —  T – 50=10.a II  —  somando I com II  —  50 =20.a  —  a=2,5m/s² e é a mesma para os dois blocos.

b) figura 2  —  observe que a polia de baixo é móvel, então ela transmite apenas metade do peso de M₂ para M₁ sendo que a outra metade é suportada pelo teto em A.

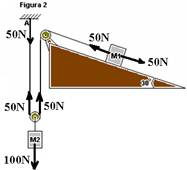
Assim, observe que a força resultante sobre M₁ é nula e a=0.  O mesmo ocorre com M₂.

15-   m  —  P=10m  —  M  —  observe na figura abaixo que q e a são complementares portanto sena=cosq  —    P_P=mgsena=mgcosq  —  P_P=8.10.Ö3/2  —  P_P=40Ö3N

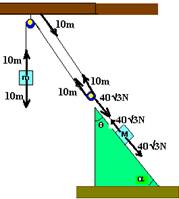
Observe na figura acima que do peso de M apenas 10m é transmitido a m, pois os outros 10m são sustentados pelo teto. Assim,

10m=40Ö3  —  m=4Ö3kg.  R- B

16- Como não existe atrito o sistema se move no sentido horário. Colocando as forças que atuam na direção do movimento.

P_PB=m_B.g.sen30^o=3.10.0,5  —  P_PB=15N

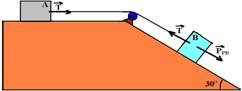
bloco A  —  F_R=m_A.a  —  T=2.a I  —  bloco B  —  F_R=m_B.a  —  P_PB – T=3.a   —   15 – T=3.a II  —  somando I com II  — 

15=5.a  —  a=3m/s²  —  T=2.3  —  T=6N.

a.

17- Dados: m₁= 0,4 kg; m₂= 0,6 kg  —  Analisando a figura:

 

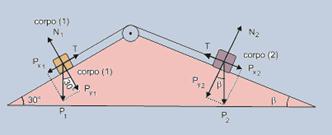
Como os corpos estão em equilíbrio, as forças também se equilibram em todas as direções: Assim:

T = P_x1 T = P_x2  —  P_x2=P_x1  —  m₂gsenβ=m₁gsen30^o  —  senβ=m₁/m₂.sen30^o  —  senβ=1/3  —  β=arc sem 1/3

18- Como os atritos são desprezados, o movimento é acelerado no plano inclinado e uniforme no plano horizontal: 

 

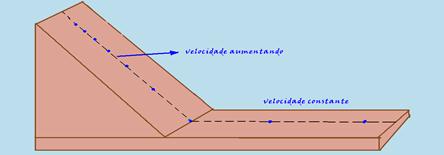
R- B

19- Como não existe atrito, a força resultante sobre o bloco na direção do deslocamento, tem intensidade  —  F_R=P_p=mgsen30^o  —  pela lei fundamental da dinâmica F_R=ma  —  mgsen30^o=ma  —  a=gsen30^o=10.1/2  —  a=5m/s²  —  S=S_o + V_ot + at²/2  —  4=0 +

0.t + 5t²/2  —  t²=1,6  —  t≈1,26s
20- A intensidade da força resultante sobre o bloco na direção do movimento é F_R=P_p=mgsenθ=ma  —  a=gsenθ  —  quando t=1s – S=d  —  d=at²/2  —  d=gsenθ.1²/2  —  d=gsenθ/2  —  quando t=3s  —  d’=at²/2  —  d’=gsenθ.9/2  —  d’/d=(9.gsenθ/2)/gsenθ/2  —  d’=9d  —  R- C

21- a) mgsen30^o=ma  —  a=gsen30^o=10.1/2  —  a=5m/s²  —  falsa

b) cálculo do deslocamento ΔS  —  equação de Torricelli  —  V²=V_o² + 2.a. ΔS  —  6²=0²+ 2.5.ΔS  —  ΔS=3,6m  —  altura h  —  sen30^o=h/3,6  —  h=1,8m  —  correta

c) V=V_o + at  —  6=0 + 5t  —  t=1,2s  —  correta

d) Na base  —  I=m.ΔV=2.(6 – 0)  —  I=12N.s  —  correta

e) Trabalho na vertical  —  W=P.h=20.1,8  —  W=36J  —  correta

R- (F,C,C,C,C)

22- Os corpos se movimentam nos seguintes planos inclinados:

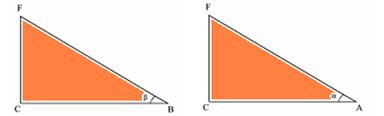
As componentes dos pesos de P₁ e P₂, ao longo das respectivas trajetórias, são dadas por  —  F₁=Psenβ  —  F₂=Psenα  — 

F₁/F₂=senβ/senα  —  senβ=CF/BF=6/10  —  AF é a diagonal do paralelepípedo  —  (AF)²=36 + 64 + 225  —  AF=5√13  –senα=CF/AF=6/5√13  —  F₁/F₂=6/10 x 5√13/6  —  F₁/F₂=√13/2  —  R- E

 

23-

Observe que os dois triângulos são pitagóricos, então a altura de I vale 4m e a de II, 3m  —  como não existe atrito

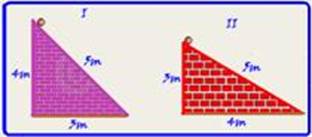
e a força peso é conservativa (independe da trajetória), você pode considerá-las como em queda livre, com a=g e V_o=0, I da altura de 4m e II da altura de 3m  —  Torricelli  —  I  —  V_I² = V_oI² + 2gh_I=0² + 2.10.4  —  V_I = √80  — 

II  —  V_II² = V_oII² + 2gh_II=0² + 2.10.3  —  V_I = √60  —  V_II/V_I = √80/√60= (√3.√5)/(2.√5)  —  V_II/V_I=√3/2  — 

R- B.

24-

A parcela do peso responsável pela descida do bloco A é dada por P_pA=P_Asenα=m_A.g.senα  —  a figura mostra todas as forças

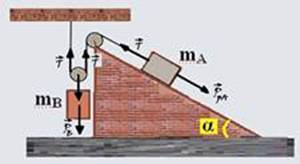
 que agem sobre o bloco  —  como o sistema está em equilíbrio a força resultante sobre cada bloco é nula  —  bloco A  —  P_pA=T  —  m_A.g.senα =T  —  bloco B  —  P_B=2T  —  m_B.g =2.m_A.g.senα  —  m_B=2m_A.g.senα  —  R- D

Voltar para os exercícios