Plano inclinado com atrito – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Plano inclinado com atrito

 

01-O plano inclinado possui uma secção transversal que é um triângulo retângulo de hipotenusa 50 cm e cateto 30 cm. O outro cateto, por Pitágoras, deve ser de 40 cm.

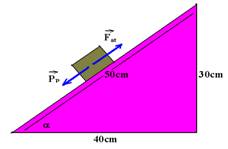
senα=cateto oposto/hipotenusa=30/50  —  senα=0,6  —     cosα=cateto adjacente/hipotenusa=40/50  —  cosa=0,8

Como o bloco está em equilíbrio a força resultante sobre ele é nula e assim, PP=Fat  —  mgsenα=μmgcosα  —  0,6=μ.0,8  —  μ=0,75

02- Como ele está com velocidade constante a força resultante sobre ele é nula e, nesse caso Fat=PP. Seja M a massa total (caminhão + combustível)  —  μMgcosα=Mgsenα  —  μ=sena/cosa=tga  —  R- D

03- A menor força de atrito para mantê-lo em equilíbrio vale F_at=P_P=Psen30^o=700.0,5  —  F_at=350N  R-A

04- Esquema:

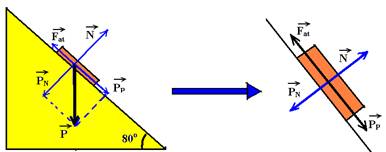
P_P=Psen80^o=P.0,98 —  no equilíbrio – F_at=P_P  —  F_at=P.0,98  —  F_at/P=0,98  —  0,98=98/100  —  98%  R-E

05- Colocando as forças na direção do movimento.

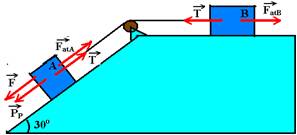
P_P=P_Asen30^o=200.0,5  —  P_P=100N  —  F_atA=μP_Acos30^o=0,25.200.0,87  — F_atA=43,5N  —  F_atB=μN=mP_B=0,25.400  —  F_atB=100N

Na iminência de movimento a intensidade da força resultante sobre cada bloco é nula  —  bloco B – T=F_atB  —  T=100N  —  bloco A –  F + P_P=F_atA + T  —  F + 100=43,5 + 100  —  F=43,5N

06- a) A reação do plano inclinado é N=P_N=Pcosθ=mgcosθ=1.10.0,8  —  P_N=8N

b) A velocidade inicial é nula (partiu do repouso) e a final também (parou). Assim, ∆V=0

c) No plano inclinado AB  —  F_at=mN_i  —  F_ati=μP_N=0,2.8  —  F_at=1,6N

No plano horizontal BC  —  F_at=μN_h=mP=0,2.10  —  F_at=2N

d) No plano horizontal a força resultante sobre ele é a força de atrito horizontal que o obriga a parar em C, ou seja, F_R=F_at

F_R=ma=F_at  —  F_at=ma  —  2=1a  —  a=2m/s²

e) Ele parte do repouso em A, desce acelerando e atinge a velocidade máxima em B (V­_B)

Torricelli  —  V_C²=V_B² + 2.a.DS  —  0²=V_B² + 2.(-2).4  —  V_B=4m/s

f) Colocando as forças que agem sobre o corpo, na direção do movimento, em sua descida pelo plano inclinado

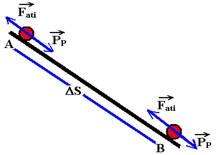
F_at=1,6N  —  P_P=Psenθ=10.0,6  —  P_P=6N  —  F_R=ma  —  P_P – F_ati=ma  —  6 – 1,6=1.a  —  a=4,4m/s²

Torricelli  —  V_B²=V_A² + 2.a.∆S  —  4²=0² + 2.4,4.∆S  —  ∆S»1,8m

07- a) Como no plano inclinado não existe atrito a força resultante sobre o corpo é o P_P  —  F_R= P_P=ma  —  μgsen30^o=ma  —  10.10.0,5=10.a  —  a=5m/s²  —  ∆S=V_o.t + a.t²/2  —  ∆S=0.2 + 5.2²/2  — ∆S=10m

b) Cálculo da velocidade V_p com que o corpo chega à base do plano inclinado  —  V_p=V_o + at  —  V_p=0 + 5.2  —  V_p=10m/s

No plano horizontal existe atrito e a força resultante é o próprio F_at 

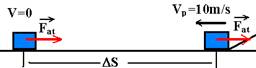
F_R=F_at=m.a  —  μN=m.a  —  μP=ma  —  0,2.100=10.a  —  a=2m/s²

Torricelli  —  V² = V_p² + 2.a.∆S  —  0² = 10² + 2.(-2).∆S  —  ∆S=25m

08– Forças que agem sobre o bloco na direção do movimento:

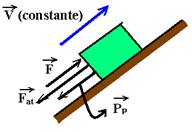
F_at=μmgcosa=0,5.4.10.0,8  —  F_at=16N  —  P_P=mgsena=4.10.0,6  —  P_P=24N  —  no equilíbrio dinâmico  —  F_R=0  — F=P_P + F_at  —  F=24 + 16  —  F=40N

R- E

09- Como g é o mesmo (mesmo focal), se P_B=10P_A  —  m_B=10m_A.

Colocando as forças

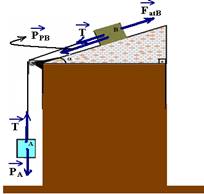
Como está com velocidade constante está em equilíbrio dinâmico e a força resultante sobre cada bloco é nula  —  bloco A  —  T=P_A  —  T=m_Ag   —  bloco B  —  F_atB=P_PB + T  —  μm_Bgcosα = m_Bgsenα + m_Ag  — μ10m_Agcosα =10m_Agsenα + m_Ag  —  μ.10.0,8=10.0,6 + 1  —  8μ=1,6  —  μ=0,875

R- C 

10- Colocando as forças:

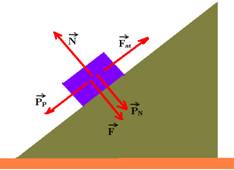
senα=0,6/1  —  senα=0,6  —  cosα=0,8/1  —  cosα=0,8  —  como ele está em repouso a força resultante sobre ele é nula, então  —   P_P=F_at  —  mgsenα = μN  —  mgsenα =μ(P_N + F)  —  mgsenα = μ(mgcosa + F)  —  2.9,8.0,6 = 0,4.(2.9,8.0,8 + F)  —  11,76 = 6,272 + 0,4F  —  F=5,488/0,4  —  F=13,72N  R- A

11- P_P e F_at são os mesmos tanto na figura 1 como na figura 2

a) figura 1  —  P_P=mgsen30^o=5.10.0,5  —  P_P=25N  —  comparando V=V_o + a.t com V=2,0.t, concluímos que V_o=0 e a=2m/s²

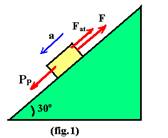
F_R=ma  —  P_P – F –F_at=ma  —  25 – F – F_at=5.2  —  F + F_at=15 I 

Figura 2  —  P_P=25N  —  comparando V=V_o + a’.t com V=3,0.t, concluímos que V_o=0 e a’=3m/s² 

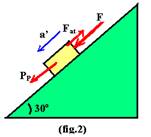
F_R=ma’  —  P_P + F – F_at=ma’  —  25 + F – F_at=5.3  —  F=F_at – 10 II  —  II em I  —  F_at– 10 + F_at=15  —  F_at=12,5N  —  F + F_at=15  —  F + 12,5 = 15  —  F=2,5N

b) F_at=μmgcos30^o  —  12,5=μ.5.10.√3/2  —  μ=12,5/25√3  —  μ»0,3

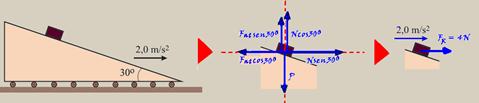
12- a)Cálculo da aceleração pelo gráfico  —  a=∆V/∆t=2,0/1,0  —  a=2m/s²

b) F_R=ma —  P_P – F_at=ma  —  mgse30^o – F_at = m.a  —  0,2.10.0,5 – F_at=0,2.2  — F_at=0,6N

13-  I- Correta, pois P_PB é sempre menor que P_A.      II- Falsa, vide I.      III- Não necessariamente, pois F_atB de dos valores do coeficiente de atrito m e do ângulo de inclinação do plano.      IV- Correta, vide I.   R- D

14-

a)

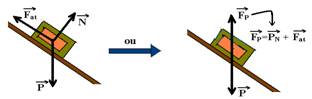
b) Na direção do plano de apoio as forças que agem sobre a caixa são:

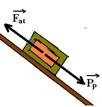
Como a caixa está em repouso, a força resultante sobre ela é nula  —  

c) P_P=F_at  —  mgsen30^o=μmgcos30^o  —  0,5=μ0,87  —  μ»0,57

15- Cálculo da aceleração  —  Torricelli  —  V_B²=V_A² + 2.a.∆S  —  9=4 +2.a.1  — a=2,5m/s²  —  F_R=ma  —  P_P – F_at=m.a  — mgsen60^o – μmgcos60^o=m.a  —  10.√3/2 – m.10.0,5=2,5  —  5√3 – 5m=2,5  —  m=√3 – 1/2   R- E

16- As forças que agem sobre a telha são P_P e F_at:

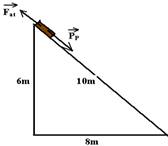
Se a hipotenusa é 10 e um cateto é 6, aplicando Pitágoras, o outro cateto é 8  —  senα=6/10=0,6  —  cosα=8/10=0,8  —  F_R=ma  —  P_P – F_at=ma  —  mgsena – μmgcosa=ma  —  10.0,6 – 0.2.10.0,8=a  —  a=4,4m/s²

17- Colocando as forças:

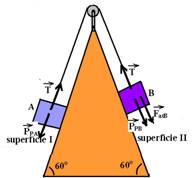
Como o bloco A está descendo, B está subindo e o F_at nele é para baixo  —  bloco A – não tem atrito  – F_R=ma  —  P_PA – T=ma  —  mgsen60^o – T=ma  —  √3/2mg – T=ma I  —  bloco B – tem atrito  —  T – P_PB – F_atB=ma  —  T – mgsen60^o – μmgcos60^o=ma  —  T – mg√3/2 – 0,2.m.g.0,5=ma II  —  somando membro a membro I com II   —  -0,1m=2ma  —  a=-0,5m/s²  —  V=Vo +a.t  —  V=3 – 0,5.2  —  V=2m/s

 

18-Colocando as forças

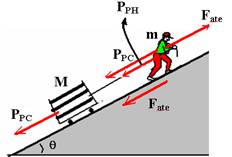
Sobre o homem agem as forças  —  F_ate=μN  —  F_ate=μP_N  —  F_ate=μmgcosq  – força de atrito estático máximo que ele troca com o plano inclinado e que é responsável por ele subir sem escorregar  —  P_PC=Mgsenθ – força com que ele puxa o carrinho de massa M através do fio —  P_PH=mgsenqθ  —  parcela de seu peso de massa m, que ele deve vencer F_ate=P_Pc + P_PH  —  μmgcosθ=Mgcosθ + mgsenθ  —  M=m(mcosq – senq)/senq  —  M=m(mcosq/senq – senq/senq)  — 

M=μ(mcosθ/senθ – 1) R- E

19-Cálculo da velocidade com que o corpo chega ao ponto Q. No trecho PQ as forças que agem sobre o corpo na subida são P_P e F_at.

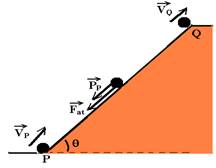
P_P=mgsenθ=m.10.0,8  —  P_P=8m  —  F_at=μmgcosθ=1/3.m.10.0,6  —  F_at=2m  —  F_R=ma  —  P_P + F_at=ma  —  8m + 2m=ma  —  a=10m/s²  —  cálculo da velocidade com que chega em Q  —  Torricelli  —  V_Q² = V_P² + 2.a.∆S  —  V_Q²=25 + 2.(-10).0,8  —  V_Q=3m/s  —  cálculo do tempo que demora para chegar em Q  —  V_Q=V_P + a.t  —  3=5 + (-10).t  —  t=0,2s

A partir de Q, aonde chega com velocidade de 3m/s, ocorre um lançamento oblíquo com ângulo de lançamento q.

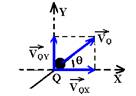
Como o exercício quer o instante em que a componente vertical da velocidade se anula, vamos trabalhar apenas com ela (eixo Y).

Decompondo V_Q no eixo vertical Y  —  V_QY=V_Qsenθ   —  V_QY=3.0,68  —  V_QY=2,4m/s   —  quando a componente vertical da velocidade se anula, V_Y=0  —  V_Y=V_o + g.t  —  0=2,4 + (-10).t  —  t=0,24s  —  t_t=0,2 + 0,24  —  t_t=0,44s

20-a) As forças que agem sobre a caixa são:

 

 

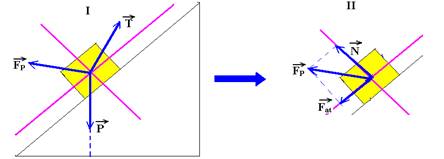
figura I  —  – peso, vertical e para baixo exercida pela Terra  —   – força de tração, exercida pelo fio  —   – força exercida pelo plano.

Figura II – a força exercida pelo plano  é a soma vetorial da força normal com a força de atrito , ou seja,  =  + .

 

b) Decompondo as forças nos eixos X e Y

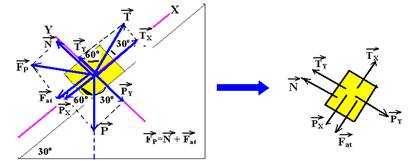
T_X=Tcos30^o  —  T_X=T√3/2  —  T_Y=Tsen30^o  —  T_Y=T/2  —  P_X=mgsen30^o  — P_X=mg/2  —  P_Y=mgcos30^o  —  P_Y=mg√3/2 F_at=μN

Equilíbrio na direção X  —  T_X=P_X + F_at  —  T√3/2=mg/2 + μN  I    —-    equilíbrio na direção Y  —  N + T_Y=P_Y  —  N=mg√3/2 – T/2 II  —  II em I  —  T√3/2=mg/2 + m(mg√3/2 – T/2)  —  T(√3 +m)=mg(1 + m√3)  —  T= mg(1 + m√3)/ (√3 + m) 

Substituindo os valores  —  T»14N

21- (a) Com rodas não existe atrito e a força resultante sobre o carrinho é P_P=F_R  —  mgsena=ma  —  a=gsena

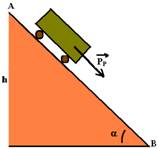
∆S=V_o.t + a.t²/2  —  ∆S=V₀.t + gsenα.t²/2 I  —  senα=h/∆S  —  ∆S=h/senα II  —  II em I  —  h/senα=gsenαt²/2  —  t²=h/senαX2/gsena  —  t²=2h/g(senα)²   —  t=(√2h/g)/senα

b) Sem rodas, existe força de atrito de intensidade  (F_at). Temo de descida agora é t₁=2t  —  t₁=2(√2h/g)/senα

∆S=V_o.t + a.t²/2  —  h/senα=0.t + a.t₁²/2  —  h/senα=a.4.(2h/g)/(senα)²  —  a=2h.(senα)².g/4senα.2h  —  a=g.sena/4 II

F_R=m.a  —  P_P – F_at=m.a  —  mgsenα – μmgcosα=m.g(senα)/4  —  senα – mcosα=(senα)/4  —  mcosα=senα – (senα)/4  — mcosα=(3senα)/4  —  m=3senα/4cosα  —  m=(3tgα)/4

 

22- A força de atrito que atua sobre o corpo é F_at = μ.m.g.cosμ = 8m.μ  —   força resultante na direção do movimento  —  F_R= m.g.sen β – 8m.μ = m.a  —  6m – 8m.μ = m.a  —   6 – 8μ. = a  —  a função horária do movimento é S = S0 + v0.t + a.t²/2  —  S_o = 0 e v_o = 0  —  S = a.t²/2  —  para t = 1 s  —   S = 1 m  —   1 = a.1²/2  —  a = 2 m/s²  —  então: 6 – 8m. = a  —  6 – 8m. = 2  — 8m. = 6 – 2  —   8m. = 4  —   m = 0,5  —  para t = 1 + 3 = 4 s  —  S = x₂  —   x₂ = 2. 4²/2  —  x₂=16m

R- D

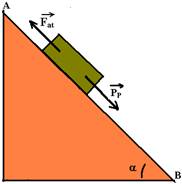
23- Observe ao figura abaixo onde estão colocadas todas as forças que agem sobre o bloco  —   P_t  = P sen 45° = m g sen 45°  —

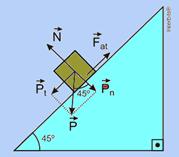
–  F_R=ma  —   N = P_n = P cos 45° = m g cos 45°  —  g  = 10 m/s²  —  a = 5 m/s²  —   θ = 45°  —   princípio fundamental da dinâmica  —  F_R=ma  —  P_t  – F_at = m a  —  mgsen45^o=μmgcos45^o=ma  —  10√2/2 – μ.10.√2/2=5  —  m = (5√2 – 5)/5√2= (√2 – 1)/√2=(1,4 – 1)/1,4  —  μ≈0,3  —  R- C

24- O corpo está em equilíbrio dinâmico (F_R=0)  —  F_at=P_p=Psenθ  —  senθ=FC/FB=6/10=0,6  —  F_at=mgsenθ=20.10.0,6  —  F_at=120N  —  R- C

25- Na iminência de escorregar, ele está em equilíbrio e, nessas condições a parcela do peso (P_p=Psenβ) que tenta desloca-lo é equilibrada pela força de atrito (F_at)  —  mgsenβ=μmgcosβ  —  μ=senβ/cosβ  —  μ=tgβ=0,40  —  tgβ=cat. oposto/cat. adjacente  —  0,40=10/x  —  x=10/0,4  —  x=25cm  —  R- A

26- Colocando as forças que agem sobre o bloco  —  decompondo-as na vertical e na horizontal  —  na vertical a força

resultante é nula  — P=F_atsen30^o + Ncos30^o  —  20=F_at/2 + N√3/2 (I)  —  na horizontal existe uma força resultante para a direita onde o bloco se move com aceleração a=2m/s² e de intensidade  —  F_R=ma  —  F_R=2.2  —  F_R=4N  —  F_R=N/2 – F_at.√3/2  —

4=N/2 – F_at.√3/2 (II)  —  resolvendo o sistema composto por I e II e substituindo √3 por 1,7, você obterá  —  F_at=6,6N   

27- Na figura estão colocadas as forças que agem sobre cada bloco  —  cálculo da aceleração do sistema considerando os dois corpos como um único de massa (m₁ + m₂)=4kg  — 

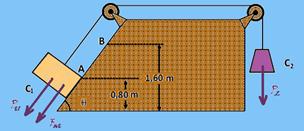
28- Trecho CD  —  F_at=μN=μP=μmg  —  F_at=10μm  —  a intensidade da força resultante é a própria força de atrito  —  F_R=ma  —  10μm=ma  —  a=10μ  —  Torricelli  —  V²=V_o² + 2.a.ΔS  —  0=V_o² + 2.(-a).20  —  V_o²=2.10μ.20  —  V_o²=400μ  —   trecho AC, sem atrito, desce com aceleração a’, sujeito à P_p=mgsenθ=m.10.12/AC=120m/AC  —  P_p=F_R=ma’  —  120m/AC=ma’  —  a’=120/AC  —  Torricelli  —  V²=V_o² + 2.a.ΔS  —  V_o²=0² + 2.a’.AC  —  400μ=2.120/AC.AC  —  μ=240/400  —  μ=0,6  —  R- E

 

29-

As forças que agem sobre o bloco na direção do movimento são  —  P_p (parcela do peso responsável pela descida

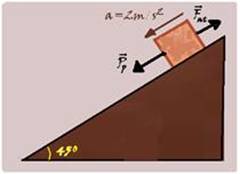
do bloco)  —  P_p=Psen45^o=mgsen45=m.10.√2/2=m.10.1,4/2=7m  —  F_at (força de atrito, sempre contrária ao movimento)  —  F_at=μ.P.sen45⁰=μ.m.g.√2/2=μ.m.10.1,4/2=7μm  —  F_R=m.a  —  P_p – F_at=m.a  —  7m – 7μm=m.2  —  μ=5/7≈0,714  —R- A.

30-

Durante a descida a intensidade da força resultante que age sobre o bloco é igual à intensidade da força de atrito

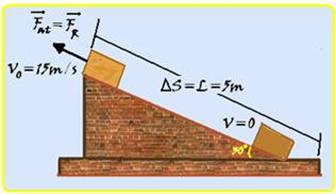
F_at=F_R —  V_o=15m/s  —  ∆S=L=5m  —  para (V=0)  —  cálculo do módulo da aceleração a pela equação de Torricelli  —  V²=V_o² + 2.(-a).∆S  —  0² = (15)² – 2.a.5  —  a=22510  —  a=22,5ms²  —  lei fundamental da dinâmica  —  F_R=m.a=4.22,5  —  F_R=90N.

31-

Trata-se de um plano inclinado onde o peso do corpo, vertical e para baixo, é decomposto em duas parcelas  —   – parcela do peso, no plano inclinado, paralela ao plano e para baixo, responsável pela descida ou tentativa de descida do bloco, de intensidade  —

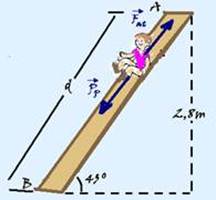
de intensidade  —  P_P=P.senα ou P_P=mgsen α—   a energia é dissipada pela força de atrito   que é sempre contrária ao movimento ou à sua tendência, de intensidade  —  F_at=μPcos45^o ou  F_at=μmgcos45^o=0,5.20.10.√2/2  —  F_at=50√2N  —  a força resultante, responsável pela descida do menino tem intensidade  —  F_R=P_p – F_at=100√2 – 50√2=50√2N  —  distância d percorrida pelo menino ao se deslocar de A para B  —  sen45^o=2,8/d  —  √2/2=2,8/d  —  d=2,8√2m  —  a energia dissipada na descida de A para B corresponde ao trabalho da força de atrito nesse trecho  —  W_Fat=F_at.d.cos180^o (180^o é o ângulo entre o F_at e o deslocamento)  —  W_Fat=50.√2.2.8.√2.(-1)  —  W_Fat= – 280J (o sinal negativo significa que essa energia foi dissipada)  —  ingestão de um sorvete  —  W_sorvete=112.00J   —  número de vezes que a criança deverá escorregar  —  n=112.000/280=400 vezes  —  R- D  

 

Voltar para os Exercícios