Pêndulo Simples – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Pêndulo Simples
01-
(01) Falsa — 20 vezes — 10s 20T = 10 — T = 10/20 — T = 1/2 s
1 vez — T
(02) Falsa — f = 1/T — f =1/1/2 — f = 2 Hz
(04) Verdadeira — T = 2pÖL/g — Observe que T é diretamente proporcional à raiz quadrada de L.
(08) Falsa — Observe na equação T = 2pÖL/g que o período T independe da massa m
(16) Falsa — Observe que o período T é inversamente proporcional à raiz quadrada de g e consequentemente diretamente proporcional à freqüência, pois f = 1/T.
(32) Verdadeira — Observe na equação T = 2pÖL/g que o período T independe da amplitude A
Soma – (04 +32) = 36
2-
a) 20 vezes — 30s 20T=30 — T = 1,5s f=1/T — f=1/1,5 — f = 0,67Hz
1 vez — T
b) Observando-se que em t = 0, x = + A, temos o gráfico senoidal a seguir.
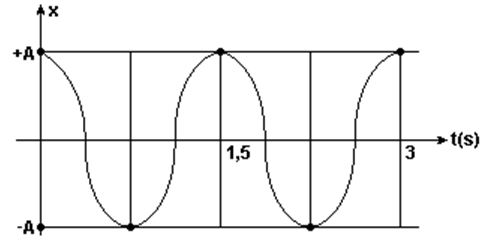
3-
(01) Verdadeira — T = 2pÖL/g — T = 2pÖ2,5/10 — T = 2p.0,5 — T = p s
(02) Falsa — ponto mais alto – h=1m — Ep=mgh — Ep=30.10.1 — Ep=300J
04) Falsa — A energia mecânica é constante e vale 300J (vide 2). No ponto mais baixo — Em = Ec + Ep —
300= mV2/2 + mgh — 300 = 30V2/2 + 30.10.0,5 — V = Ö150/15 — V = Ö10 m/s
(08) Falsa. Num pêndulo simples o período T de oscilação independe da massa m.
(16) Falsa . O período independe da altura (amplitude A).
Soma ( ) 01 + 04 = 05
4-
a) Como o comprimento do pêndulo aumenta, pois ele se dilata devido à elevação da temperatura e como raiz quadrada de L é diretamente proporcional à T, o período aumentará e o relógio atrasará.
b) Sendo T inversamente proporcional a Ög e como g diminui (gLua < gTerra), o período aumentará e o relógio atrasará
5-
O V, pois sendo T diretamente proporcional a ÖL (L=comprimento do fio), para T cair pela metade (de 2s para 1s), L deverá ser 4 vezes menor (100/4=25)
6-
a)
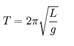
T = 2pÖ67/10 — T =2pÖ67/Ö10 — T = 2p8/p — T =16s
b) Permaneceria o mesmo, pois o período do pêndulo simples não depende da massa pendular.
7-
R: Comprimento L — T=2s
Comprimento L/4 — T’=2pÖL/4 / Ög — T’=2pÖL/g.1/2 — T’=T/2 — T’=2/2 — T’=1s
Observe na figura abaixo que o período (tempo que demora para ir e voltar) entre A e B é T/2=2/2=1s e que o período entre B e C é T’/2=1/2=0,5s
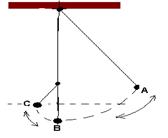
Assim, L demora 0,5s para ir de A até B; L/4 demora 0,25s para ir de B a C; L/4 demora 0,25s para ir de C a B e L demora 0,5s para ir de B a A.
Portanto o período pedido é 1 + 0,5 = 1,5s
8-: C
9-
Sendo f = 1/T — T3 > T2 > T1 — como o local é o mesmo, g é a mesma e como T é diretamente proporcional a ÖL —
L3 > L2 > L1 R: D
10- E
11-
a) T=2pÖL/g — 0,8= 2pÖL/g — (0,8)2 = 4.p2.L/g — 0,64=4g.L/g — L=0,16m=16cm — h=16 + 5 = 21 cm
b) ) T=2pÖL/g — 5= 2pÖL/g — (5)2 = 4.p2.L/g — 25=4g.L/g — L=6,25m — h=6,25 + 0,25 = 6,5m
Sim, o relógio teria de ter mais que 6,5 m
12-
6T1 = 4T2 — 6. 2pÖL1/g = 4. 2pÖL2/g — ÖL2/L1 = 6/4 — (ÖL2/L1)2 = 36 / 16 — L2 / L1 = 9 / 4
13-
T=2pÖ10/10 — T=2ps — p@3 — T@6s
86 batidas —- 60s
X batidas —– 6s
X @ 9 batidas
14- Cálculo do período T de cada oscilação — w=2π/T — T=2π/w=2π/5π/2 — T=0,8s — tempo (∆t) gasto em n=3.600 oscilações — ∆t=nT=3.600×0,8 — ∆t=2.880/60 min — ∆t=48 min — R- C
15- Período de oscilação (T) de um pêndulo simples de comprimento L em um local onde o campo gravitacional tem intensidade g, para oscilações de pequenas amplitudes — T=2π√L/g — observando essa expressão você conclui que, quando a intensidade do campo gravitacional diminui o período aumenta, ou seja, o pêndulo passa a oscilar mais vagarosamente — na ausência total de gravidade, o pêndulo teria período infinito, ou seja, deixaria de oscilar — para um sistema massa-mola (m e k) o período de oscilação (T) é dado por — T=2π√m/k — observe nessa expressão que o período desse sistema independe da gravidade local — assim, nesse ambiente de microgravidade, o período do sistema bloco-mola não sofrerá alteração, já o período do pêndulo simples deixará de ser o mesmo — R- B
16- Novo comprimento ℓ do pêndulo quando a temperatura subir de 10oC — ℓ = ℓo (1 + α(t – to) — ℓ = 10(1 + 10.10-6.10 —
ℓ=1,0001m — cálculo do período T que pelo enunciado vale T= √(4ℓ) — T= √(4.1,0001) — T= 2.√1,0001 s — para meio ciclo de oscilação o período será T=√1,0001 s — se, para cada meia oscilação o período aumenta de T=√1,0001 s, o relógio irá atrasar — R- C
17- A — amplitude do pêndulo — T — período do pêndulo — T=2π√ℓ/g
01) Falsa — o período de um pêndulo simples é inversamente proporcional à raiz quadrada da gravidade local (g) conforme mostra a expressão — T=2π√ℓ/g
02) Falsa — quadruplicando o comprimento (L) de um pêndulo simples, seu período duplica, pois o período é diretamente proporcional à raiz quadrada do comprimento — veja a equação — T=2π√ℓ/g
04) Falsa — observe na figura baixo a amplitude A, que é definida como sendo a distância máxima (A) (ou o ângulo máximo θ)
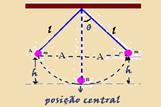
que a partícula se afasta de sua posição de equilíbrio — na posição central, a energia mecânica é igual à energia cinética onde
a velocidade é máxima e a energia potencial é nula — a energia mecânica é constante em todos os pontos (sistema conservativo) e, na posição central vale Em=Ec + Ep — Em=mv2/2 + 0 — Em=mv2/2 — a velocidade no ponto central é máxima e vale — v=w.A — w=2π/T — v= (2π/T).A — Em=m.v2/2 — Em=m/2.(4π2/T2).A2 — Em=2mπ2.A2/T2 — em todos os pontos a energia mecânica é a mesma e observe na expressão que ela é diretamente proporcional ao quadrado da amplitude A.
09) Verdadeira — veja teoria
16) Verdadeira — veja teoria.
R- (08 + 16) = 24
18- O período T do pêndulo é dado por T=2π√(L/g) — como o relógio está atrasando seu período é maior do que deveria ser e assim, seu comprimento deve ser reduzido com o ajuste da porca sendo para a direita — se, para um dia (1.440min) o relógio atrasa 1 min, então o pêndulo deve registrar um tempo de 1.439min — ∆t=natraso.Tatraso=ncorreto.Tcorreto — 1439Tatraso=1.440Tcorreto — 1439. 2π√(Latraso/g) =1.440. 2π√(Lcorreto/g) — Lcorreto/Latraso=(1.439/1.440)2 — Lcorreto/35 = 0,9986 — Lcorreto=34,95cm —
∆L=35 – 34,95=0,05cm=0,5mm — como cada rotação provoca variação de 1 mm, para que o relógio funcione corretamente deve ser dada meia rotação à direita — R- C
19-Pêndulo Simples – consta de uma massa m, presa na extremidade inferior de um fio ideal, fixada verticalmente na sua extremidade superior (figura)
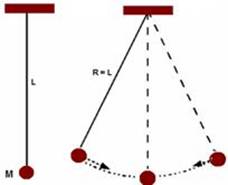
Se o pêndulo simples oscilar, com oscilações de pequena abertura (no máximo 15o), ele descreve um movimento circular de raio R=L, sendo L o comprimento do fio.
Seu período (T), que é o tempo que ele demora para efetuar um “vai e vem” completo é fornecido pela expressão:

Observe nessa expressão que o período T do pêndulo depende da aceleração da gravidade g e do comprimento do pêndulo L — o período de um pêndulo simples é diretamente proporcional à raiz quadrada de seu comprimento L — assim, para dobrar o período T de um pêndulo, seu comprimento L deve ser quadruplicado e o relógio atrasa — o período de um pêndulo simples é inversamente proporcional à raiz quadrada da aceleração da gravidade g — assim, quanto maior for a aceleração da gravidade do local onde está o pêndulo, menor será o seu período e o relógio adianta — uma das aplicações do pêndulo simples é a determinação da aceleração da gravidade — período ao nível do mar — To=2π√(Lo/go) — período numa grande altura — Th==2π√(Lh/gh) — para que ele funcione bem nos dois locais — To = Th — =2π√(Lo/go) =2π√(Lh/gh) — Lo/go = Lh/gh.
• Lo/go = Lh/gh — Lo/Lh =gh/go — comprimento ao nível do mar (Lo) — comprimento na altitude h (Lh=Lo(1 + α.∆t) — Lo/[(Lo(1 + α.∆t)] = go/gh — 1/(1 + α.∆t) = go/gh — go + go.α.∆t = gh — α = (gh – go)/go. ∆t.
