Função horária da elongação do MHS – Resolução
Resolução comentada dos exercícios de vestibulares sobre
função horária da elongação do MHS
1-
a) T=2s — f =1/T — f= 1/2Hz (percorre meia volta em cada 1s)
b) w=2p/T — w=2p/2 — w=prad/s (varre um ângulo de prad em cada 1s)
c) A=4m
d) na posição (elongação) x=0 existem duas fases.
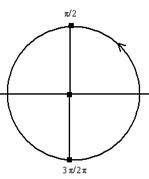
Como ela está se deslocando em 0, para a esquerda, teremos quejo=p/2 rad
e) j = jo + w.t — j = p/2 + p.t
x = A.cosj — x = 4.cos (p/2 + p.t)
f)
t=0 — x=4cos(p/2 + p.t) — x=4cos (p/2 + p.0) — x=4cos (p/2) — x=4.0 — x=0
t=0,5s — x=4cos (p/2 + p.t) — x=4cos (p/2 + p.0,5) — x=4cos (p) — x=4.(-1) — x= -4m
t=1s — x=4cos (p/2 + p.t) — x=4cos (p/2 + p.1) — x=4cos (3p/2) — x=4.0 — x=0
t=1,5s — x=4cos (p/2 + p.t) — x=4cos (p/2 + p.1,5) — x=4cos (2p) — x=4.(+1) — x= +4m
t=2s — x=4cos (p/2 + p.t) — x=4cos (p/2 + p.2) — x=4cos (5p/2) — x=4.0 — x=0
t=4,5s — x=4cos (p/2 + p.t) — x=4cos (p/2 + p.4,5) — x=4cos (5p) — x=4.(-1) — x= -4m
g)
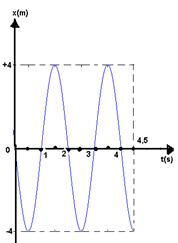
02-
a) w=2p/T = 2pf — 2p = 2pf — f = 1Hz
b) Para que DB e CD sejam pontos médios de AD e A’D, os ângulos estão indicados na figura abaixo
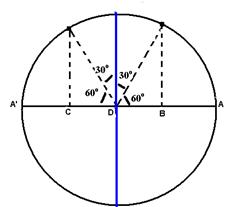
Para se deslocar de B a C o ponto P deve varrer um ângulo de 30o + 30o = 60o = p/3 rad.
Dj= p/3rad w=Dj/Dt — 2p = p/3/Dt — Dt = 1/6s
w= 2prad/s
03-
A = 2m
T = 4s — w=2p/T — w=2p/4 — w = p/2 rad/s
Quando x=0, Wo pode ser p/2 rad ou 3p/2. Observando o gráfico verificamos que é p/2, pois, quando t=1s — A = -2m
04- B
05-
T1 = 1,5s — f1 = 1/1,5Hz T2 = 6s — f2 = 1/6 Hz
F1 / f2 = 1/1,5 X1/6 — f1/f2 = 4
06-
a) A=4m —- w=2p/T —- 4p = 2p/T —- T = 1/2s — f=1/T —- f=2Hz
b) Como jo=0, ele partiu do ponto A=+4m
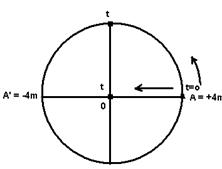
Até chegar a 0, ele demorou um tempo t que é igual a um quarto do período T=0,5s — t=0,5/4 — t = 0,125s
07-
:Cálculo do período T — w=2p/T — p/2 = 2p/T — T = 4s
Para ir de +A até 0 ela andou durante um quarto do período, ou seja, durante t=4/4 — t=1s
08-
O período é T=4s —– w=2p/T —- w= 2p/4 —- w=p/2rad/s e A=2m
Quando x=1m — t=0 — x=Acos(wt+q) — 1=2cos(w.0 +q) —- 1=2cosq —- cosq=1/2 —- q=60o=p/3
x=Acos(wt+q) —- x=2cos(p/2+p/3)
09-
a) V=DS/Dt —- V=26/13 —- V=2cm/s
b) f1=1/2Hz —- f2=1/8Hz —- f1/f2=1/2X8/1 —- f1/f2=4
10-
A=6m —- T=8s —- w=2p/T —- w=2p/8 —- w=p/4rad/s
Quando x=0, a partícula está na posição angular inicial p/2 rad ou 3p/2 rad. Se o MCU for no sentido anti-horário, observando o gráfico verificamos que jo=3p/2 rad.
X = A.cos(jo+ wt) —- x=6.cos(3p/2 + p/4.t)
11- Função horária para o MHS — x = a.cos(Φo+ω.t) — ω =2π/T — T (período) — x1=a.cos {(π/12) + (3π/4).t} —
X2=a.cos {(3π/4).t} — como oscilam de modo idêntico a amplitude e o período são os mesmos para as duas partículas —
Quando t=8/9s — x1=a.cos {(π/12) + (3π/4).(8/9)} — x1=a.cos(3π/4) — x1=a.√2/2 — X2=a.cos {(3π/4).(8/9)} — x2=a.cos(2π/3) — x2=a/2 — x1 – x2=a√2/2 – a/2 — √2≈1,41 — x1 – x2=0,21.a — R- D
12- Função horária da elongação x de um MHS de amplitude xo e pulsação w — x=xo.cos(wt + фo) — veja o esquema abaixo —

No caso em estudo, em t = 0 a partícula está no ponto de elongação máxima, portanto фo= 0 — quando t=1s — xo – a=xocos(w.1 + 0) — cosw=(xo – a)/xo (I) — quando t=2s — xo – (a + b)=xocos(w.2) — xo – a – b = xo.cos2w —
cos2w=(xo –a – b)/xo II) — cos2w=2.(cos2w) – 1 (III) — (I) e (III) em (II) — 2{(xo– a)/xo}2 – 1 = (xo – a – b)/xo —
2{(xo2 – 2.a.xo + a2)/xo2} = (xo – a – b)/xo + 1 — 2xo2 – axo – bxo = 2xo2 – 4axo + 2.a2 — (4ª – a – b).xo = 2.a2 —
xo=2.a2/(3.a – b) — R- C
13-
Num MHS a posição angular x varia com o tempo conforme a função x = A.cos(φo + wt) que é a função horária da elongação e onde x é a elongação; w, a pulsação ou freqüência angular ou ainda velocidade angular; A, a amplitude (elongação máxima) e φo a fase inicial da partícula em MHS.
I. Correta — compare x(t) = 4.cos[(π/2)t + π] com x = A.cos(φo + wt) e verifique que a amplitude A=4m.
II. Correta — observe que W=π/2rad/s — W=2π/T — π/2=2π/T — T=4s.
III. Correta — f=1/T=1/4=0,25Hz.
R- E.
14-
I. Falsa — Elongação (x) – posição (localização) da partícula em MHS sobre o eixo x em relação à origem 0, ou seja,
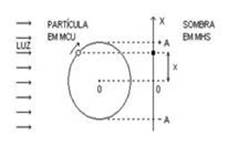
mostra a que distância de 0 a partícula se encontra em determinado instante.
II. Falsa — Amplitude (A) – em módulo é a elongação máxima do MHS e corresponde ao raio da circunferência do
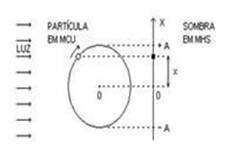
MCU (R=A).
III. Falsa — O MHS não é qualquer movimento vibratório — nele o móvel se desloca sobre a mesma trajetória, indo
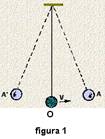
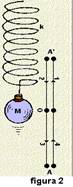
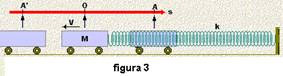

e vindo, em relação a uma posição média de equilíbrio (ponto O, onde a resultante das forças que agem sobre ele é nula)
IV. Falsa — ela varia de acordo com a função — a= -w2.A.cos(φo + w.t) função horária da aceleração do MHS
Observe que:
* quando x=0 — a=0
* quando x= +A — a= -w2A — valor mínimo de a, pois φ=π rad e cos π= -1 — amínimo= – w2.A
* quando x= -A — a= w2A — valor máximo de a, pois φ=2π rad e cos 2π= 1 — amáximo = w2.A
V. Correta — Período (T) – corresponde ao tempo que o MCU demora para efetuar uma volta completa ou ao tempo que o MHS demora para efetuar um “vai e vem” completo sobre a reta x — observe, pela definição, que ele independe da amplitude A do MHS.
R- E.
