Função horária da velocidade e da aceleração do MHS – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Função horária da velocidade e da aceleração do MHS
1-
a) A=4m w=prad/s jo=prad
v= -wAsen(jo + wt) — v= -p.4.sen(p + pt) — v= – 4p.sen(p + pt)
b) v maxima — vmáxima= w.A — vmáxima= p.4 — vmáximo= +4pm/s
v mínima — vmínima= -w.A — vmínima= -p.4 — vmínima= – 4pm/s
c)
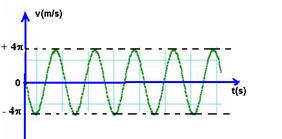
d) a= -w2.A.cos(jo + wt) — a= -p2.4.cos(p + pt) — a= -4p2.cos(p + pt)
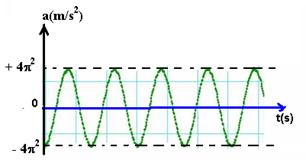
e) aceleração máxima — amáxima= w2A — amáxima= +4p2 m/s2
aceleração mínima — amínima= – w2A — amínima= – 4p2 m/s2
e)
f)
2- C
3-
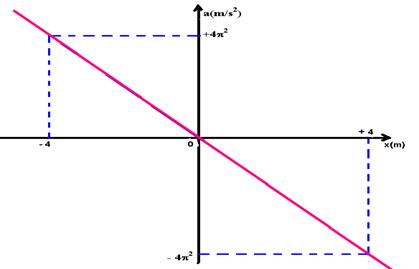
a= -w2Acosj — qdo x=A= 1 — j=p — a= 4 — 4 = -w2.(1).cosp — 4 = -w2.(1).(-1) — w = Ö4 — w = 2 rad/s
4- D
5-
R=A=20/2 — R=10cm f=60rpm=60/60 — f=1Hz — T=1s
W=2p/T — w=2p/1 — w=2p rad/s
V é máxima quando j=3p/2, sendo sen3p/2= – 1 — v= -w.A.senj — v= -w.10.sen3p/2 — v= -2p.10.(-1)
Vmax = 20p cm/s
6-
Vmáxima=2pm/s —- A=20cm=0,2m
Vmáxima= w.A — 2p=w.0,2 — w=10prad/s — w=2p/T — 10p=2p/T — T=0,2s
7-
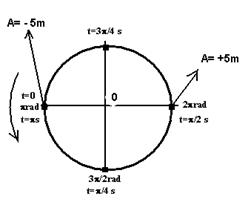
a) vo=0 (vide gráfico)
Como v=0 nos extremos, sua fase inicial ou é zero ou prad e observando o gráfico verificamos que jo=prad
b) T=ps (veja gráfico) — w=2p/T — w=2p/p — w=2rad/s
vmáximo=10m/s (veja gráfico) — vmáximo=wA — 10=2A — A=5m
c) é a amplitude, ou seja, 5m
d) amáxima=w2.A — amáxima=22.5 — amáxima=20m/s2
8-
Quando o carrinho se choca com a mola, o módulo de Vo é máximo e vale vmáximo=w.A — Vo=w.A — Vo=2p/T.A —
T=2pA/Vo
9-
a) Observe pelo gráfico que o período do movimento vale T=0,2s. Como a freqüência f é o inverso do período T, temos f=1/T
— f=1/0,2 — f=5Hz.
A amplitude á a distância da origem ao ponto máximo. Logo, A=0,1m
Pulsação – ou velocidade angular — w=2p/T — w=2p/0,2 — w=10prad/s.
b) Equação da elongação ou da posição, na vertical é y=-Acos(jo + wt) — y= .0,1.cos(0 + 10pt) — y= 0,1cos10p
jo=0, pois, quando t=o, A=+0,1m (elongação máxima).
10-
a) A=7cm — w=p/2rad/s — w=2p/T — p/2=2p/T — T=4s
Para que o móvel vá da posição de equilíbrio até o ponto de elongação máxima, ele se move durante 1/4 de seu período, que é de 4s (tempo que demora para efetuar uma volta completa) — t=T/4 — t=4/4 — t=1s
b) vmáxima=w.A=p/2.7 — vmáxima=3,5pcm/s
amáxima=w2.A — amáxima=(p/2)2.7 — amáxima=1,75p2cm/s2
11- E
12- a) O gráfico fornece a posição da peça em função do tempo — o período é o intervalo de tempo para que a situação cinemática se repete — observe que isso ocorre a cada 4s — portanto T=4s — a frequência é o inverso do período — f=1/T=1/4 — f=0,25 Hz
b) A velocidade da peça é nula nos instantes em que a elongação é máxima ou mínima, quando ocorre inversão no sentido do movimento, ou seja: t = 1 s; t = 3 s e t = 5 s.
c) Os instantes em que a aceleração da peça é máxima (em módulo) são os instantes em a força elástica tem intensidade máxima. Como F = k |x|, a força é máxima onde a elongação é máxima ou mínima, ou seja: t = 1 s; t = 3 s e t = 5 s.
